Цели
работы:
Исследовать
свойства
преобразования
Фурье
для
дискретных
сигналов.
Задачи
работы:
1.
Изучение
процессов
и
особенностей
применения
ДПФ
к
дискретным
сигналам.
2.
Изучение
свойств
ДПФ
на практике.
3.
Научиться
применять
инструменты
программного
пакета
MatLab
для
ДПФ.
4.
Ознакомиться
с
модулем
SpTool
Краткий
конспект
теоретической
части
Теорема
Фурье
Дискретное
Преобразование
Фурье
Свойства
ДПФ
Быстрое
преобразование
Фурье
дата
Оценка
(max
5)
Бонус
за
сложность
подпись














«Дискретное преобразование Фурье»
В
таблице
1
представлены
функции
MatLab,
используемые
для
работы
с
ДПФ.
Таблица
1
–
Функции
Matlab
для
работы с
ДПФ
производится
для каждого
столбца
в
N
обычно
задается
как 2 в некоторой
В
результате
применения
функции
fft
получим
комплексную
составляющую
спектра
исходного
сигнала,
представленную
в
алгебраической
форме.
По
составляющим
вектора
X
спектра.
можно
определить
модуль,
отдельно
действительную
и
отдельно
мнимую
составляющие
Задание:
разработать
скрипт
для
построения
действительной
и
мнимой
составляющей
сигнала
и
Вашему
варианту.
графиков
анализируемого
сигнала,
график
модуля
гармоник
согласно
N=8; %Количество
отсчетов. n=0:1:7; %Индексы
отсчетов. t=1/8000; %Частота
дискретизации.
x=sin(2*pi*1000*n*t)+0.5*sin(2*pi*2000*n*t+3*pi/4);%Входной
сигнал.
figure(1)
plot(x),grid
on %График анализируемого сигнала.
y=fft(x) %Преобразование Фурье.
figure(2) %График
действительной составляющей.
stem(real(y)),grid
on
figure(3)
stem(imag(y)),grid
on %График
мнимой составляющей.
Xm=abs(y)
figure(4) %График
модуля гармоник. stem(Xm),grid
on
Xmm=2*abs(y)/N
figure(5)
stem(Xmm),grid
on %График
модуля гармоник (нормированный).
(вклейте
разработанную
Вами
программу)
y
= fft(x)
Вычисляет
прямое
ДПФ
для вектора
X
;
если
X
-матрица,
то преобразование
отдельности
y
= fft(x, N)
Предварительно
приводит
данные
к
размеру
N
,
урезая
их
или
дополняя
нулями.
Размер
степени.
x
= ifft(y)
x
= ifft(y, N)
аналогичные
команды
для вызова
функции
обратного
ДПФ.

















1. Дискретное преобразование Фурье в программном пакете MatLab
Функция
Описание
Вклейте
полученные
графики
в
соответствующие
поля:
Рисунок
1
–
Исходная
последовательность
Рисунок
2
–
Действительная
часть
ДПФ
Рисунок
3
–
Мнимая
часть
ДПФ
Рисунок
4
–
Ненормированный
модуль
ДПФ
Рисунок
5
–
нормированный
модуль
ДПФ




Выводы:
Если
входной
сигнал
содержит
компонент
с
некоторой
промежуточной
частотой,
лежащий
между
аналитическими
частотами
mf
s
N
,
то
этот
входной
сигнал
проявится
в
некоторой
степени
на
всех
N
частотах,
на
всех
отсчѐтах.
Задание:
разработать
код
m-файла,
результатом
выполнения
которого
являются
графики
выходного
спектра
для
заданной
частоты
и
частоты,
увеличенной
на
10%
согласно
Вашему
варианту
задания.
N=8; %Количество
отсчетов.
n=0:1:7; %Индексы
отсчетов.
t=1/8000; %Частота
дискретизации.
x=sin(2*pi*2200*n*t); %Анализируемый
сигнал.
y=fft(x); %Преобразование
Фурье
в
диапазоне
0-(N-1).
xp=fftshift(y) %Преобразование
Фурье
в
диапазоне
(–N/2)-(N/2-1).
f=-N/2:1:(N/2-1)
a=abs(xp)/4 %Нормированный
модуль в
диапазоне
(–N/2)-(N/2-1).
figure(1) %График
нормированного
модуля
stem(f,a),grid
on %в
диапазоне
(–N/2)-(N/2-1).
x2=sin(2*pi*2500*n*t);
%Анализируемый
сигнал.
y2=fft(x2); %Преобразование
Фурье
в
диапазоне
0-(N-1).
xp2=fftshift(y2) %Преобразование
Фурье
в
диапазоне
(–N/2)-(N/2-1).
a2=abs(xp2)/4 %Преобразование
Фурье
в
диапазоне
(–N/2)-(N/2-1).
figure(2) %График
нормированного
модуля
stem(f,a2),grid
on %в
диапазоне
(–N/2)-(N/2-1).
(вклейте
разработанную
Вами
программу)









Вклейте
результаты
выполнения
скрипта:
Выводы:
Рисунок
6
–
Спектр
входной
последовательности
для
частоты
Гц
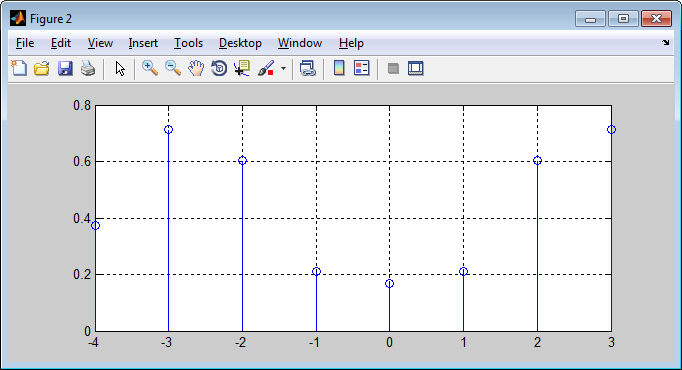
Рисунок
7
–
Спектр
входной
последовательности
для
частоты
Гц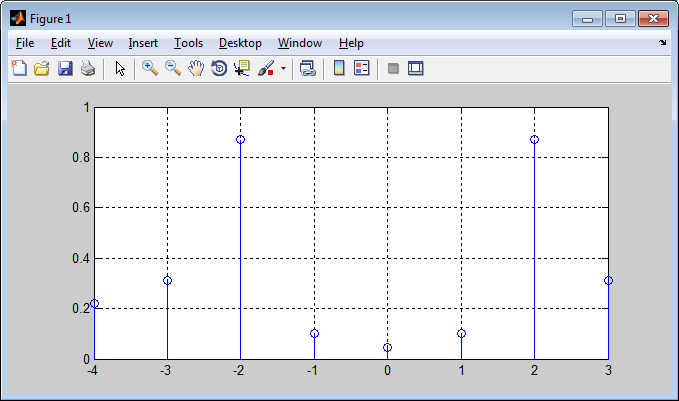






Эффект
растекания
спектра
При ДПФ мы предполагали (умалчивая), что последовательность отсчетов
анализируемого
сигнала
является
периодически
продолженной
вперед
и
назад
во
времени.
При
этом,
если
значения
начальных
и
конечных
отсчетов
сигнала
сильно
отличаются,
при
периодическом
повторении
на
стыках
сегментов
возникают
скачки,
из-за
которых
спектр
сигнал
расширяется.
Задание:
разработать
скрипт
для
построения
характеристик
кратной
гармонике
согласно
вашему
варианту.
на
частоте,
кратной
и
не
Вклейте
результаты
выполнения
скрипта:
Выводы:
Рисунок
8
–
Спектр
сигнала
для
частоты _Гц
N=32;
n=0:1:31; t=1/32000;
x=sin(2*pi*8000*n*t);
y=fft(x); xp=fftshift(y)
f=-N/2:1:(N/2-1)
a=abs(xp)/16 figure(1) stem(f,a),grid
on
x2=sin(2*pi*8500*n*t);
y2=fft(x2); xp2=fftshift(y2) a2=abs(xp2)/16 figure(2)
stem(f,a2),grid
on
(вклейте
разработанную
Вами
программу)








Выводы:
Рисунок
9
–
Спектр
сигнала
для
частоты
8500_Гц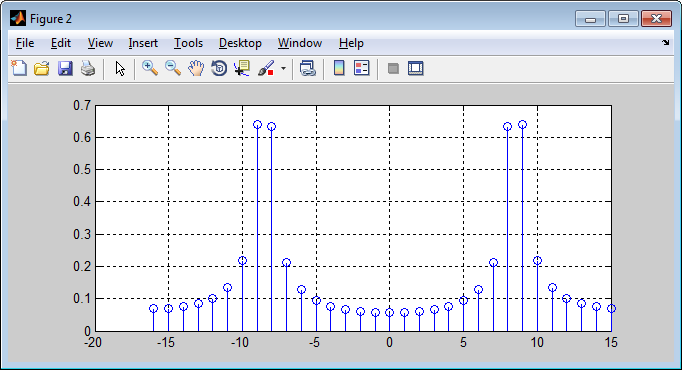

N=5;
fs=100;
t=-1:1/fs:1-1/fs;
nh=(1:N)*2-1;
y=cos(2*pi*nh'*t/T);
Am=2/pi./nh;
Am(2:2:end)=-Am(2:2:end);
s1=y.*repmat(Am',1,length(t));
s2=cumsum(s1);
for
k=1:N
subplot(2,2,k) plot(t,
s2(k,:))
end
Спектр
меандра
Меандр
–
это
последовательность
прямоугольных
импульсов
со
скважностью,
равной
двум.
В
спектре
меандра
присутствуют
только
нечетные
гармоники:
2
A
2
2
2
A
1
1
s(t
)
2
cos t
cos
3
t
cos
5
t
T
3
T
5
T
Гармоники,
образующие
меандр
имеют
амплитуду,
обратно
пропорциональную
номеру
соответствующей
гармоники.
Задание:
разработать
код
m-файла,
результатом
выполнения
которого
являются
графики
меандра,
реализованные
с
различным
количеством
гармоник
(1,2,…,
10,
25,
100
и
др.)















Вклейте
результаты
выполнения
скрипта:
Рисунок
10
–
Графики
меандра,
содержащего
различное
число
гармоник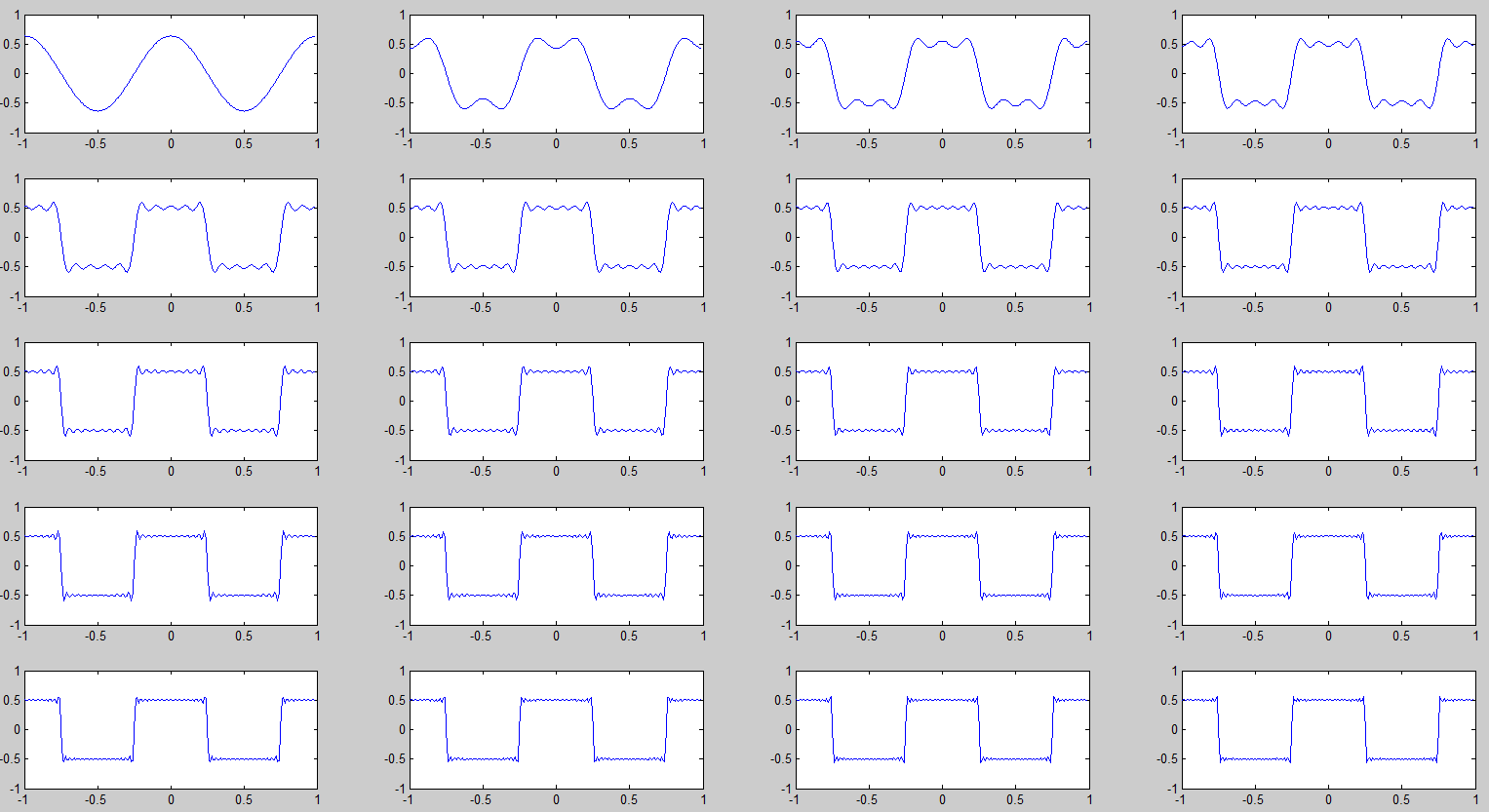

Функции
Matlab,
использованные
в
примере
Функция
sum(X)
в
случае
одномерного
массива
возвращает
сумму
элементов
массива;
в случае
двумерного
массива
-
это
вектор-строка,
содержащая
суммы
элементов
каждого
столбца.
Функция
cumsum(X),
кроме
того,
возвращает
все
промежуточные
результаты
суммирования.
Пример:
Рассмотрим
массив
M:
M
=
8
3
4
1
5
9
6
7
2
Результаты
выполнения
функций:
Функция
repmat(A,M,N)
-
формирование
массива
из
частей
-
использует
преимущество
векторизации.
Она
имеет
три
входных
аргумента:
массив
A,
количество
строк
М
и
столбцов
N
для
вновь
создаваемого
массива.
Функция
repmat
возвращает
массив
B
,
который
использует
массив
A
в
качестве
основы
для
построения
блочной
матрицы
с
количеством
блоков
MxN.
Пример:
A
=
[1
2 3; 4 5 6];
B
=
repmat(A,
2,
3);
Результаты
выполнения
функции:
B
=
1
4
1
4
2
5
2
5
3
6
3
6
1
4
1
4
2
5
2
5
3
6
3
6
1
4
1
4
2
5
2
5
3
6
3
6
Выводы:
cumsum(M)
sum(M)
8 1 6
11
6 13
15
15
15
15
15
15













Задание:
разработать
скрипт
Matlab,
результатом
которого
являются
графики
ДПФ
меандра
при
использовании
различного
количества
гармоник.
(вклейте
разработанную
Вами
программу)

Вклейте
результаты
выполнения
скрипта:
Выводы:
Рисунок
11
– Графики
спектра
меандров
с
различным
числом
гармоник
Использование
GUI
SpTool
В
пакете
Signal
Processing
Toolbox
предусмотрен
графический
интерфейс
пользователя,
облегчающий
его
работу.
Рассмотрим
применение
SpTool
для
решения
задач
анализа.
Для запуска
используется
команда
sptool.
Рисунок
12
–
Главное
окно
SpTool
Главное
окно
разделено
на
3
части:
Сигналы
(Signals),
Фильтры
(Filters),
Спектры
(Spectra).
Для
загрузки
сигнала
в
GUI
используется
пункт
меню
File/Import…
1.
Выбрать
источник
сигнала
(Source):
из
рабочей
области
или
с
диска.
Если
выбран
импорт
из
рабочей
области,
то
в
поле
Workspace
Contents
будет
отображено
текущее
содержимое
рабочей
обалсти.
Далее
в
поле
Import
As…
указываем,
что
переменная
будет
импортирована
как
сигнал
(Signal).
2.
3.
Указываем,
какая
переменная
будет
импортирована,
указываем
частоту
дискретизации
(Sampling
Frequency)
или
указываем
какая
переменная
будет
принята
за
fs.
Указываем
имя
импортируемого
сигнала
в
поле
Name.
Нажимаем
OK
4.
5.
Рисунок
13
– Окно
импорта
























Для
удаления
сигнала
(равно
как
и
любого
объекта)
необходимо
выбрать
пункт
меню
Edit/Clear/<Имя
сигнала>.
В
данном
пункте
меню
отображаются
все
выделенные
объекты.
Для просмотра
сигнала
нужно:
1.
Выделить
сигнал
в списке
Signals
2.
Нажать
кнопку
View.
Появиться
Signal
Browser,
работа
в
котором
интуитивно
понятна.
Рисунок
14
– Signal
Browser
SpTool
позволяет
использовать
различные
методы
спектрального
лабораторной
работе
нас
интересует
только
преобразование
Фурье.
анализа.
В
данной
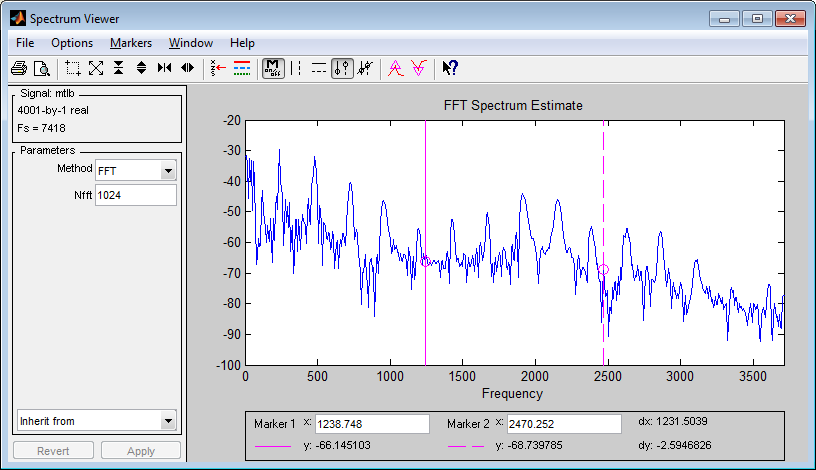
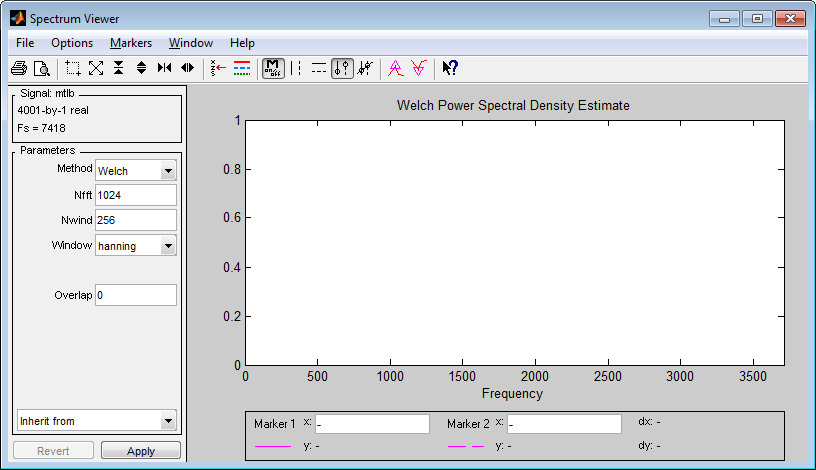
Рисунок
15
–
Просмотр
спектра
сигнала
Для
создание
Фурье-спектра
необходимо:
1.
2.
3.
4.
5.
Выделить
исследуемый
сигнал
в блоке
Signals,
В
блоке
Spectra
нажать
кнопку
Create
В
блоке
Parameters
в поле Method
выбрать
FFT
(БПФ),
В
поле
NFFT
указать
число
точек
FFT.
Нажать
кнопку
Apply.
В
меню
Options
можно
указать
дополнительные
настройки
отображения
спектра.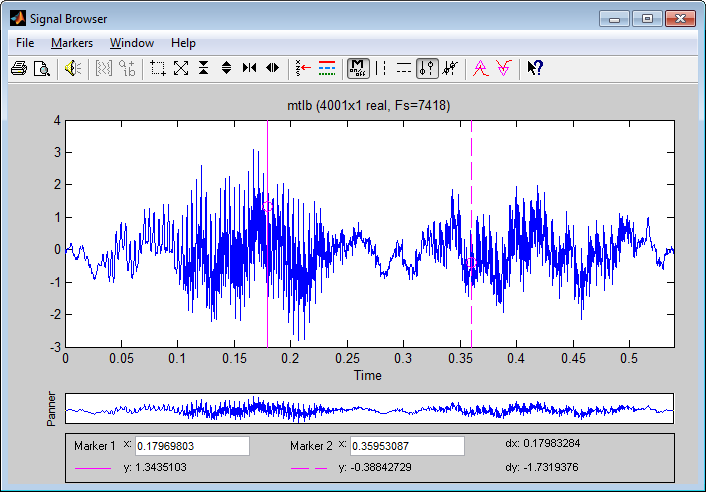









Вклейте
ниже
результаты
работы
с
программой
согласно
Вашему
варианту
задания:
Выводы:
Контрольные
вопросы
1.
2.
3.
4.
5.
6.
Теорема
Фурье.
Что
такое дискретное
преобразование
Фурье?
Назовите
свойства
дискретного
преобразования
Фурье.
Почему
на
практике
используют
быстрое
преобразование
Фурье?
Что такое быстрое
преобразование
Фурье?
Что
такое растекание
спектра?
Рисунок
16
–
Результат
работы с SpTool
Рисунок
17
– Результат
работы с SpTool