
- •Инженерная и компьютерная графика
- •Начертательная геометрия
- •1.1 Задачи начертательной геометрии
- •1.2 Геометрические образы пространства и их обозначения
- •1.3 Метод начертательной геометрии. Виды проецирования
- •1.4 Поверхность как объект пространства
- •1.5 Пересечение поверхности плоскостью
- •1. 6 Взаимное пересечение поверхностей
- •1.6.5 Общий случай пересечения поверхностей вращения.
- •1.6.6 Частные случаи пересечения поверхностей вращения
- •1.7 Преобразование чертежа. Метрические задачи
- •1.7.2 Способ замены плоскостей проекций.
- •1.7.3 Способ вращения вокруг оси, перпендикулярной плоскости проекций
- •1.8 Аксонометрические проекции
- •Пример построения эллипса по двум осям приведен на рис. 1.55
- •1.8.5 Характеристика косоугольной горизонтальной аксонометрической проекции
- •Угол может принимать значения 30, 45 или 60 градусов.
- •1.9 Вопросы для самопроверки по темам первого раздела
- •2 Изображения на чертежах. Виды. Разрезы. Сечения
- •2.2 Виды
- •В табл. 2.1 отражено соответствие названий видов (гост 2.305 -68) плоскостям проекций при прямоугольном проецировании.
- •2.3 Разрезы
- •2.4 Сечения
- •2.5 Выносной элемент
- •2.6 Условности и упрощения при построении изображений
- •2.7 Вопросы для самопроверки
- •Какие изображения на чертежах устанавливает гост 2.305-68?
- •3 Чертежи изделий
- •3.1 Общие сведения о конструкторской документации
- •3.1.1 Понятие об изделии и его составных частях
- •3.1.2 Виды конструкторских документов
- •3.2 Чертежи деталей
- •3.2.1 Общие сведения
- •3.3 Соединения деталей
- •3.4 Чертежи сборочных единиц и их чтение
- •3.5 Вопросы для самопроверки
- •4 Схемы электрические
- •4.1 Общие сведения и основные термины
- •Общие требования к выполнению схем
- •4.3 Схемы электрические структурные (э1)
- •4.4 Схемы электрические функциональные (э2)
- •4.5 Схемы электрические принципиальные (э3)
- •4.6 Общие положения по выполнению схем для изделий вычислительной техники
- •4.7 Перечень вопросов для теоретического собеседования
- •5 Диаграммы функциональных зависимостей
- •5.1 Общие сведения
- •5.2 Оси координат (шкалы) и делительные штрихи
- •5.3 Оформление шкал
- •5.4 Линии в диаграммах
- •6 Схемы алгоритмов и программ
- •6.1 Основные положения
- •6.2 Правила выполнения символов
- •6.3 Правила выполнения линий
- •6.4 Правила выполнения соединений
- •7 Компьютерные технологии выполнения чертежей
- •7.1 Основные положения прикладной компьютерной графики
- •7.2 Графический интерфейс AutoCad
- •7.3 Последовательность освоения функций
- •7.4 Упражнение 1
- •7.4.1 Выполнить геометрические построения отрезков, окружностей и многоугольника, как показано на рис. 7.25. Обозначить точки буквами.
- •7.5 Упражнение 2
- •7.5.1 Начертить два изображения детали (вид сверху и фронтальный разрез), проставить размеры (рис. 7.38).
- •7.5.2.3 Расчленить прямоугольник на отрезки
- •7.5.2.4 Копировать левую вертикальную прямую на 40 мм по оси х, затем - на 65мм
- •8 Оформление чертежей
- •8.1 Форматы чертежей
- •8.2 Основная надпись чертежа
- •Масштабы
- •Надписи на чертежах
- •Основные правила нанесения размеров на чертежах
- •Варианты заданий к разделу 4 «Схемы электрические» лист 1 «Схема электрическая структурная»
- •Варианты заданий к разделу 4 «Схемы электрические» лист 2 «Схема электрическая принципиальная»
- •Варианты заданий к разделу 6
- •Условные изображения соединений на сборочных чертежах
- •Примеры обозначений крепежных изделий
- •Инженерная и компьютерная графика
- •630102, Новосибирск, ул. Кирова, 86
1.6.6 Частные случаи пересечения поверхностей вращения
Пересечение поверхностей, имеющих общую ось.
На рис. 1.38 изображены соосные поверхности. Линия пересечения – окружность, плоскость которой перпендикулярна общей оси вращения.
Пересечение по теореме Монжа
На рис. 1.39.а,б изображены пересечения: а – двух конусов, б – конуса и цилиндра. На рис. 1.40 – двух цилиндров. Во всех случаях обе пересекающиеся поверхности описаны вокруг одной сферы.
Если две поверхности второго порядка описаны около третьей поверхности второго порядка или вписаны в нее, то линия их пересечения представляет собой две кривые второго порядка. Это положение известно в начертательной геометрии как теорема Монжа.
На наглядном изображении пересекающихся цилиндров (рис. 1.40) видны эллипсы – плоские кривые линии пересечения.
Пересечение цилиндрических поверхностей с параллельными осями. Пересечение происходит по прямым линиям – образующим, как показано на рис. 1.41.
а) б)
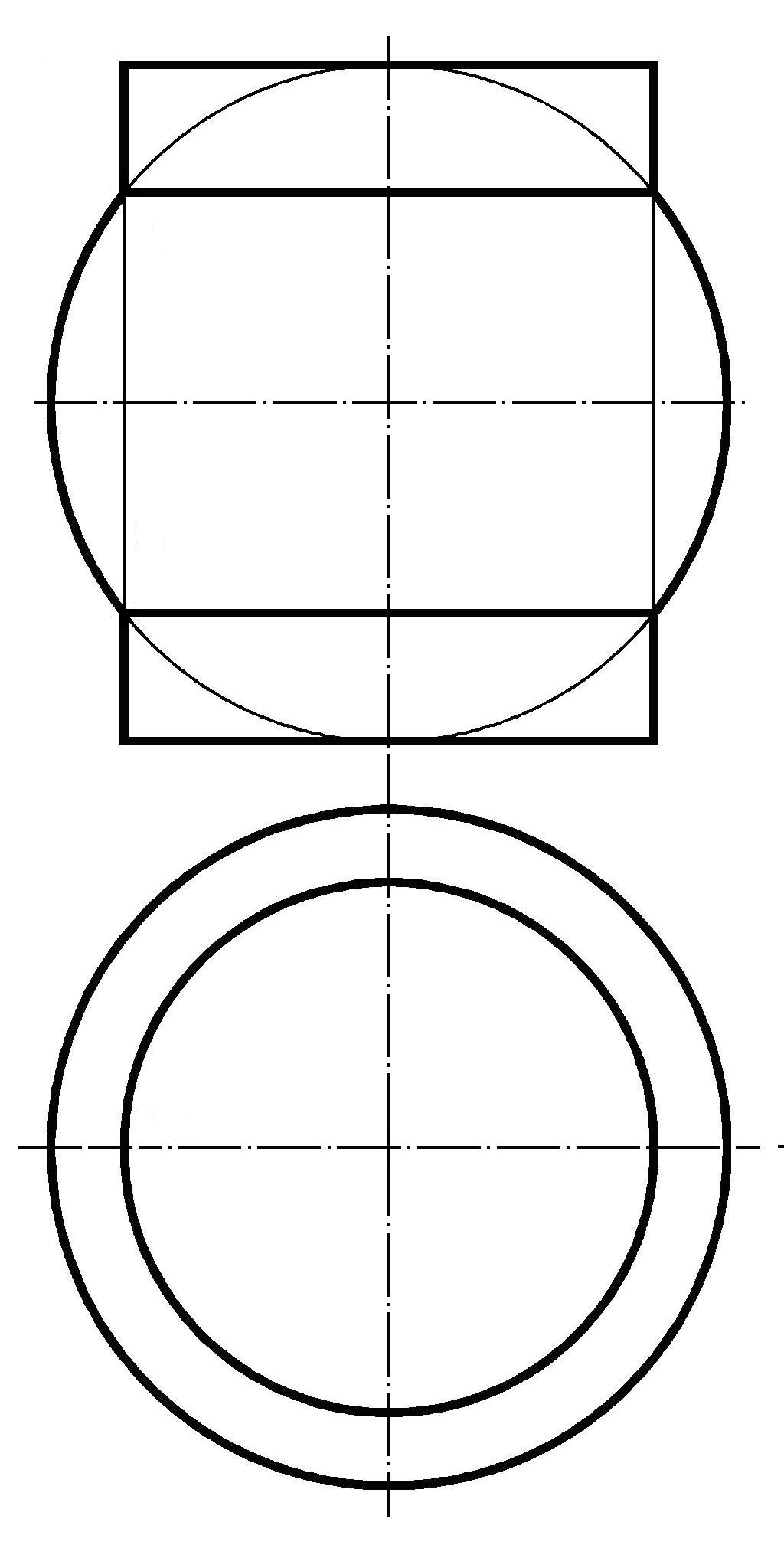
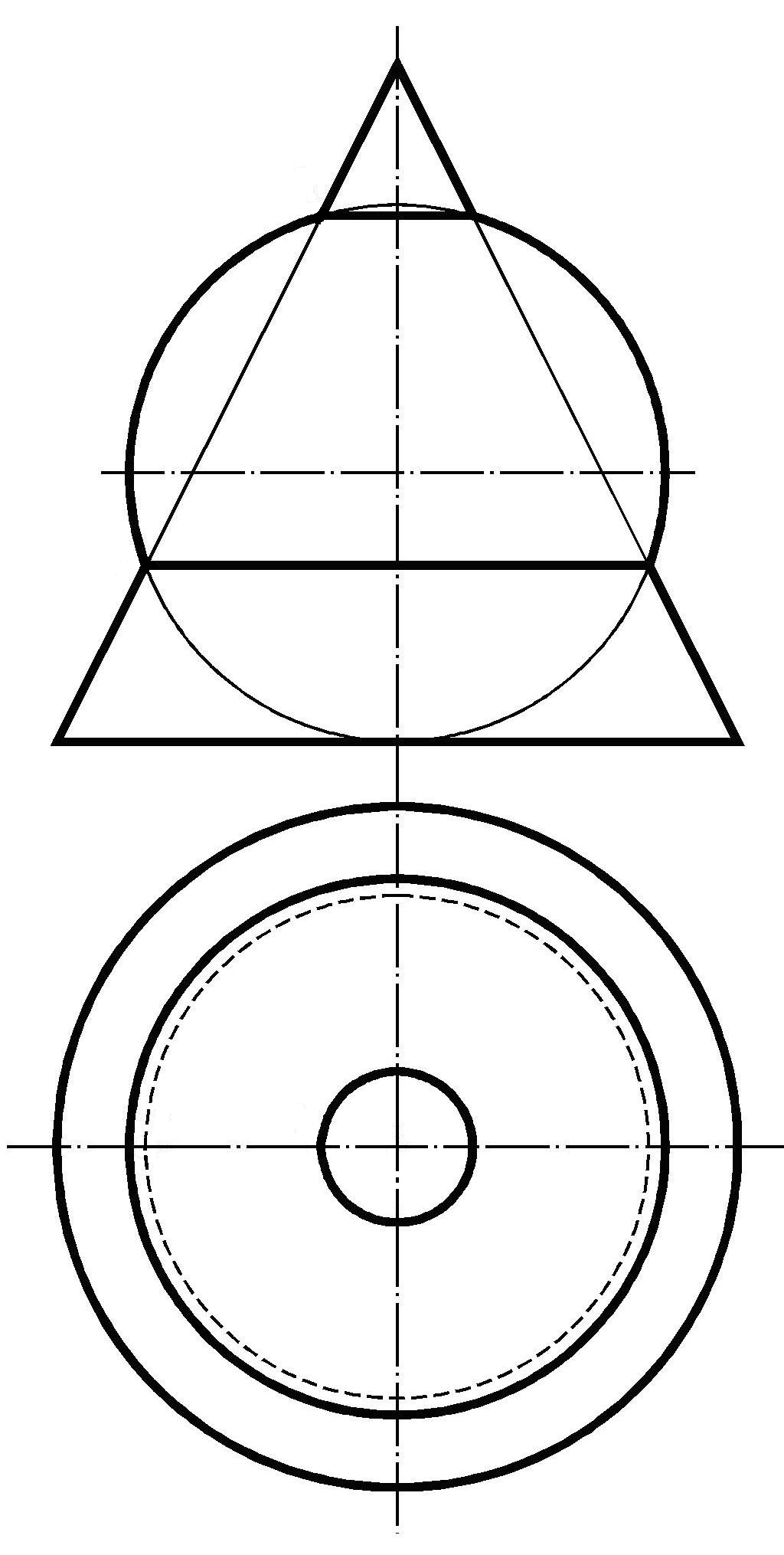
Рис. 1.38 – Соосные поверхности: а - цилиндр и сфера;
б - конус и сфера
а) б)
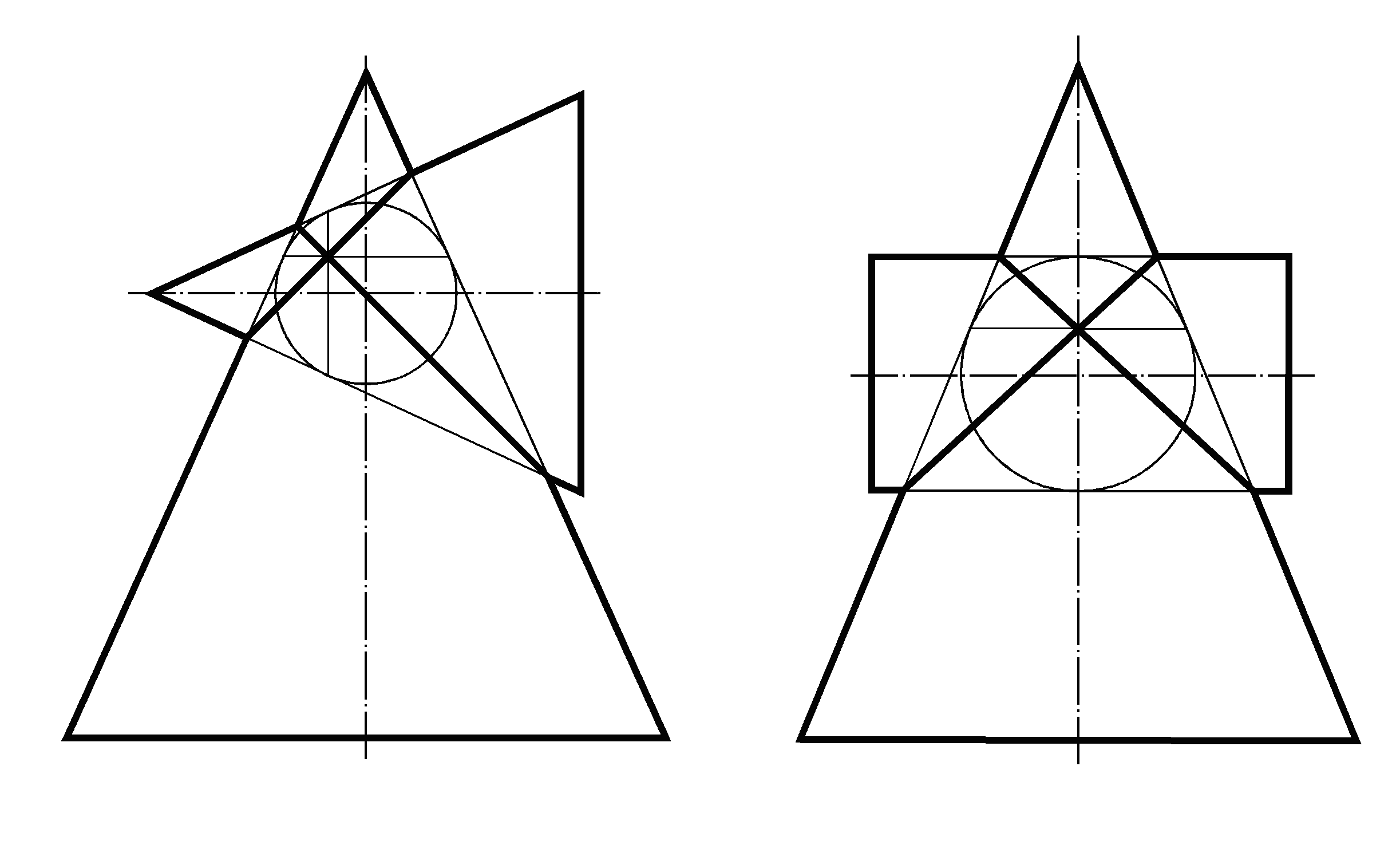
Рис. 1.39 – Примеры взаимного пересечения поверхностей вращения по теореме Монжа:
а - два конуса; б - конус и цилиндр

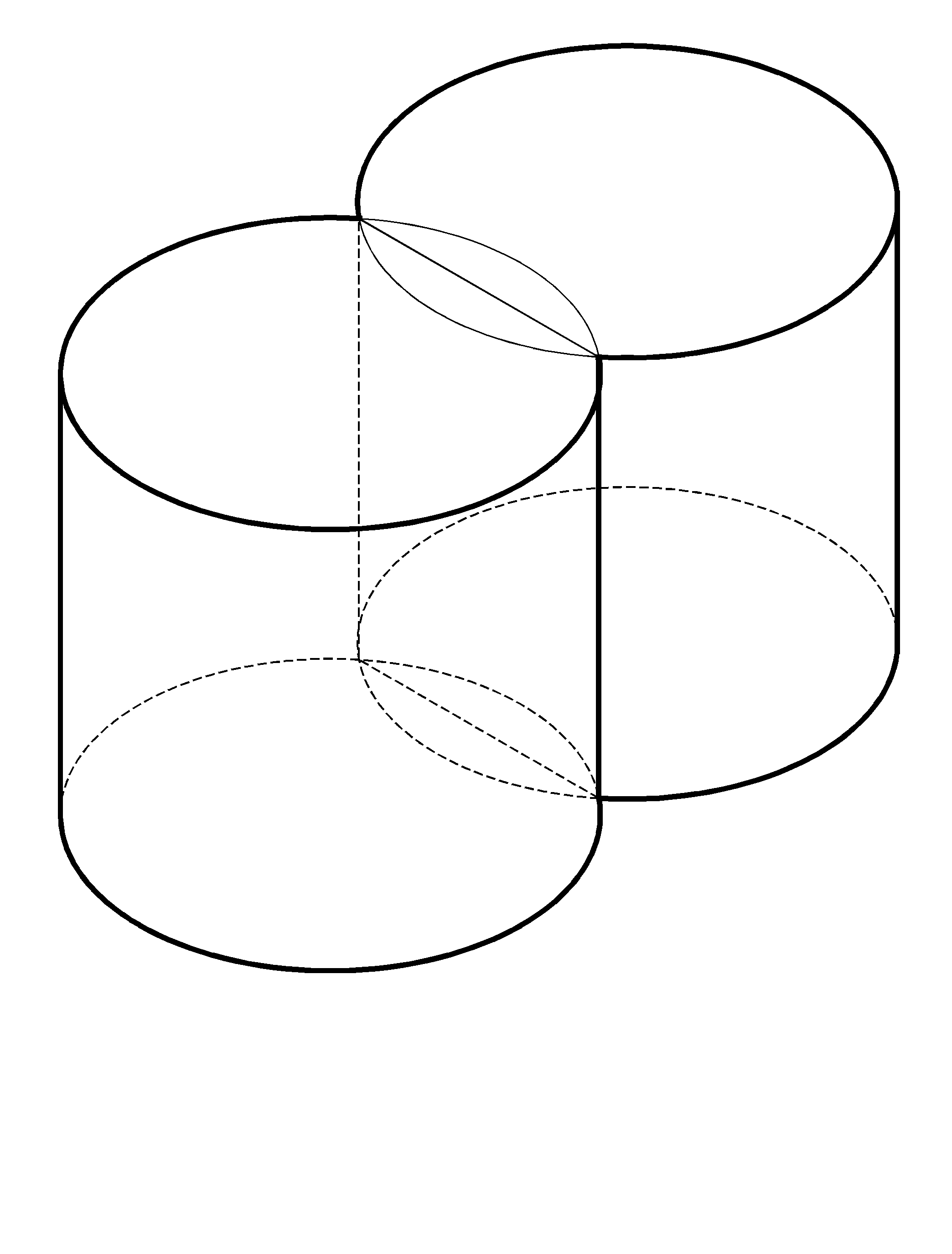
Рис. 1.41 – Взаимное пересечение цилиндров
Рис. 1.40 – Взаимное пересечение двух с параллельными осями
цилиндров по теореме Монжа
1.7 Преобразование чертежа. Метрические задачи
1.7.1 Для упрощения решения позиционных и метрических задач применяют преобразование чертежа. Существуют следующие способы:
способ замены плоскостей проекций
способ вращения вокруг некоторой оси
способ совмещения (вращение вокруг следа плоскости)
способ плоско-параллельного перемещения
В нашем курсе рассмотрим способ замены плоскостей проекций и способ вращения вокруг оси, перпендикулярной плоскости проекций.
1.7.2 Способ замены плоскостей проекций.
Сущность этого способа заключается в том, что объект проецирования (точка, прямая, плоская фигура) не меняет своего положения относительно плоскостей проекций.
Изменяется система плоскостей проекций за счет введения новых, дополнительных плоскостей проекций.
Дополнительные плоскости проекций располагают так, как это удобно для решения задачи.
Замена одной плоскости проекций показана на рис. 1.42,а,б и 1.43.
При решении задач возможна последовательная замена одной, двух и более плоскостей проекций.
Каждая новая плоскость вводится перпендикулярно предыдущей. При этом образуются новые оси проекций: Х14, Х45,…
Линии проекционной связи проводят перпендикулярно новым осям проекций.
а)
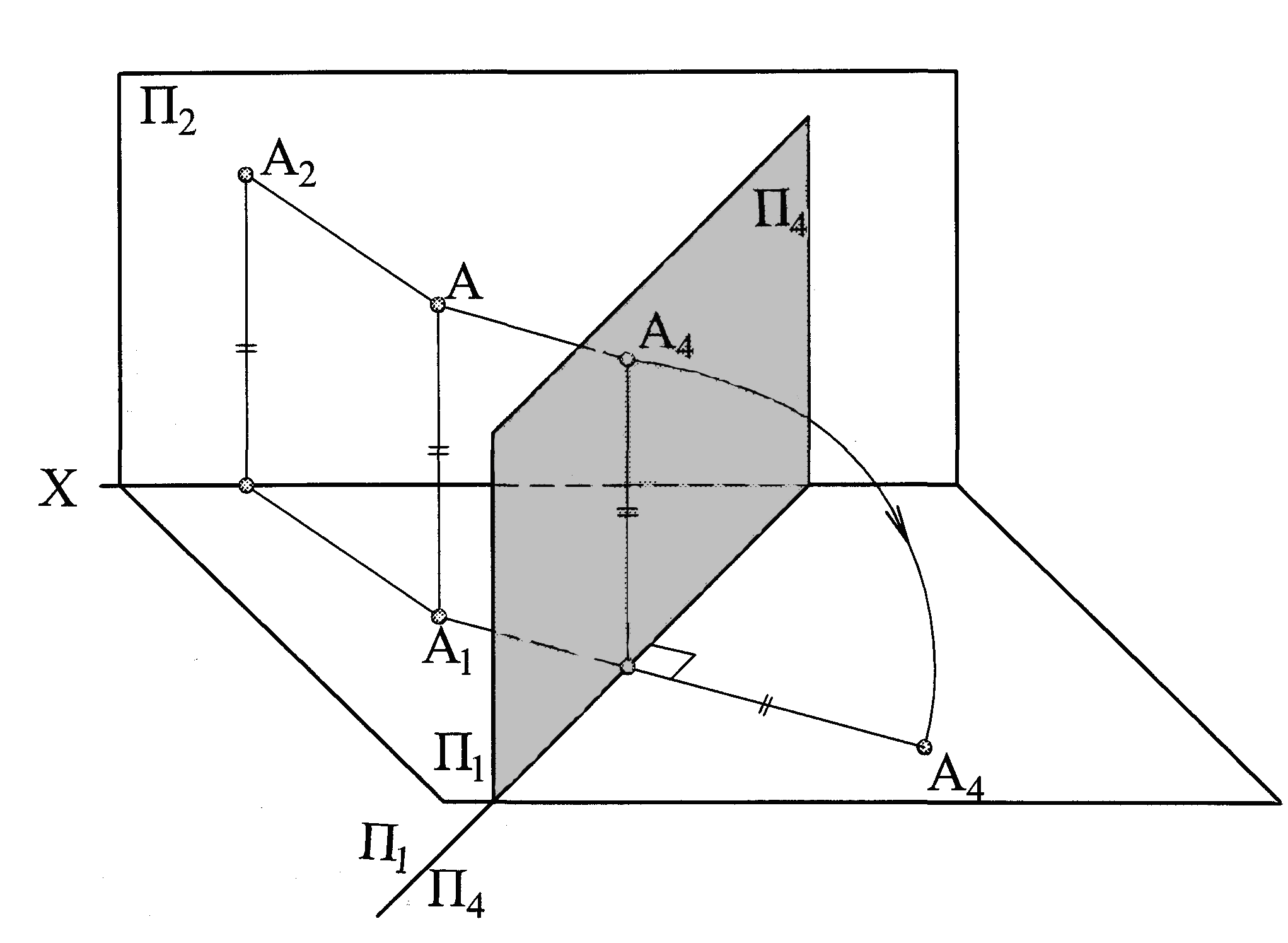
б)

Рис. 1.42 – Способ замены плоскостей проекций на примере проецирования точки А: а - наглядное изображение; б – чертеж.
Новая плоскость проекций П4 введена перпендикулярно П1
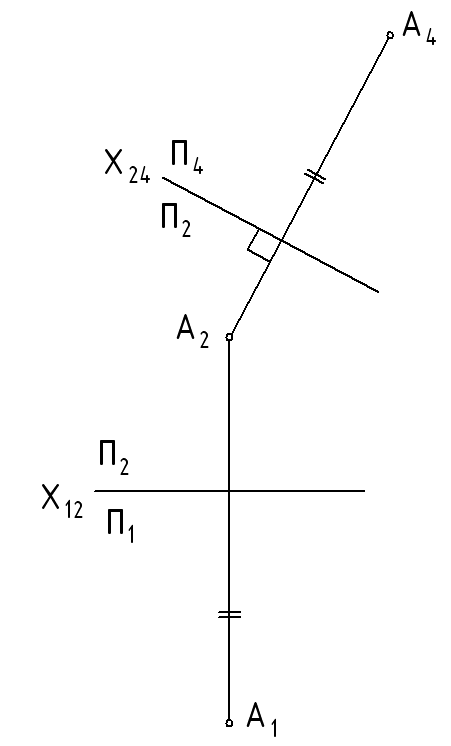
Рис. 1.43 – Способ замены плоскостей проекций.
Новая плоскость проекций П4 введена перпендикулярно П2
Рассмотрим четыре основные задачи способа замены плоскостей проекций.
Задача 1. Преобразовать чертеж прямой общего положения так, чтобы относительно новой плоскости проекций прямая общего положения заняла положение прямой уровня. Условие задачи - рис. 1.44. Прямая общего положения задана отрезком АВ.
( Прямая общего положения не параллельна ни одной плоскости проекций – рис. 1.44.
Прямая уровня - параллельна какой-либо одной плоскости проекций – рис. 1.46)
Решение задачи состоит в том, что новая плоскость вводится параллельно заданной прямой и перпендикулярно П1. Построение видно по чертежу на рис. 1.45. Угол α – истинный угол наклона отрезка АВ к горизонтальной плоскости проекции П1 .
По сути решается две метрические задачи.
Определение натуральной величины отрезка прямой;
Определение угла наклона прямой к горизонтальной плоскости проекций.
Можно ввести новую плоскость перпендикулярно фронтальной плоскости проекций, тогда при натуральной величине отрезка определится угол наклона прямой к плоскости П2.
Задача 2. Преобразовать чертеж прямой уровня так, чтобы относительно новой плоскости проекций прямая уровня заняла проецирующее положение.
(Проецирующей называется прямая, перпендикулярная плоскости проекций - рис. 1.47)
На рис. 1.48 показано решение задачи 2.
Задача 3. Преобразовать чертеж плоскости частного положения так, чтобы относительно новой плоскости проекций она заняла положение плоскости уровня.
Решение задачи представлено на рис. 1.49. Таким образом определяется истинная величина плоской фигуры, занимающей в основной системе плоскостей проекций проецирующее положение.
На основе этой задачи выполняется построение дополнительных видов, наклонных разрезов и сечений по правилам ГОСТ 2.305-68 (раздел 2).
а)

б)

Рис. 1.44 – Прямая общего положения: а - наглядное изображение,
б - чертеж
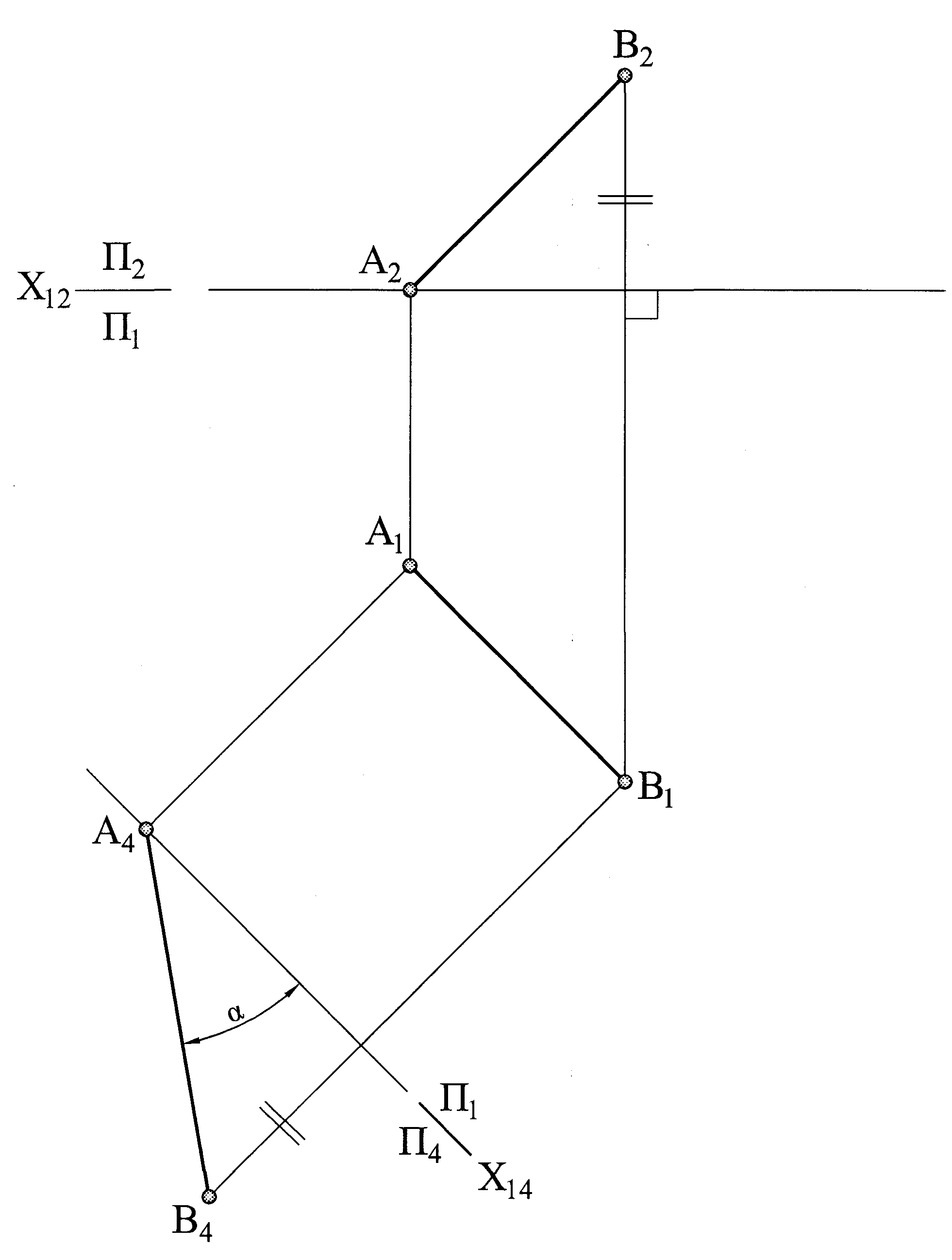
Рис. 1.45 – Построение натуральной величины отрезка способом замены плоскостей проекций
а)
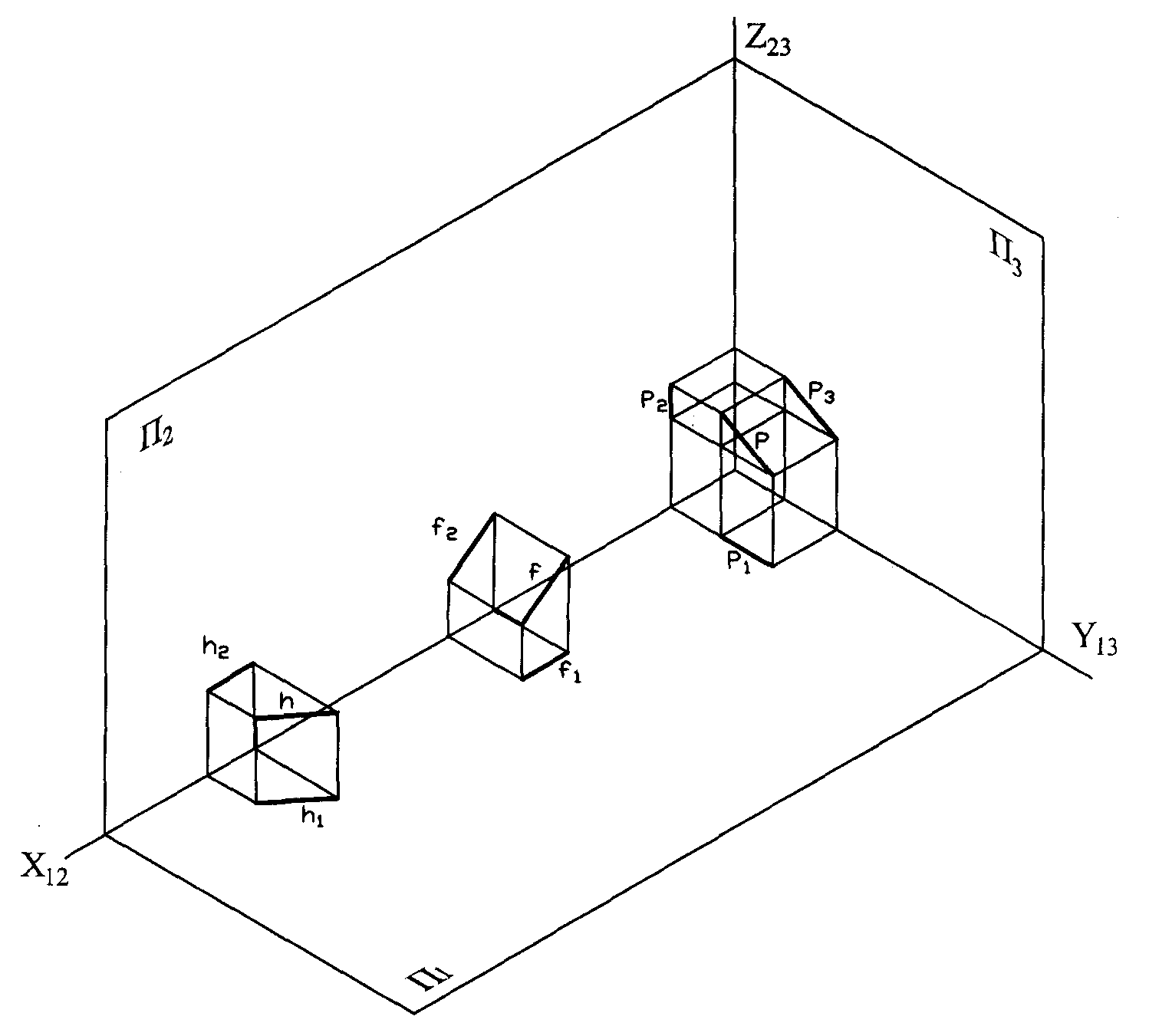
h – прямая f – прямая p – прямая
горизонтального фронтального профильного
уровня уровня уровня
б)

Рис. 1.46 – Прямые уровня: а - наглядное изображение;
б - чертеж
а)
б)
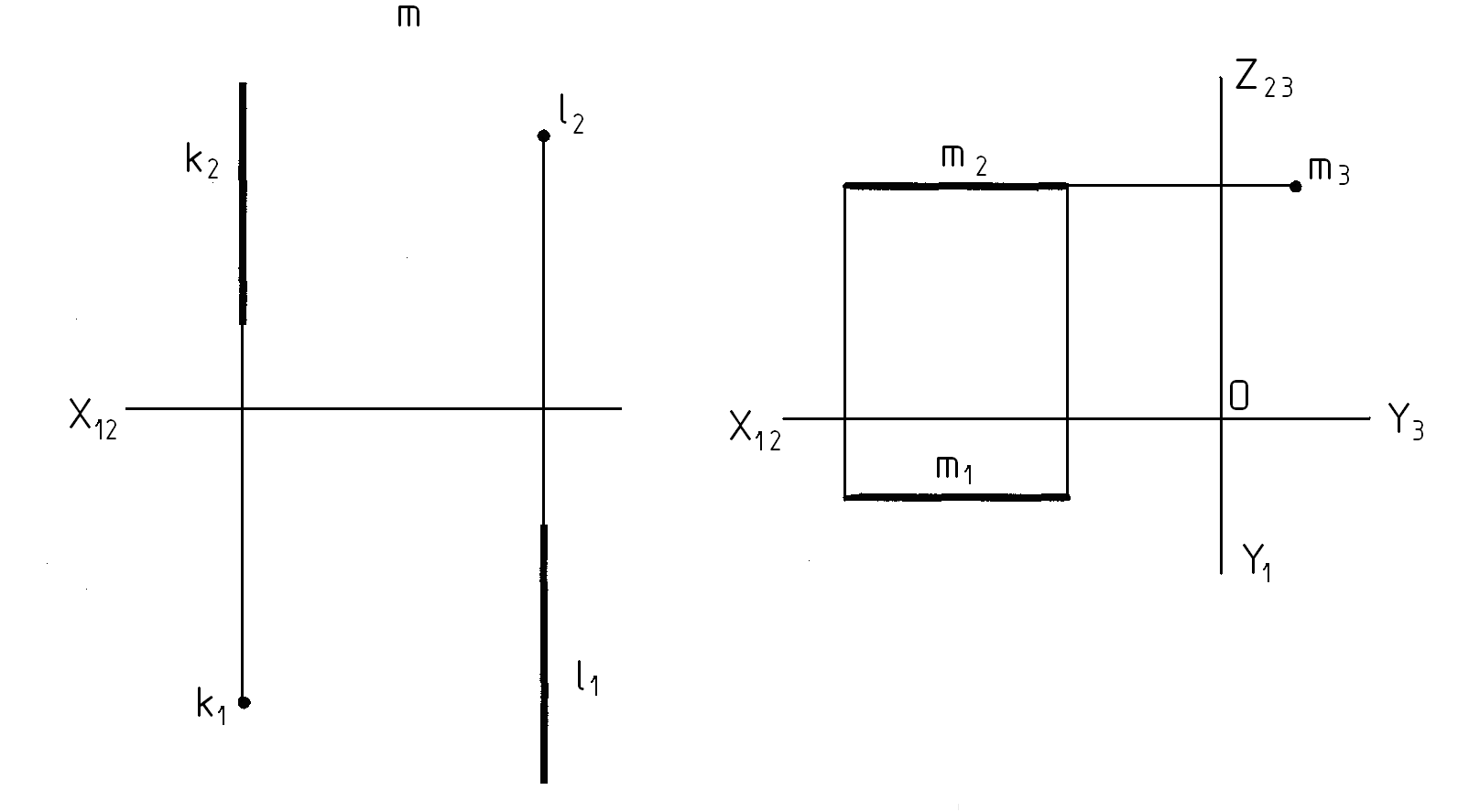
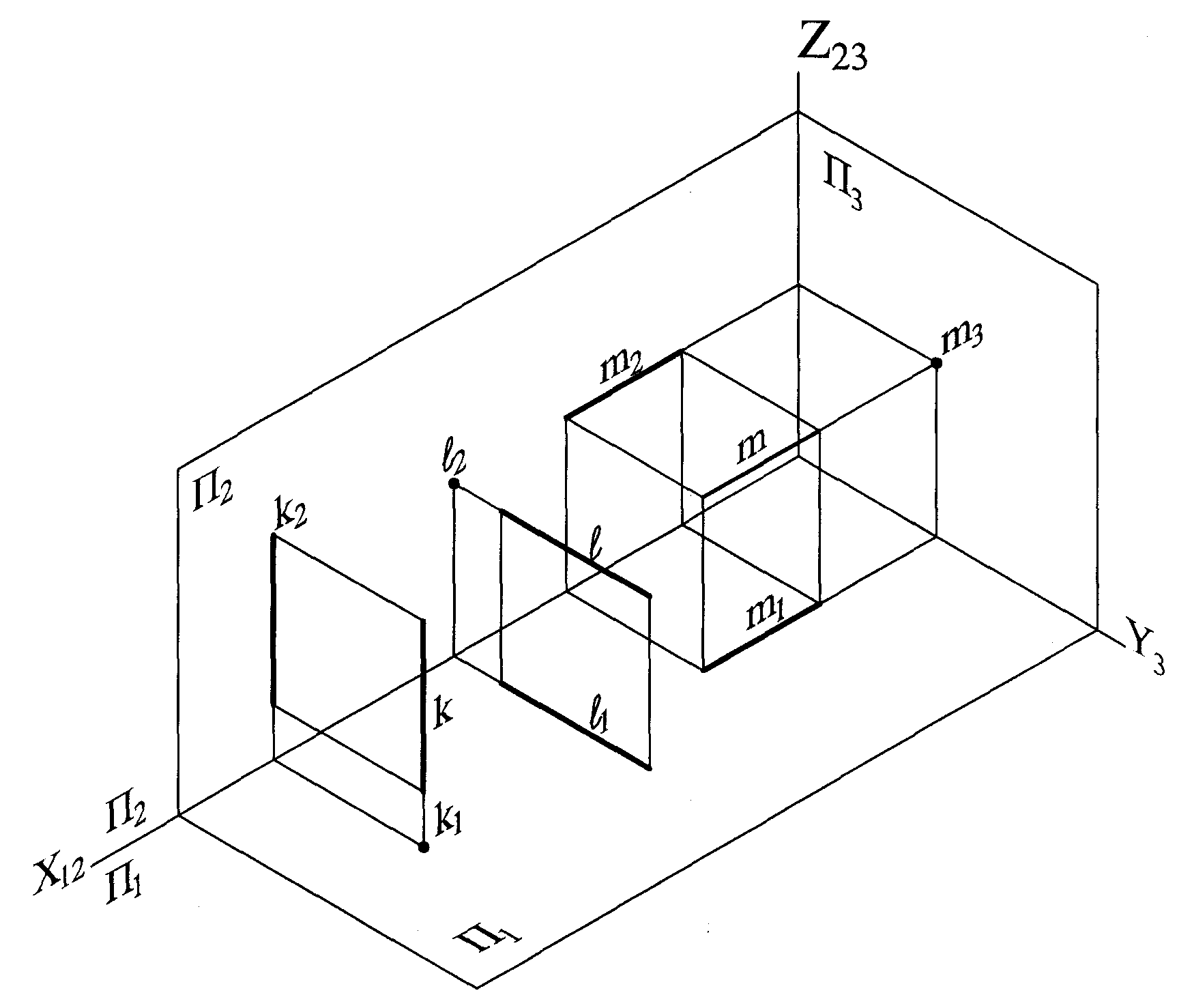
Рис. 1.47- Прямые проецирующие: а - наглядное изображение;
б - чертеж
k – горизонтально- проецирующая прямая
l – фронтально проецирующая прямая
m – профильно - проецирующая прямая
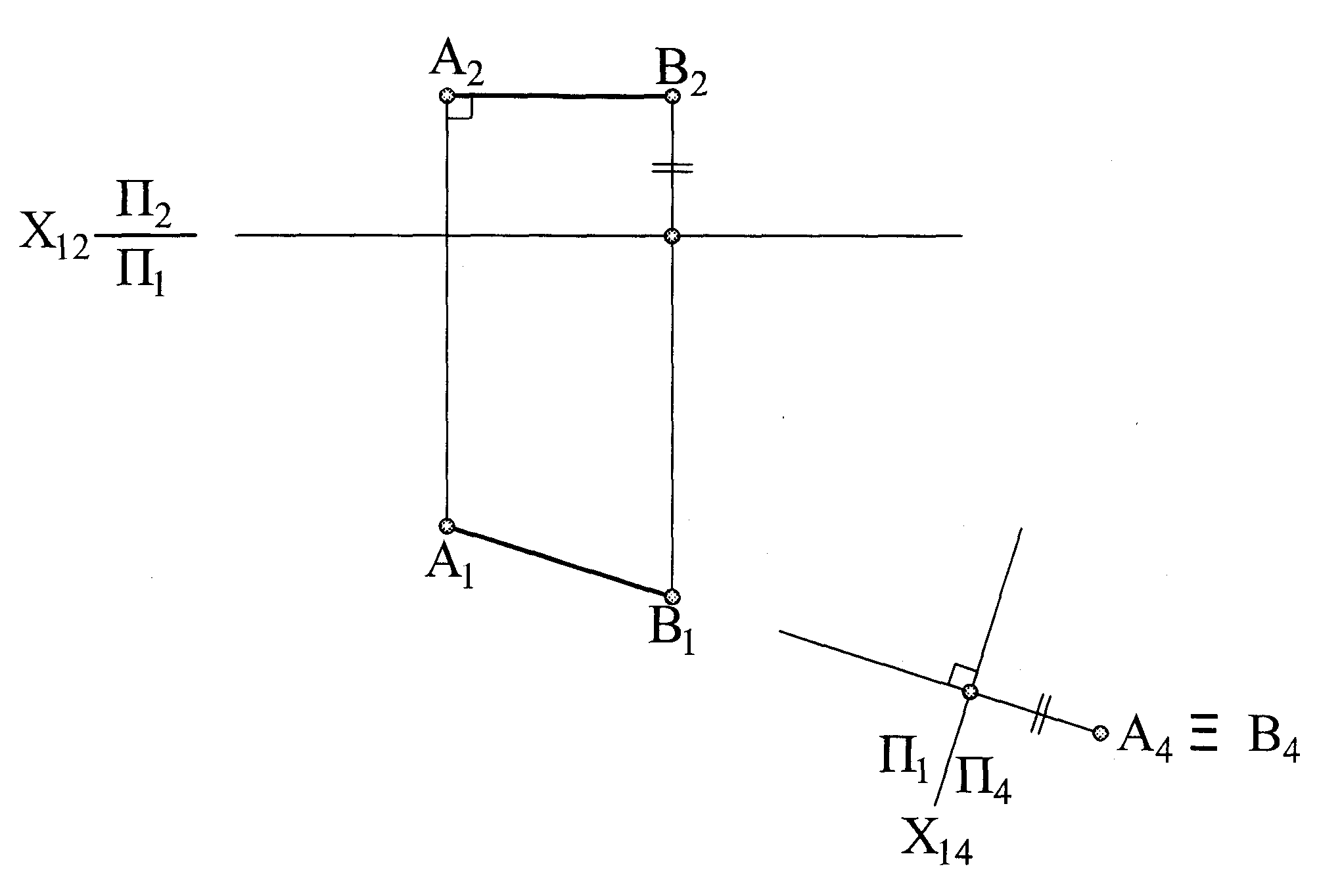
Рис. 1.48 – Преобразование отрезка горизонтального уровня в проецирующий отрезок способом замены плоскостей проекций

Рис. 1.49 – Построение истинной величины треугольника
частного положения
Задача 4. Преобразовать чертеж плоскости общего положения так, чтобы относительно новой плоскости проекций она заняла проецирующее положение.
Плоскость общего положения задана плоской фигурой (треугольник DEF). Решение следует выполнять в определенной последовательности, как показано на рис. 1.50.
В плоскости треугольника провести линию уровня h (h2, h1).
Ввести новую плоскость П4 перпендикулярно линии уровня и плоскости П1.
Спроецировать треугольник DEF на плоскость П4.
Проекция D4E4F4 представляет собой прямую линию, а это значит, что плоскость треугольника DEF заняла по отношению плоскости П4 проецирующее положение.
Угол α – угол наклона плоскости треугольника DEF к горизонтальной плоскости проекций П1. Решена еще одна метрическая задача: определение угла наклона плоскости к плоскости проекций.
Если задачу продолжить, ввести новую плоскость П5 параллельно треугольнику DEF, то можно определить его истинную величину - D5E5F5. Построение приведено на рис. 1.50.

Рис. 1.50 - Построение натуральной величины плоской
фигуры общего положения
