
- •Раздел «Преобразования плоскости»
- •Тема 6. Движения. Свойства движений
- •1. Типовые задачи с решениями
- •2. Задачи для решения на практическом занятии
- •3. Задачи для самостоятельного решения
- •Тема 7. Аналитическое выражение движений
- •1. Типовые задачи с решениями
- •2. Задачи для решения на практическом занятии
- •3. Задачи для самостоятельного решения
- •Тема 8. Приложение движений плоскости к решению задач
- •1. Типовые задачи с решениями
- •2. Задачи для решения на практическом занятии
- •3. Задачи для самостоятельного решения
- •Тема 9. Подобие плоскости. Гомотетия. Приложение гомотетии к решению задач
- •1. Типовые задачи с решениями
- •2. Задачи для решения на практическом занятии
- •3. Задачи для самостоятельного решения
- •Тема 10. Аффинные преобразования плоскости
- •Типовые задачи с решениями
- •2. Задачи для решения на практическом занятии
- •3. Задачи для самостоятельного решения
Раздел «Преобразования плоскости»
Тема 6. Движения. Свойства движений
1. Типовые задачи с решениями
Задача 1.1.
Построить образ окружности
![]() при скользящей симметрии, заданной
вектором
при скользящей симметрии, заданной
вектором
![]() и осью
и осью
![]() ,
где
,
где
![]() (рис. 6).
(рис. 6).
Р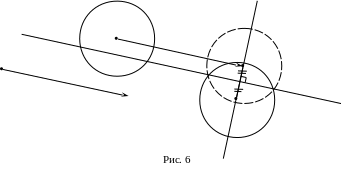 ешение.
ешение.
По определению
скользящей симметрии сначала строим
образ окружности
![]() при параллельном переносе
при параллельном переносе
![]() ,
т.е.
,
т.е.
![]() (для этого достаточно построить образ
(для этого достаточно построить образ
![]() центра
центра
![]() окружности
,
а радиус окружности
окружности
,
а радиус окружности
![]() равен
равен
![]() ).
Заметим, что окружность
строить не обязательно, достаточно
построить ее центр
).
Заметим, что окружность
строить не обязательно, достаточно
построить ее центр
![]() .
.
Затем строим образ
![]() окружности
при осевой симметрии
окружности
при осевой симметрии
![]() ,
т.е.
,
т.е.
![]() .
.
![]() ,
следовательно,
− искомая окружность.
,
следовательно,
− искомая окружность.
Задача 1.2.
На окружности
отмечены три точки
![]() и
и
![]() так, что точка
так, что точка
![]() делит пополам дугу
делит пополам дугу
![]() .
Доказать, что
.
Доказать, что
![]() .
.
Р ешение.
Так как
ешение.
Так как
![]() ,
то
,
то
![]() ,
причем дуга
,
причем дуга
![]() отобразится на дугу
отобразится на дугу
![]() (рис. 7). Тогда точка
(рис. 7). Тогда точка
![]() перейдет в такую точку
перейдет в такую точку
![]() на дуге
,
что дуги
на дуге
,
что дуги
![]() и
и
![]() будут равны. А так как по условию
будут равны. А так как по условию
![]() и
− середина
,
то точка
совпадет с
,
т.е.
и
− середина
,
то точка
совпадет с
,
т.е.
![]() .
.
Тогда по определению
осевой симметрии
![]() есть серединный перпендикуляр к отрезку
есть серединный перпендикуляр к отрезку
![]() ,
т.е.
.
,
т.е.
.
Задача 1.3. Доказать, что при центральной симметрии прямая, проходящая через центр симметрии, переходит в себя, а прямая, не проходящая через центр симметрии, переходит в параллельную ей прямую.
Р ешение.
а) Пусть
ешение.
а) Пусть
![]() −
центр симметрии и прямая
−
центр симметрии и прямая
![]() проходит через точку
(рис. 8, а).
проходит через точку
(рис. 8, а).

а)
б)
Рис. 8
Возьмем на прямой
произвольную точку
.
Пусть
![]() .
Тогда по определению центральной
симметрии
− середина отрезка
.
Тогда по определению центральной
симметрии
− середина отрезка
![]() .
Следовательно,
.
Следовательно,
![]() .
.
Так как
![]() ,
то
,
то
![]() .
Учитывая, что
,
получаем, что
.
Учитывая, что
,
получаем, что
![]() совпадает с
совпадает с
![]() ,
т.е.
,
т.е.
![]() .
.
б) Пусть
![]() (рис. 8, б). Возьмем точки
(рис. 8, б). Возьмем точки
![]() и найдем
и
и найдем
и
![]() .
Тогда
.
Тогда
![]() .
.
Диагонали
![]() и
и
![]() четырехугольника
четырехугольника
![]() пересекаются и точкой пересечения
делятся пополам. Следовательно,
− параллелограмм, откуда получаем, что
пересекаются и точкой пересечения
делятся пополам. Следовательно,
− параллелограмм, откуда получаем, что
![]() ,
т.е.
,
т.е.
![]() .
.
2. Задачи для решения на практическом занятии
2
 .1.
Параллельный перенос задается парой
соответственных точек
.1.
Параллельный перенос задается парой
соответственных точек
![]() .
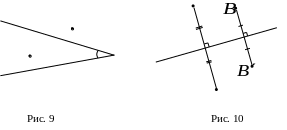
Построить образ угла (рис. 9).
.
Построить образ угла (рис. 9).
2.2. Известно,
что
![]() (рис. 10). Назовите все пары прямых,
проходящих через эти точки и симметричных
относительно
.
(рис. 10). Назовите все пары прямых,
проходящих через эти точки и симметричных
относительно
.
2
 .3.
Построить образ данной прямой
.3.
Построить образ данной прямой
![]() при осевой симметрии, заданной парой
соответственных точек
(рис. 11).
при осевой симметрии, заданной парой
соответственных точек
(рис. 11).
2 .4.
Построить образ луча
.4.
Построить образ луча
![]() при повороте вокруг точки
на угол
при повороте вокруг точки
на угол
![]() (рис. 12).
(рис. 12).
2.5.
Известно, что
![]() .
Укажите образ точки
.
Укажите образ точки
![]() ,
образ точки
,
образ точки
![]() ,
прообраз точки
(рис. 13).
,
прообраз точки
(рис. 13).
2.6.
В четырехугольнике
![]() .
Доказать, что
.
Доказать, что
![]() .
.
2.7.
Начертите два непараллельных отрезка
![]() и
и
![]() ,
длины которых равны. Построить центр
поворота, отображающего
на
(
в
,
а
− в
,
длины которых равны. Построить центр
поворота, отображающего
на
(
в
,
а
− в
![]() ).
Сколько существует таких поворотов? А
если
).
Сколько существует таких поворотов? А
если
![]() ?
?
3. Задачи для самостоятельного решения
3.1. Построить образ угла при параллельном переносе, заданном парой соответственных точек (рис. 14).

3.2.
Построить образ тупого угла
![]() при повороте вокруг точки
,
лежащей внутри угла, на угол
при повороте вокруг точки
,
лежащей внутри угла, на угол
![]() (рис. 15).
(рис. 15).
3.3.
Две окружности
![]() и
и
![]() неравных радиусов пересекаются в точках
и
.
Доказать, что точки
и
симметричны относительно прямой
неравных радиусов пересекаются в точках
и
.
Доказать, что точки
и
симметричны относительно прямой
![]() .
.
3 .4.
Известно, что
.4.
Известно, что
![]() −
образ
при повороте (рис. 16). Как построить образ
точки
−
образ
при повороте (рис. 16). Как построить образ
точки
![]() с помощью одного циркуля?
с помощью одного циркуля?
3.5.
Известно, что
![]() (рис. 17). Как с помощью одной линейки
построить точку пересечения высот
(рис. 17). Как с помощью одной линейки
построить точку пересечения высот
![]() ,
если точка
,
если точка
![]() пересечения высот
пересечения высот![]() дана?
дана?
