Показатели вариации

Вариация признака – это изменение значений признака у единиц статистической совокупности, которые обусловлены влиянием действия различных факторов.

Существует две группы показателей вариации:

1. абсолютные;

1. относительные.

Первая абсолютная величина, с помощью которой измеряется вариация признака, - размах вариации.

Размах вариации (R) – это разность между наибольшим и наименьшим значениями признака.

Определяется размах вариации следующим образом:

,

где x_max – максимальное значение признака,

x_min – минимальное значение признака.

Следовательно, величина размаха вариации зависит от крайних значений признака и не отражает колеблемости признака у основной массы единиц совокупности.

На практике нередко необходим такой показатель, который будет отражать вариацию значений признаков от их средней (общей) величины. К таким показателям относятся:

• среднее линейное отклонение;

• дисперсия;

• среднее квадратическое отклонение.

Среднее линейное отклонение отражает все колебания варьирующего признака и представляет собой среднюю арифметическую из абсолютных значений отклонений вариант от средней величины, т.к. сумма отклонений значений признака от средней равно 0, то все отклонения берутся по модулю.

Простая

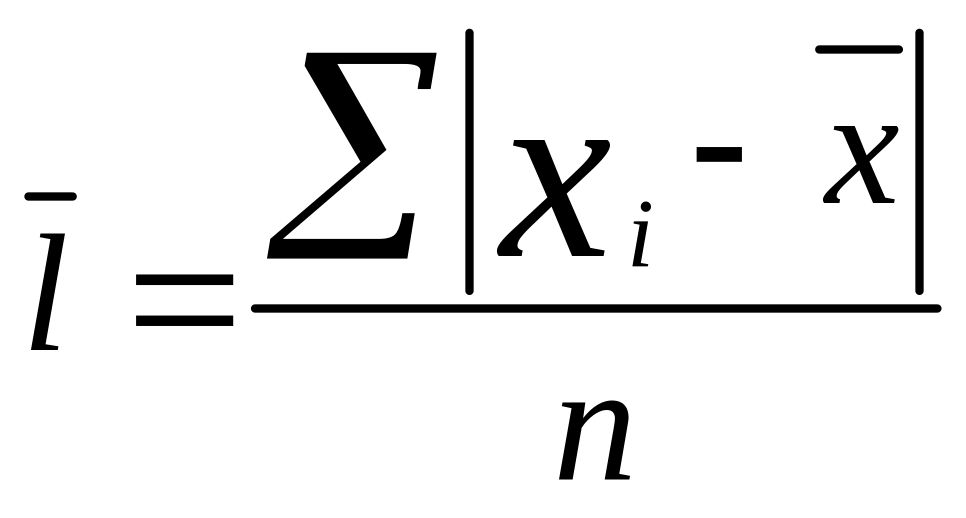
Взвешенная

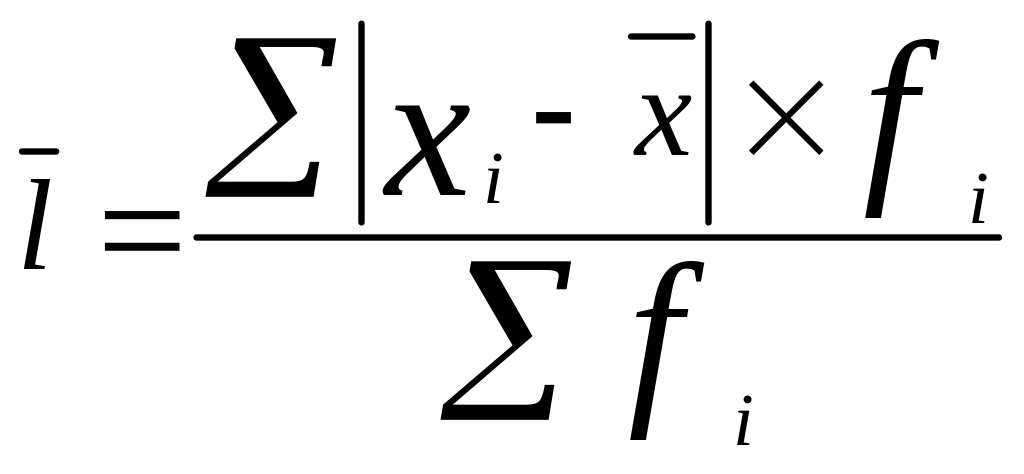
Дисперсия – средний квадрат отклонений значений признака от их средней величины.

Невзвешенная формула:

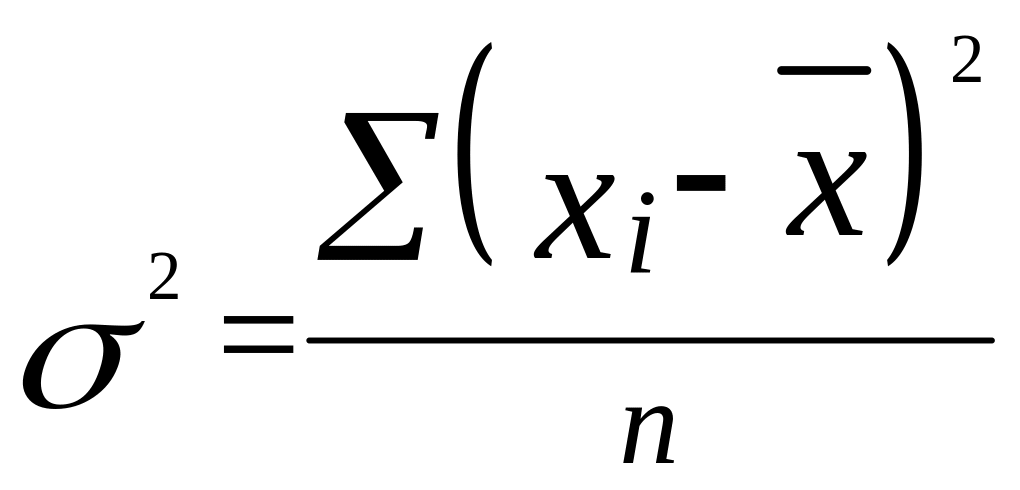
Взвешенная формула:

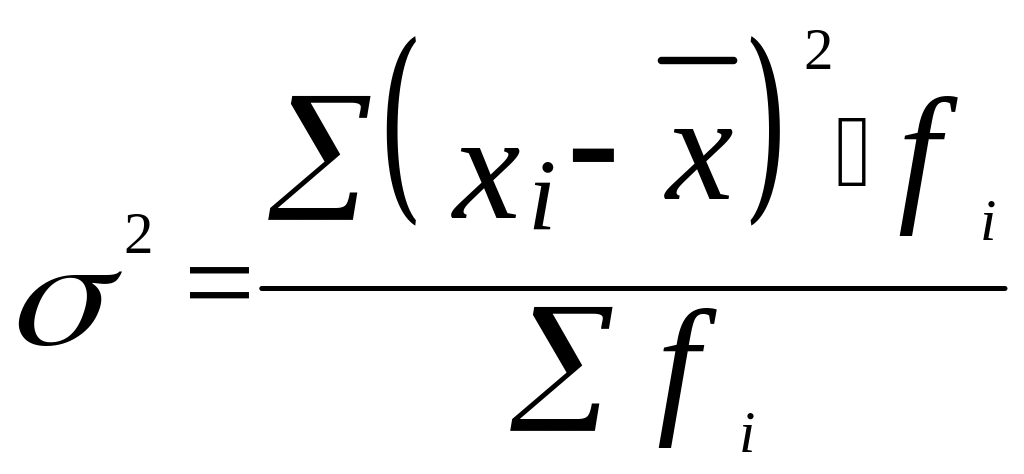
Наиболее удобным и широко распространенным на практике показателем является среднее квадратическое отклонение. Оно определяется как квадратный корень из дисперсии и имеет ту же размерность, что и изучаемый признак.

Невзвешенная формула:

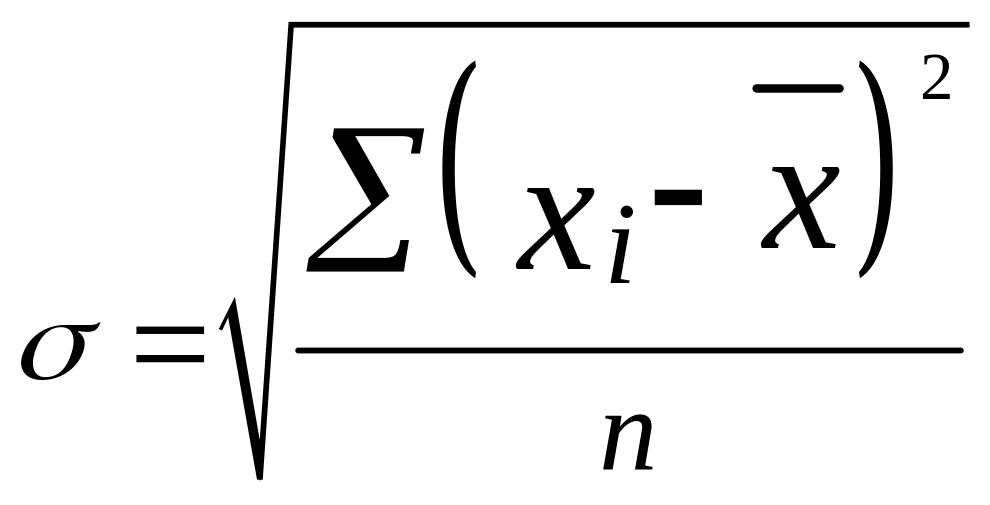
Взвешенная формула:

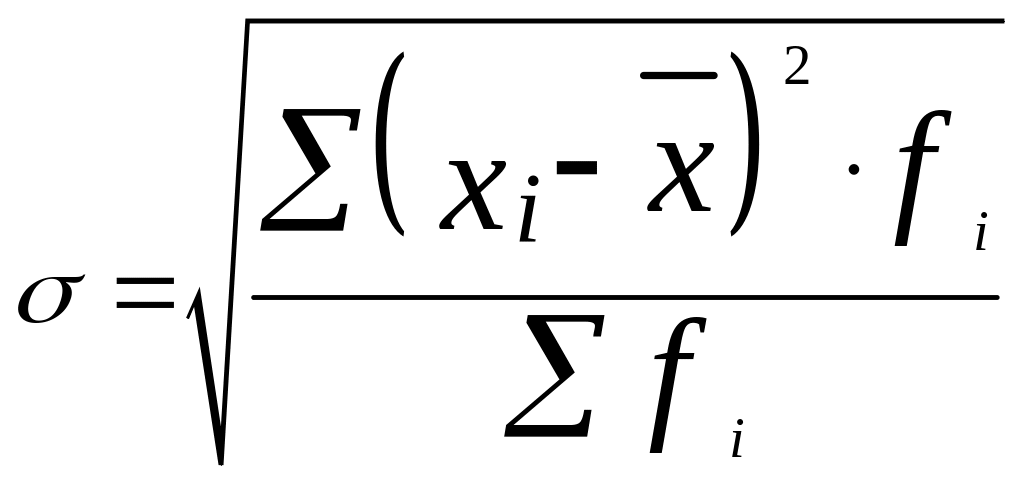
Рассмотренные показатели позволяют получить абсолютное значение вариации, т.е. оценивают ее в единицах измерения исследуемой совокупности. В отличие от них, коэффициент вариации измеряет колеблемость в относительном выражении, относительно среднего уровня, что во многих случаях является предпочтительнее:

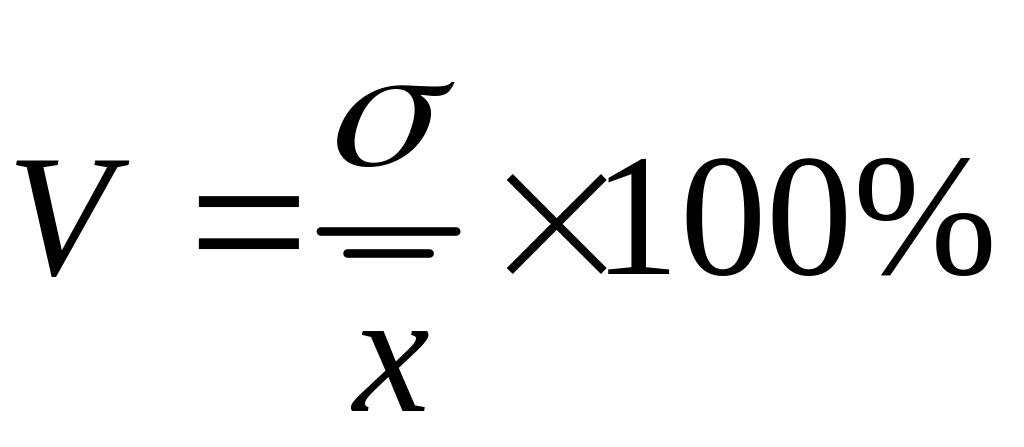
Если коэффициент вариации не превышает 33%, то совокупность по рассматриваемому признаку можно считать однородной.

Примеры решения задач

Задача 1.

План товарооборота по каждой из трёх секций магазина был установлен в сумме 20 тыс. руб.

Таблица 11

Секция	Выполнение плана товарооборота, %
1	102
2	97
3	101

Вычислите средний процент выполнения плана по магазину.

Решение:

Так как план товарооборота для каждой из секций установлен в одном и том же размере для решения задачи возможно применить формулу средней арифметической простой:

Ответ: средний процент выполнения плана по магазину 100%.

Задача 2. Остатки товаров на складе на 1 число месяца составили, тыс. руб.:

Таблица 12

Месяц	январь	февраль	март	апрель
Остатки	11 200	14 602	15 600	13 400

Определите среднемесячные остатки товаров на складе за 1 квартал

Решение:

Решение задачи проведем по формуле средней хронологической, которая имеет следующий вид:

Применим эту формулу для решения нашей задачи:

y= (11200/2+14602+15600+13400/2)/ (4-1)

y= (5600+14602+15600+6700)/3

y= 14167, 3

Ответ: среднемесячные остатки товаров на складе составляют 14167,3 тыс. руб.

Задача 3. По двум магазинам имеются данные о распределении работников по уровню заработной платы за сентябрь:

Таблица 13

Месячная заработная плата, руб.	Число работников
1000-1200	30
1200-1400	38
1400-1600	140
1600-1800	75
1800-2000	35

Определить: моду средней заработной платы.

Решение:

1. Определим модальный интервал. Им будет являться интервал 1400-1600 руб.

1. Определим моду по формуле:

;

Ответ: Мода средней заработной платы равна 1522 рубля.

Задача 4. Имеются следующие данные по расположению магазинов от базы снабжения (км.)

Таблица 14

Магазин	Расположение магазина от базы снабжения, км. (x)
1	2
2	3
3	4
4	6
5	10

Определить медиану расположения магазинов от базы снабжения.

Решение:

Представим решение в табличной форме:

Таблица 15