Задания для самостоятельного выполнения

Задача 1. Рассчитайте абсолютный прирост, темп роста, темп прироста средних товарных запасов базисным и цепным методом. Расчеты оформите в таблице. Сделайте вывод.

Таблица 27

Товарные запасы предприятия за ряд лет

Года	2005	2006	2007	2008	2009	2010	2011
Товарные запасы, тыс. руб.	27,8	28,2	29	31,4	33,6	34,8	33,9

Задача 2. На основании приведённых данных определите: абсолютный прирост товарооборота, темпы роста и темпы прироста (цепным и базисным способом).

Таблица 28

Квартал	Товарооборот, (тыс. руб.)
І	15,6
ІІ	18,2
ІІІ	17,3
ІV	19,0

Сделайте выводы по результатам расчётов.

Контрольные вопросы:

1. Что такое статистический ряд распределения?

1. Как можно классифицировать ряды распределения?

2. Что такое варианта и частота?

3. Что такое ряд динамики?

4. Как можно классифицировать ряды динамики?

5. Какие показатели характеризуют изменение уровней ряда динамики? Как их можно рассчитать?

6. Как проводится анализ сезонных колебаний товарооборота?

Глава 6. Статистические индексы

Индекс (лат. index) – это относительная величина, показывающая, во сколько раз уровень изучаемого явления в данных условиях отличается от уровня того же явления в других условиях.

Различие условий может проявляться во времени, в пространстве и в выборе в качестве базы сравнения какого-либо условного уровня.

По охвату элементов совокупности различают индексы индивидуальные и сводные, которые делятся на общие и групповые.

Индивидуальные индексы – это результат сравнения двух показателей, относящихся к одному объекту.

В статистико-экономическом анализе деятельности предприятий и отраслей широко применяются индивидуальные индексы качественных и количественных показателей.

Индивидуальный индекс цены определяется по формуле:

Индекс цен характеризует относительное изменение уровня цены единицы каждого вида продукции, в отчётном периоде по сравнению с базисным, и является качественным показателем.

Индекс физического объема определяется по формуле:

Сводный индекс характеризует соотношение уровней нескольких элементов совокупности. Если изучаемая совокупность состоит из нескольких групп, то сводные индексы, каждый из которых характеризует изменение уровней отдельной группы единиц, являются групповыми (субиндексами), а сводный индекс, охватывающий всю совокупность единиц, - общим (тотальным) индексом.

Сводные индексы выражают соотношение сложных социально-экономических явлений и состоят из двух частей:

1. из индексируемой величины;

2. из соизмерителя, который называется вес.

Показатель, изменение которого характеризует индекс, называется индексируемым. Индексируемые показатели могут быть двоякого рода. Один из них измеряют общий, суммарный размер (объем) того или иного явления и условно называются объемными, экстенсивными. Эти показатели получаются как итог непосредственного подсчёта или суммирования и являются исходными, первичными.

Другие показатели измеряют уровень явления или признака в расчёте на ту или иную единицу совокупности и условно называются качественными, интенсивными: выработка продукции в единицу времени (или на одного работника); затраты рабочего времени на единицу продукции и т.д.

Эти показатели получаются путем деления объемных показателей, т.е. носят расчётный, вторичный характер.

Они измеряют интенсивность, эффективность явления или процесса и, как правило, являются либо средними, либо относительными величинами.

При использовании индексного метода применяется определённая символика, т.е. система условных обозначений.

Каждый индексируемый показатель обозначается определённой буквой (обычно латинской).

Индивидуальные индексы являются обычными относительными величинами, т.е. могут быть названы индексами только в широком понимании этого термина.

Индексы в узком смысле, или собственно индексы, - это тоже показатели относительные, но особого рода. Они имеют более сложную методику построения и расчёта, а специфические приемы их построения и составляют суть индексного метода.

Социально-экономические явления и характеризующие их показатели могут быть соизмеримыми. Так, объемы продукции или товаров одного и того же вида и сорта, произведенных на разных предприятиях или проданных в разных магазинах, соизмеримы и могут суммироваться, а объемы разных видов продукции или товаров несоизмеримы и непосредственно суммироваться не могут.

Первая особенность индексного метода и собственно индексов состоит в том, что индексируемый показатель рассматривается во взаимосвязи с другими показателями.

Умножая индексируемый показатель на другой, связанный с ним, мы сводим различные явления к их единству, обеспечиваем их количественную сравнимость и учитываем их вес в реальном экономическом процессе. Поэтому показатели – сомножители, связанные с индексируемыми показателями, принято называть весами индексов, а умножение на них – взвешиванием.

Агрегатные индексы.

Агрегатный индекс – сложный показатель, который характеризует среднее изменение социально-экономического явления, состоящего из несоизмеримых элементов. Особенность этой формы индекса состоит в том, что непосредственно сравниваются две суммы одноименных показателей.

При выборе веса индекса следует руководствоваться правилом: если строится индекс количественного показателя, то веса берутся за базисный период, при построении индекса качественного показателя используются веса отчетного периода.

Индекс стоимости продукции (товарооборота) ( ) - представляет собой отношение стоимости продукции текущего периода к стоимости продукции в базисном периоде. Стоимость продукции – это произведение количества продукции в натуральном выражении (q) на цену (p).

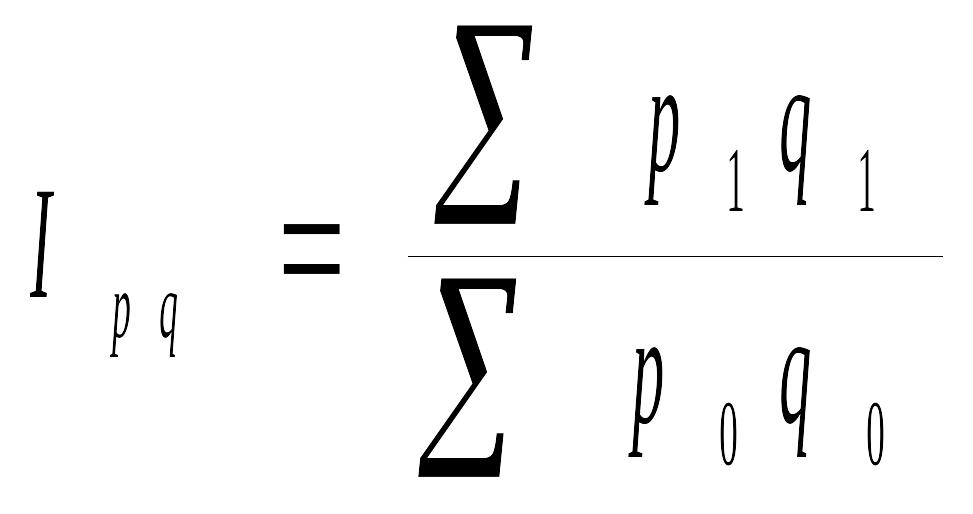
Показывает, во сколько раз возросла (уменьшилась) стоимость продукции отчетного периода по сравнению с базисным, или сколько процентов составляет.

Индекс физического объема продукции – это индекс количественного показателя. Индексируемой величиной будет количество продукции, а весом – цена.

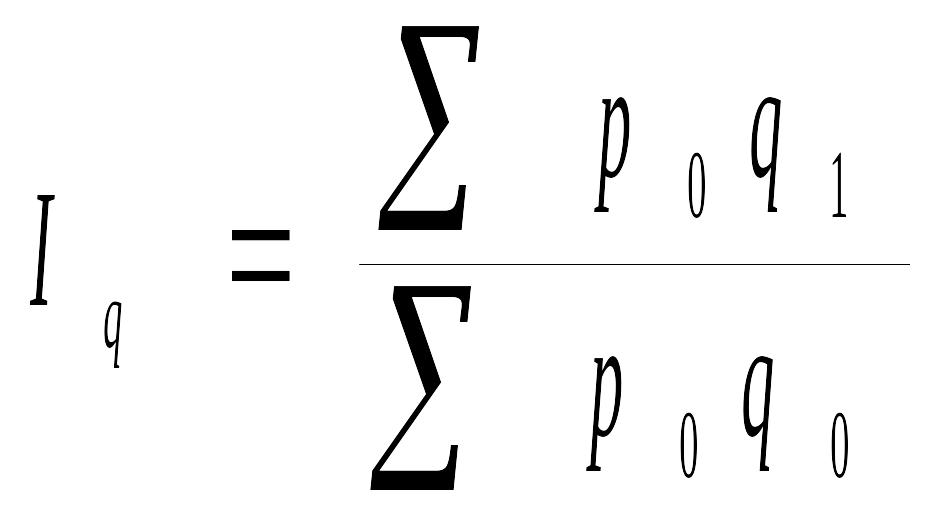
показывает, во сколько раз возросла (уменьшилась) стоимость продукции из-за изменения объемов ее производства.

Разность числителя и знаменателя ( ) показывает, на сколько рублей изменилась стоимость продукции в результате изменения объема.

Индекс цен – это индекс качественного показателя. Индексируемой величиной будет цена товара, т.к. этот индекс характеризует изменение цен. Весом будет выступать количество произведенного товаров.

,

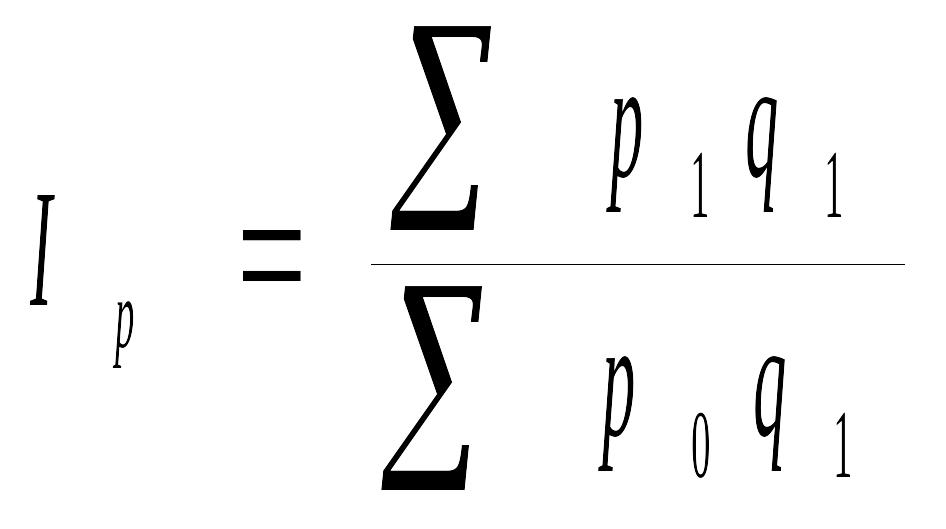в числителе – фактическая стоимость продукции текущего периода, а в знаменателе – условная стоимость тех же товаров ценах базисного периода. Показывает, во сколько раз возросла (уменьшилась) стоимость продукции из-за изменения цен. Разность числителя и знаменателя – на сколько рублей изменилась стоимость продукции в результате роста (снижения) цен.

Стоимость продукции можно представить как произведение количества товара на его цену. Точно такая же связь существует и между индексами стоимости, физического объема и цен, т.е. , или

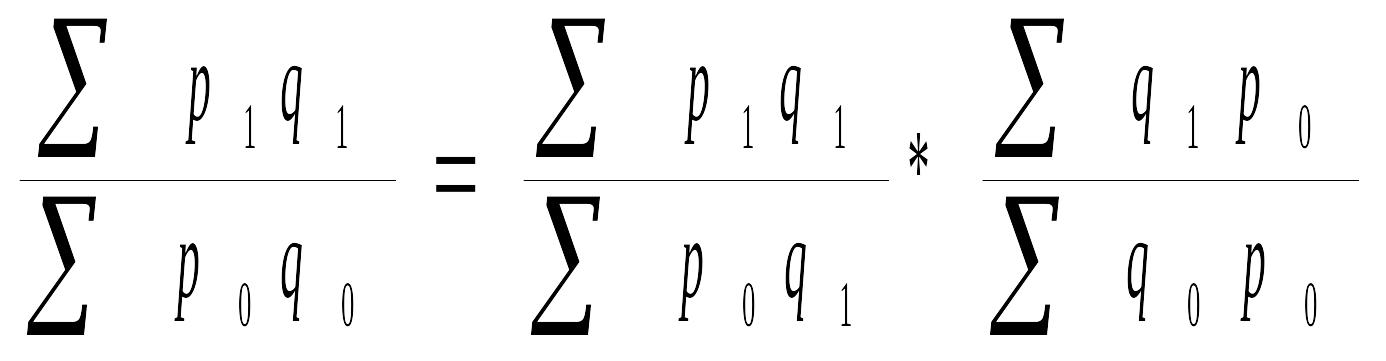
Разность числителя и знаменателя каждого индекса-сомножителя выражает размер изменения общей абсолютной величины под влиянием изменения одного фактора.

Примеры решения задач:

Задача 1.

Имеются следующие данные о поставке продовольственных товаров с оптовых предприятий в розничную торговлю за два года:

Таблица 29

Товарные группы	Базисный год		Отчётный год
	Тонны	Цена за 1 кг, руб.	Выручка от реализации, тыс. руб.	Цена за 1 кг, руб.
Макаронные изделия	50	13,0	937,2	14,2
Кондитерские изделия	67	10,0	960	12,0
Сахар	112	14,0	1815	16,5
Мука	230	13,0	3300	15,5

Вычислить:

1. Индивидуальный индекс цен.

1. Индивидуальный индекс физического объема.

2. Общие индексы цен, товарооборота и физического объема продукции в целом по магазину.

Решение:

1. Вычислим индивидуальный индекс цен.

Для этого применим формулу индивидуального индекса цены:

Индивидуальный индекс цены (макаронные изделия): 109,2% ((14,2 / 13) ×100)

Индивидуальный индекс цены (кондитерские изделия): 120,0% ((12 / 10)× 100)

Индивидуальный индекс цены (сахар): 117,9% ((16,5/14) ×100)

Индивидуальный индекс цены (мука): 119,2% ((15,5/13) × 100)

1. Вычислим индивидуальный индекс физического объема:

а) Рассчитаем физический объем (тонны) в отчётном году, для чего выручку от реализации в отчётном году разделим на цену в отчётном году:

Макаронные изделия - 66

Кондитерские изделия - 80

Сахар - 110

Мука – 213

б) Для расчёта индивидуального индекса физического объема применим формулу расчёта такого индекса:

Индивидуальный индекс физического объёма (макаронные изделия): 132,0% ((66 / 50) ×100)

Индивидуальный индекс физического объема (кондитерские изделия): 119,0% ((80 / 67)× 100)

Индивидуальный индекс физического объема (сахар): 102,0% ((110/112) ×100)

Индивидуальный индекс физического объема (мука): 93% ((213,0/230) × 100)

2. Рассчитаем общие индексы цены и товарооборота:

Применим формулы:

Индекс стоимости продукции (товарооборота):

Индекс физического объема продукции

Индекс цены:

Получим следующие результаты:

1. Индекс стоимости продукции (товарооборота) в целом по магазину равен

I_pq =

2. Индекс физического объема продукции в целом по магазину равен:

I_q =

3. Индекс цены в целом по магазину равен:

I_p =

Задача 2.

Товарооборот в базисном периоде составил 27 млн. руб., в отчетном периоде в фактических ценах – 32 млн. руб., а в ценах базисного периода – 30 млн. руб. Вычислите общий индекс цен.

Решение:

Для решения задачи применим формулу:

Ответ: Общий индекс цены равен 106,67%

Задача 3.

Определите общий индекс физического объёма на основании данных: товарооборот отчётного периода составил 80 тыс. руб., а товарооборот базисного периода – 65 тыс. руб. Общий индекс цен за этот период составил 1,02.

Решение:

1. Рассчитаем общий индекс товарооборота по формуле:

1. Рассчитаем общий индекс физического объема продажи, используя формулу взаимосвязи индексов:

Из этой формулы получим, что индекс физического объема равен:

Задача 4. На основании данных таблицы вычислите общий индекс цен.

Таблица 30

Товар	Товарооборот (тыс. руб.)		Изменение цены, в %
	Базисный период	Отчётный период
А	102	120	- 2
Б	91	80	+ 3
В	137	120	+ 4

Решение:

1. Рассчитайте индивидуальные индексы цен, используя данные об изменении цены по каждой группе товаров:

Определим индивидуальные индексы цен по каждой группе товаров:

i_p (А) = (100 + (- 2) / 100 = 0,98

i_p (Б) = (100 + (+3) / 100 = 1,03

i_p (В) = (100+ (+4) / 100 = 1,04

1. Рассчитайте общий индекс цен по формуле средней гармонической:

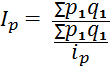
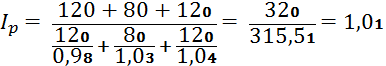
Ответ: Общий индекс цен равен 1,01 или 101%

Задача 5.

Как изменится товарооборот, если цены вырастут на 2%, а количество проданного товара на 1%?

Решение:

1. Рассчитайте общий индекс цен по формуле:

1. Рассчитайте общий индекс физического объёма продажи товаров:

2. Рассчитайте общий индекс товарооборота из формулы взаимосвязи индексов:

Применим формулы для решения данной задачи:

1. 

1. 

2. 

Ответ: товарооборот увеличится на 3%

Задача 6.

На основании данных таблицы вычислите общий индекс физического объема товарооборота.

Таблица 31

Товар	Товарооборот базисного периода (тыс. руб.)	Изменение количества товаров
А	25	+3
Б	43	+8
В	36	+2

Решение:

1. Рассчитайте индивидуальные индексы физического объема продажи с учётом изменения количества продажи по каждой группе:

1. Рассчитайте общий индекс физического объема продажи по формуле средней арифметической:

Применим формулы:

1. Рассчитаем индивидуальные индексы физического объема:

1. Рассчитаем общий индекс физического объема продажи:

=

Ответ: общий индекс физического объема товарооборота равен 1,05 или 105%.

Задания для самостоятельного выполнения:

Задача 1.

Известны следующие данные по продовольственному магазину:

Таблица 32

Товары	Количество реализованных товаров в периоде, кг.		Цена 1 кг. (руб.) в периоде
	базисном	текущем	базисном	текущем
Масло	2000	2100	240	250
Сыр	650	750	265	280

Вычислите индивидуальные и общие индексы цен, физического объема товарооборота и стоимости реализованных товаров. Какую формулу следует применить при вычислении первых двух индексов?

Задача 2.

Ниже приведены данные о товарообороте двух сравниваемых периодов (в ценах соответствующих лет) и индексах физического объема товарооборота:

Таблица 33

Товары	Фактический товарооборот (тыс. руб.) в периоде		Индексы физического объема товарооборота, %
	базисном	текущем
Овощи	105,4	107,6	105,0
Мясо и мясные изделия	896,2	902,3	110,6

Вычислите общие индексы в следующей последовательности: физического объема товарооборота, стоимости реализованных товаров и цен.

Задача 3.

Вычислите на сколько процентов изменился товарооборот в фактических ценах, если индекс цен составил 1,3, а индекс товарооборота в сопоставимых ценах 1,02.

Пояснение. Выполнить решение задачи, используя формулу взаимосвязи индексов.

Задача 4. Рассчитайте общий индекс физического объема по данным: товарооборот отчётного периода в фактических ценах составил 50 тыс. руб., а в базисных – 45 тыс.руб. Товарооборот базисного периода составил 48 тыс. руб.

Задача 5. Товарооборот базисного периода – 120 тыс. руб., отчётного периода – 150 тыс. руб. Общий индекс физического объема товарооборота 1,38. Определите общий индекс цен.

Контрольные вопросы:

1. Что такое индекс?

1. Что такое индивидуальные индексы и как они рассчитываются?

2. Что характеризует сводный индекс и из каких частей состоит?

3. Что такое агрегатные индексы?

4. Приведите виды агрегатных индексов и формулы их расчёта.

5. Приведите формулу взаимосвязи индексов товарооборота, физического объёма и цен.

ЗАКЛЮЧЕНИЕ

БИБЛИОГРАФИЧЕСКИЙ СПИСОК