
- •Ю. В. Краснолуцкая статистика
- •Введение
- •Глава 1. Статистическое наблюдение
- •Примеры решения задач
- •Данные о распределении населения Минусинского района по полу
- •Задания для самостоятельного выполнения
- •Глава 2. Сводка и группировка Методические указания
- •Примеры решения задач
- •Распределение сотрудников предприятия по уровню доходов
- •Исходные данные
- •Вспомогательная таблица
- •Зависимость товарооборота от торговой площади магазина
- •Исходные данные
- •Глава 3. Абсолютные и относительные величины
- •Данные для расчётов
- •Глава 4 средние величины и показатели вариации
- •Структурные средние
- •Показатели вариации
- •Определение медианы расположения магазинов от базы снабжения (км.)
- •Задания для самостоятельного выполнения
- •Данные о продаже мужских костюмов
- •Глава 5. Ряды динамики и ряды распределения
- •5.1. Методические указания
- •Ряды динамики
- •Показатели, характеризующие изменение уровней ряда динамики во времени
- •Анализ сезонных колебаний товарооборота
- •Примеры решения задач
- •Средние товарные запасы предприятия за ряд лет
- •Темпы роста средних товарных запасов, рассчитанные цепным методом
- •Темпы роста средних товарных запасов, рассчитанные базисным методом
- •Задания для самостоятельного выполнения
- •Глава 6. Статистические индексы
Анализ сезонных колебаний товарооборота
Многие ряды динамики подвержены сезонным колебаниям. Периодичность подъема или спада присуща не только природным явлениям, но и человеческой деятельности (экономическая активность населения, инвестирование физическими лицами в кредитных организациях, покупательная способность среднедушевых денежных доходов населения, уровень сезонных продаж товаров и т.д.).
Сезонные колебания – это такие изменения, которые соответствуют строго периодическому ритму в определённой причинной связи за длительный временной интервал.
Существуют различные способы расчёта индекса сезонности, которые зависят от наличия или отсутствия основной тенденции.
Рассмотрим индекс сезонности, который рассчитывается как отношение среднего уровня соответствующего месяца к общей средней:
где yi - средний уровень показателя по одноимённым месяцам за ряд лет (средний уровень соответствующего месяца);
y – общий уровень показателя (общая средняя).
Примеры решения задач
Задача 1. Рассчитайте темп роста средних товарных запасов цепным методом. Расчеты оформите в таблице. Сделайте вывод.
Таблица 21
Средние товарные запасы предприятия за ряд лет
-
Года
2005
2006
2007
2008
2009
2010
2011
Товарные запасы, тыс. руб.
27,8
28,2
29
31,4
33,6
34,8
33,9
Решение:
Для решения задачи применим формулу расчёта темпа роста цепным методом.
Формула:
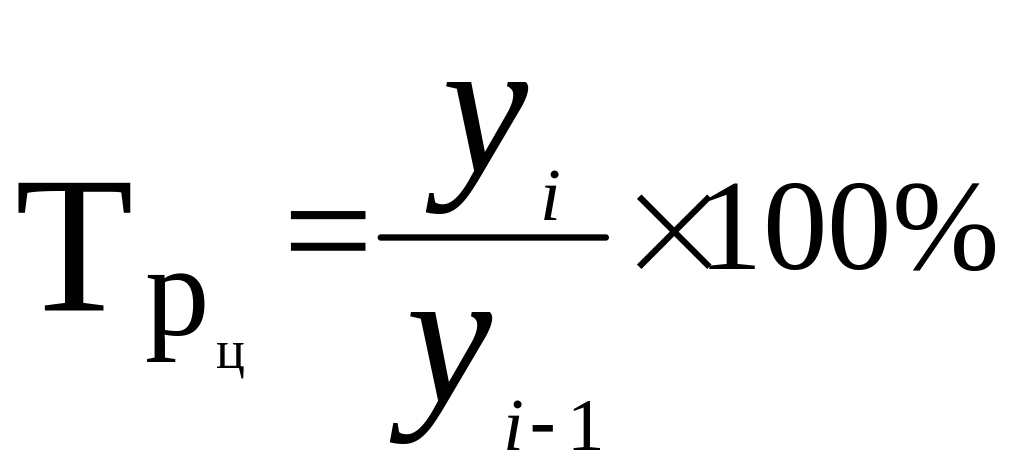
Решение задачи оформим в таблице.
Таблица 22
Темпы роста средних товарных запасов, рассчитанные цепным методом
Год |
Темп роста и его расчёт |
2005 |
- |
2006 |
101,44 ((28,2/27,8)×100%) |
2007 |
102,84 ((29/28,2) ×100%) |
2008 |
108,28 ((31,4/29)×100%) |
2009 |
107,01 ((33,6/31,4)×100%) |
2010 |
103,57 ((34,8/33,6)×100%) |
2011 |
97,41 ((33,9/34,8)×100%) |
Вывод: Анализируя темпы роста средних товарных запасов, мы можем отметить, что на протяжении 5 лет они возрастали, а в последнем году наметилась тенденция их снижения.
Задача 2. Рассчитайте темп роста товарных запасов базисным методом.
Сделайте вывод.
Таблица 23
-
Года
2005
2006
2007
2008
2009
2010
2011
Товарные запасы, тыс. руб.
27,8
28,2
29
31,4
33,6
34,8
33,9
Решение:
Для решения задачи воспользуемся формулой расчёта темпа роста базисным методом.
Формула:
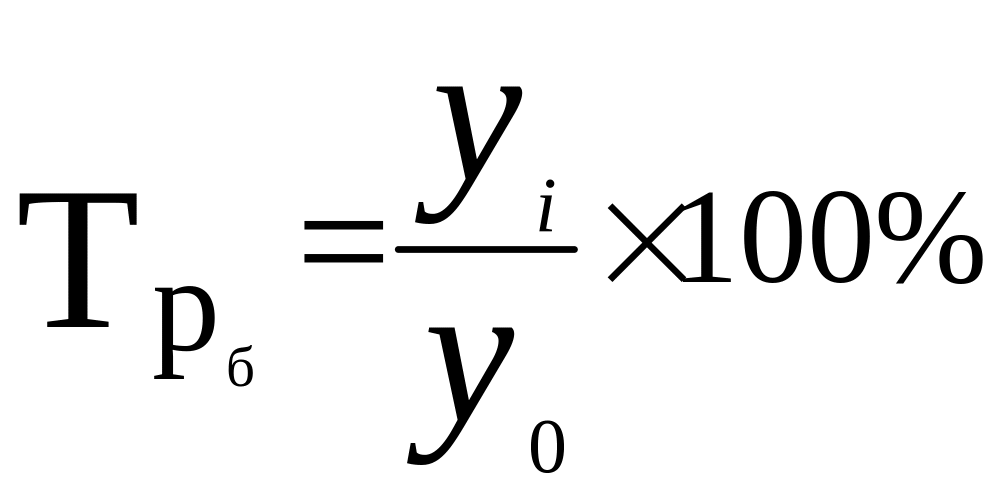
Решение задачи оформим в таблице.
Таблица 24
Темпы роста средних товарных запасов, рассчитанные базисным методом
Года |
Темп роста и его расчёт |
2005 |
- |
2006 |
(28,2:27,8)×100 = 101,44 |
2007 |
(29:27,8)×100 = 104,32 |
2008 |
(31,4:27,8)×100 = 112,95 |
2009 |
(33,6:27,8)×100 = 120,86 |
2010 |
(34,8:27,8)×100 = 125,18 |
2011 |
(33,9:27,8)×100 = 121,94 |
Вывод: Проанализировав данные таблицы можно сделать вывод, что темпы роста на протяжении всех лет возрастали по сравнению с базисным периодом. Оценить положительное это явление или нет, можно только определив, с чем было связано (в каждом году), увеличение товарных запасов.
Задача 3.
Имеем следующие данные об объеме продаж мороженого в городе (таблица)
Таблица 25
Месяц |
Год |
||
2009 |
2010 |
2011 |
|
Январь |
57,8 |
132,9 |
93,7 |
Февраль |
101,2 |
148,3 |
144,6 |
Март |
125,7 |
175,3 |
168,5 |
Апрель |
147,4 |
187,7 |
317,3 |
Май |
389,3 |
593,6 |
485,8 |
Июнь |
373,5 |
694,2 |
591,9 |
Июль |
481,9 |
489,5 |
573,2 |
Август |
197,8 |
378,4 |
295,7 |
Сентябрь |
159,0 |
254,8 |
192,6 |
Октябрь |
98,9 |
177,6 |
151,8 |
Ноябрь |
53,8 |
95,2 |
117,3 |
Декабрь |
86,1 |
102,0 |
105,4 |
Определить: индексы сезонности.
Решение:
Для анализа внутригрупповой динамики определим индексы сезонности.
Средний уровень объема продаж мороженого за каждый месяц получим делением суммы соответствующего уровня на число лет, т.е.:
![]() =94,8
=94,8
![]() ;
;
![]() и т.д.
и т.д.
Общая средняя получается делением суммы уровней объема продаж мороженого за все три года на общее число месяцев, т.е. 36:
![]()
Индексы сезонности для каждого месяца будут следующими:
Jсез(январь)
= ![]()
Jсез
(февраль) = ![]()
Jсез
(март) = ![]() и т.д.
и т.д.
Результаты расчётов представлены в таблице:
Таблица 26
Результаты расчёта индексов сезонности
Месяц |
Год |
Индекс сезонности, % |
|||
2009 |
2010 |
2011 |
В среднем за три года |
||
Январь |
57,8 |
132,9 |
93,7 |
94,8 |
38,2 |
Февраль |
101,2 |
148,3 |
144,6 |
131,4 |
52,9 |
Март |
125,7 |
175,3 |
168,5 |
156,5 |
63,0 |
Апрель |
147,4 |
187,7 |
317,3 |
217,5 |
87,6 |
Май |
389,3 |
593,6 |
485,8 |
489,6 |
197,2 |
Июнь |
373,5 |
694,2 |
591,9 |
553,2 |
222,8 |
Июль |
481,9 |
489,5 |
573,2 |
514,9 |
207,4 |
Август |
197,8 |
378,4 |
295,7 |
290,6 |
117,0 |
Сентябрь |
159,0 |
254,8 |
192,6 |
202,1 |
81,4 |
Октябрь |
98,9 |
177,6 |
151,8 |
142,8 |
57,5 |
Ноябрь |
53,8 |
95,2 |
117,3 |
88,8 |
35,8 |
Декабрь |
86,1 |
102,0 |
105,4 |
97,8 |
39,4 |
Итого |
2272,4 |
3429,5 |
3237,8 |
- |
- |
