Остовное дерево минимальной стоимости
Остовным деревом графа G называется свободное дерево, содержащее все вершины графа G.
Зададим цену дуг. Стоимость остовного дерева равна сумме цен дуг его образующих. Тогда для исходного графа G можно построить несколько вариантов остовных деревьев с различной стоимостью а на практике имеет место нахождение такого подмножества дуг остовного дерева, для которого суммарная стоимость будет минимальна (максимальна).
Алгоритм Прима. Алгоритм Крускала.
Эти алгоритмы основаны на основном свойстве ОДМС.
Пусть G=V,e связный граф с заданной функцией стоимости на множестве рёбер. Обозначим через U подмножество вершин V.
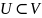
Если u,v – ребро для которого u∈ U, a v∈(V\U)
Наименьшее по цене из всех рёбер вида (u,v), то это ребро является ребром ОДМС.
Алгоритм Прима
Каждый шаг в алгоритме Прима добавляет в множество U очередной узел.
Шаг 1. Инициализируем множество U некоторым узлом в лексикографическом порядке.
Шаг 2. Для каждого узла из множества U перебираем инцидентные им дуги с целью найти минимальную дугу вида (u,v) где u∈U; v∈(V\U).
Шаг 3. Для найденной дуги другой инцидентный ей узел добавляем в U.
Шаг 4. Шаги 2 и 3 повторяем до тех пор, пока множество U не станет равное V.
Исходный граф – связный.
procedure (var A:array[1..n,1..n] of Integer; C:array[1..n] of real)
var i,j,k,imin,jmin:integer; s,min:real; bfound:boolean;
begin
for i:=1 to n do mark[i]:=false;
mark[1]:=true;
for k:=1 to n-1 do for i:=1 to n do if mark[i] then
begin
bfound:=false;
for j:=1 to n do
if (A[i,j]=1) and (not mark[j]) and (((C[i,j]<min) and bfound) or not bfound)
begin
min:=C[i,j]; imin:=i; jmin:=j;
end;
mark[jmin]:=true; s:=s+min;
end;
end;
Алгоритм Крускала
Алгоритм Крускала предполагает, что множество U уже содержит все вершины. Тогда задача нахождения ОДМС состоит в том, чтобы выбрать самые минимальные допустимые дуги, не образующие цикла, так как дерево – ациклический граф. Поэтому алгоритм Крускала состоит из следующих шагов:
Упорядочить (отсортировать) дуги в порядке возрастания их цены.
Перебирая упорядоченную последовательность дуг, добавлять в ОДМС дугу, не образующую цикл.
Согласно свойству свободных деревьев, таких дуг ровно n-1 штук.
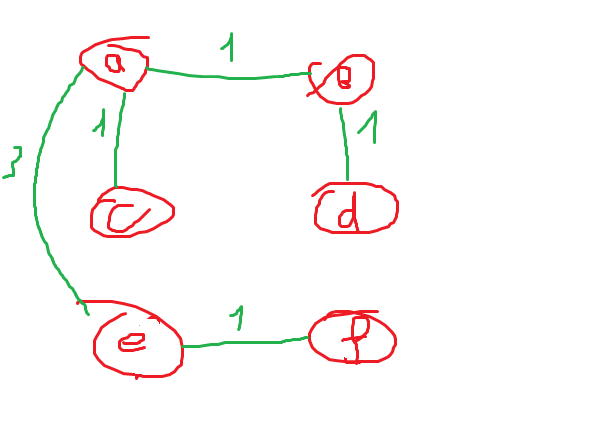
Трудоёмкость Крускала. O(N^5)
Паросочетания и покрытия графов.
Подмножество рёбер
графа
,
такие что никакие два ребра из этого
подмножества не инцидентны какой-либо
вершине из V называется
паросочетанием.
Практическое применение находит задача о нахождении максимального паросочетания – такого допустимого паросочетания, при котором число задействованных в паросочетании дуг максимально. Часто максимальное паросочетание ищется при помощи построения чередующейся (аугментальной).
Полное паросочетание – задействованы все вершины графа.
В данной задаче ищутся отношения между узлами или объектами предметной области; другая задача состоит в выборе такого подмножества дуг, которые бы задействовало бы все вершины графа. Это называется покрытием.
Покрытием графа называется множество вершин, инцидентных хотя бы одной дуге. С практической точки зрения это означает, что необходимо задействовать каждый объект при этом наименее избыточным способом.
Например, найти такое разбиение дисциплин между преподавателями, чтобы у дисциплины был строго один преподаватель, но преподаватель может читать несколько дисциплин, при этом каждый преподаватель должен участвовать в учебном процессе (поэтому и у дисциплин может быть в худшем случае несколько преподавателей).
В этом случае решается задача о минимальном покрытии – нахождении такого минимально возможного подмножества дуг, чтобы каждая вершина в графе G имела бы хотя бы одну инцидентную ей дугу из этого подмножества.
Существует алгоритм перехода от задачи нахождения минимального покрытия к задаче максимального паросочетания и наоборот.
Пусть С – допустимое максимальное паросочетание графа G. Найдём вершину, не инцидентную ни одной дуге.
Выберем для такой вершины допустимую инцидентную ей дугу графа G и добавим дугу к списку дуг, который был инициализирован паросочетанием. Если несвязных вершин не найдено, то тогда полученный список дуг образует минимальное покрытие и наоборот: если из минимального покрытия удалять дуги, образующие инцидентным им вершинам степень больше 1, то в итоге получаем максимальное допустимое паросочетание.