
- •6. ##1.4.19.1(4) Найти обратную матрицу для данной .
- •9. ##2.8.25.1(2) При каких значениях и прямые и параллельны
- •10. ##1.5.32.2(1) Определить, имеет ли система решение, если да, то решить систему уравнений по формулам Крамера
- •12. ##2.4.52.2(1) Уравнение определяет
- •2. ##1.2.14.1(5) Дано: . Найти определитель матрицы а.
- •5. ##2.5.22.1(3) Расстояние от точки до плоскости вычисляется по формуле
- •6. ##1.4.13.1(1) Найти обратную матрицу для данной .
- •10. ##1.5.33.2(4) Определить, имеет ли система решение, если да, то решить систему уравнений по формулам Крамера
- •12. ##2.4.56.2(4) Уравнение определяет
- •6. ##1.4.14.1(2) Найти обратную матрицу для данной .
- •10. ##1.5.34.2(2) Определить, имеет ли система решение, если да, то решить систему уравнений по формулам Крамера
- •12. ##2.4.55.2(5) Уравнение определяет
- •2. ##1.2.14.1(5) Дано: . Найти определитель матрицы а.
- •5. ##2.5.22.1(3) Расстояние от точки до плоскости вычисляется по формуле
- •6. ##1.4.18.1(4) Найти обратную матрицу для данной .
- •10. ##1.5.35.2(1) Определить, имеет ли система решение, если да, то решить систему уравнений по формулам Крамера
- •12. ##2.4.48.2(4) Уравнение определяет
2. ##1.2.14.1(5) Дано: . Найти определитель матрицы а.
Ответы: 1 ). 2 ). 3 ). 4 ). 5 ).
3. ##1.6.8.1(2) Закончить утверждение. Вектор, начало и конец которого совпадают, называется ...
Ответы: 1 ). противоположным 2 ). нулевом 3 ). единичным 4 ). все предложенные ответы неверны 5 ). сонаправленным
4.
##2.1.11.1(3) Угол между
двумя прямыми
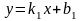 и
и
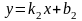 вычисляется по формуле
вычисляется по формуле
Ответы:
1 ).  2 ).
2 ). 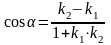 3 ).
3 ).  4 ).
4 ).  5 ).
5 ). 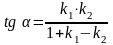
5. ##2.5.22.1(3) Расстояние от точки до плоскости вычисляется по формуле
Ответы: 1 ). 2 ). 3 ). 4 ). 5 ).
6. ##1.4.18.1(4) Найти обратную матрицу для данной .
Ответы:
1 ).  2 ).
2 ).  3 ).
3 ). 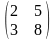 4 ).
4 ). 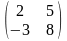 5 ). нет правильного ответа
5 ). нет правильного ответа
7.
##2.2.13.1(2) Найти угловой
коэффициент прямой, проходящей через
точки
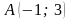 и
и

Ответы:
1 ). 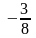 2 ).
3 ).
2 ).
3 ). 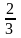 4 ).
4 ). 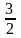 5 ).
5 ). 
8.
##2.6.8.1(3) Найти длину
перпендикуляра, опущенного из точки
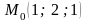 на плоскость
на плоскость

Ответы:
1 ). 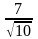 2 ).
3 ).
2 ).
3 ). 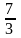 4 ).
5 ).
4 ).
5 ). 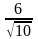
9.
##2.8.1.1(5) Написать
уравнения прямой, проходящей через
точки
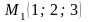 и
и
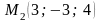
Ответы:
1 ). 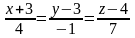 2 ).
2 ).  3 ).
3 ).  4 ).
4 ).  5 ).
5 ). 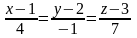
10. ##1.5.35.2(1) Определить, имеет ли система решение, если да, то решить систему уравнений по формулам Крамера
Ответы:
1 ). 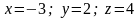 2 ). система уравнений несовместна
3 ). бесчисленное множество
решений 4 ).
2 ). система уравнений несовместна
3 ). бесчисленное множество
решений 4 ).  5 ).
5 ). 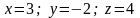
11.
##1.8.51.2(3) Дан треугольник
с вершинами
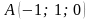 ,
,
 ,
,
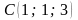 .
Вычислить его площадь.
.
Вычислить его площадь.
Ответы:
1 ). нет
правильного ответа
2 ).
3 ). 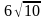 4 ).
5 ).
4 ).
5 ). 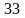
12. ##2.4.48.2(4) Уравнение определяет
Ответы: 1 ). эллипс 2 ). окружность 3 ). гиперболу 4 ). две пересекающиеся прямые 5 ). параболу
13.
##2.10.23.2(1) Вычислить
расстояние
от точки
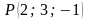 до прямой
до прямой
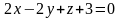 ,
,
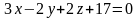
Ответы:
1 ). 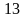 2 ).
2 ). 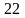 3 ).
3 ). 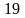 4 ).
4 ).  5 ).
5 ). 
14.
##2.4.175.3(5) Кривая,
определяемая уравнением
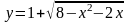 ,
изображена на рисунке
,
изображена на рисунке
Ответы: 1 ). 2 ). 3 ). 4 ). 5 ).
15.
##2.12.21.3(3) Поверхность,
определяемая уравнением
 ,
изображена на рисунке
,
изображена на рисунке
Ответы: 1 ). 2 ). 3 ). 4 ). 5 ).
