Задания для контрольной работы

Каждый студент должен решить 8 задач своего варианта. Номер варианта совпадает с последней цифрой учебного номера (шифра) студента. Например, для варианта №6 следует решить задачи №№ 6, 16, 26, 36, 46, 56, 66, 76; для варианта №0 следует решить задачи №№ 10, 20, 30, 40, 50, 60, 70, 80.

1–10. Даны вершины треугольника АВС.

Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС и их угловые коэффициенты; 3) угол А в радианах; 4) уравнение высоты СD и ее длину; 5) уравнение окружности, для которой высота СD есть диаметр; 6) систему линейных неравенств, определяющих треугольник АВС.

1. А (–5; 0), В (7; 9), C (5; –5).

2. A (–7; 2), B (5; 11), С (3; –3).

3. А (–5; –3), В (7; 6), C (5; –8).

4. А (–6; –2), В (6; 7), C (4; –7).

5. А ( –8; –4), В (4; 5), C (2; –9).

6. А (0; –1), В (12; 8), С (10; –6).

7. А (–6; 1), В (6; 10), С (4; –4).

8. А (–2; –4), В (10; 5), С (8; –9).

9. А (–3; 0), В (9; 9), С (7; –5).

10. А (–9; –2), В (3; 7), С (1; –7).

11–20. Решить данную систему уравнений с помощью формул Крамера. Сделать проверку полученного решения.

11. 12.

13. 14.

15. 16.

17. 18.

19. 20.

21–30. Систему уравнений записать в матричной форме и решить ее с помощью обратной матрицы. Сделать проверку полученного решения.

21. 22.

23. 24.

25. 26.

27. 28.

29. 30.

31-40. Исследовать функцию y = f(x) и построить ее график. Найти наибольшее и наименьшее значения функции y = f(x) на отрезке [a, b].

31. a =  1 , b = 3

32. a =  1 , b = 2

33. a = 2 , b = 3

34. a =  1 , b = 2

35. a = 0 , b = 4

36. a=  2 , b= 3

37. a =  3 , b = 0

38. a = 3 , b = 1

39. a = 1 , b = 4

40. a =  1 , b = 4

4150. Найти с помощью определенного интеграла площадь плоской фигуры, расположенной в первой четверти и ограниченной заданными параболой, прямой и осью Ох.

41.

42.

43.

44.

45.

46.

47.

48.

49.

50.

51–60. В ящике содержится n одинаковых, тщательно перемешанных шаров, причем k из них – красные, l – синие и m – белые. Наудачу вынимается один шар. Найти вероятность того, что вынутый шар а) синий, б) белый, в) цветной.

  51. n = 8, k = 3, l = 3, m = 2.

  52. n = 9, k = 4, l = 1, m = 4.

  53. n = 10, k = 3, l = 5, m = 2.

  54. n = 11, k = 5, l = 3, m = 3.

  55. n = 12, k = 4, l = 6, m = 2.

  56. n = 8, k = 1, l = 5, m = 2.

  57. n = 9, k = 3, l = 4, m = 2.

  58. n = 10, k = 2, l = 7, m = 1.

  59. n = 11, k = 2, l = 4, m = 5.

60. n = 12, k = 3, l = 5, m = 4.

61–70. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение дискретной случайной величины Х, заданной законом распределения.

₆1. 

xi	1	3	5	7
pi	0,2	0,1	0,4	0,3

₆₂. 

xi	2	4	6	8
pi	0,5	0,1	0,3	0,1

₆₃. 

xi	2	3	5	7
pi	0,1	0,2	0,3	0,4

₆₄. 

xi	1	2	3	4
pi	0,6	0,1	0,1	0,2

₆₅. 

xi	10	12	15	20
pi	0,3	0,2	0,1	0,4

₆₆. 

xi	5	10	15	20
pi	0,1	0,3	0,1	0,5

₆₇. 

xi	10	15	20	25
pi	0,1	0,2	0,4	0,3

₆₈. 

xi	2	4	6	8
pi	0,2	0,1	0,4	0,3

₆₉. 

xi	2	4	5	6
pi	0,6	0,2	0,1	0,1

₇₀. 

xi	3	4	6	7
pi	0,3	0,2	0,4	0,1

71–80. Известны математическое ожидание a и среднеквадратическое отклонение  нормально распределенной случайной величины X. Написать плотность вероятности и найти вероятность попадания этой величины в заданный интервал (; ).

71. a = 11,  = 5,  = 5,    = 10.

72. a = 10,  = 4,  = 6,    = 11.

73. a = 9,  = 1,  = 7,    = 12.

74. a = 8,  = 2,  = 4,    = 10.

75. a = 7,  = 3,  = 4,    = 12.

76. a = 6,  = 5,  = 4,    = 8.

77. a = 5,  = 2,  = 2,    = 7.

78. a = 4,  = 3,  = 1,    = 9.

79. a = 3,  = 2,  = 3,    = 8.

80. a = 2,  = 1,  = 1,    = 4.

Примечание: для контрольной работы следует взять тетрадь в клеточку; представлять рукописный вариант; условия задач переписывать; на титульном листе необходимо указать (можно в напечатанном виде) следующее: МГИИТ, контрольная работа по математике студента ФИО заочного обучения (4,5 года), курс, группа, шифр (по зачётной книжке), номер варианта. Проверил: ФИО преподавателя.

Методические указания к решению задач

Примеры решения и оформления заданий приведены в учебно-методических пособиях [8] , [9].

Элементы линейной алгебры, аналитической геометрии и линейного программирования.

По теме «Аналитическая геометрия» рассмотрим решение типовой задачи.

Задача 1.Даны вершины треугольника АВС: А(-4;8), В(5;-4), С(10;6).

Найти:

1. длину стороны АВ;

2. уравнения сторон АВ и АС и их угловые коэффициенты;

3. угол А в радианах;

4. уравнение высоты СD и ее длину;

5. уравнение окружности, для которой высота СD есть диаметр;

6. систему линейных неравенств, определяющих треугольник АВС.

Решение.

1. Найдем длину стороны АВ.

Расстояние d между точками М₁(х₁; у₁) и М₂(х₂; у₂) определяется по формуле:

(1)

Подставив в эту формулу координаты точек А и В, имеем:

АВ= .

2. Уравнение прямой, проходящей через точки М₁(х₁; у₁) и М₂(х₂; у₂), имеет вид:

(2)

Подставив в (2) координаты точек А и В, получим уравнение прямой АВ:

3у–24 =–4х –16, 4х+3у–8=0 (АВ)

Для нахождения углового коэффициента к_АВ прямой АВ, разрешим полученное уравнение относительно у: у = .

Отсюда к_АВ = .

Подставив в формулу (2) координаты точек А и С, найдем уравнение прямой АС:

х+7у–52=0 (АС).

Отсюда к_АС = .

3. Угол между двумя прямыми, угловые коэффициенты которых равны к₁ и к₂, определяется по формуле:

(3)

Угол А, образованный прямыми АВ и АС, найдем по формуле (3), подставив в нее к₁ = к_АВ = , к₁ = к_АС = .

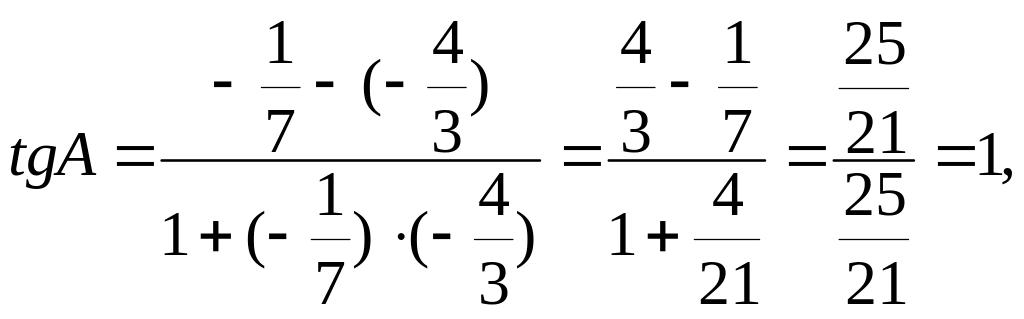
4. Так как высота СD перпендикулярна стороне АВ, то угловые коэффициенты этих прямых обратны по величине и противоположны по знаку, т.е.

к_СD = .

Уравнение прямой, проходящей через данную точку М₁(х₁; у₁) в заданном направлении, имеет вид:

(4)

Подставив в (4) координаты точки С(10;6) и к_СD = , получим уравнение высоты СD:

у – 6 = (х – 10), 4у – 24 = 3х – 30, 3х – 4у – 6 = 0 (СD). (5)

Для нахождения длины СD определим координаты точки D, решив систему уравнений (АВ) и (CD):

, откуда х = 2, у = 0, то есть D (2; 0)

Подставив в формулу (1) координаты точек С и D, находим:

СD = .

5. Уравнение окружности радиуса R с центром в точка Е( ) имеет вид:

(6)

Так как СD является диаметром искомой окружности, то ее центр Е есть середина отрезка СD. Воспользуемся формулами деления отрезка пополам, получим:

Следовательно, Е(6; 3) и R= = 5. Используя формулу (6), получаем уравнение искомой окружности:

6. Множество точек треугольника АВС есть пересечение трех полуплоскостей, первая из которых ограничена прямой АВ и содержит точку С, вторая ограничена прямой ВС и содержит точку А, а третья ограничена прямой АС и содержит точку В.

Для получения неравенства, определяющего полуплоскость, ограниченную прямой АВ и содержащую точку С, подставим в уравнение прямой АВ координаты точки С:

> 0

Поэтому искомое неравенство имеет вид: 4х+3у .

Для составления неравенства, определяющего полуплоскость, ограниченную прямой ВС и содержащую точку А, найдем уравнение прямой ВС, подставив в формулу (2) координаты точек В и С:

(ВС).

Подставив в последнее уравнение координаты точки А, имеем:

< 0. Искомое неравенство будет 2х – у – 14 . Подобным образом составим неравенство, определяющее полуплоскость, ограниченную прямой АС и содержащую точку В: < 0. Третье искомое неравенство будет х+7у –52 . Итак, множество точек треугольника АВС определяется системой неравенств:

На рис. 1 в декартовой прямоугольной системе координат хОу изображен треугольник АВС, высота СD, окружность с центром в точке Е и диаметром CD

Рис. 1