Билет 1 №4

Шарик с q = 0,2 мкКл и В = 0,1 Тл имеет L = 30 см

Решение:

F = qBυ∙ІsinαІ

ІsinαІ = cosβ F = qBυ∙cosβ

(m∙υ²)/2=mgh где g = 10 м/с²

Найдем максимальную F для этого

найдём

cos²β - 2∙sin²β = 0 cos²β – 2 + 2∙cos²β = 0 cos²β = 2/3

Билет 2 №4 Найдите внутреннюю энергию воздуха S = 1 м² , h = 8,31 км

Решение:

Дж

Билет 3 №4 Распределение заряда по пространству имеет осевую симметрию и описывается соотношением, где r – расстояние до оси симметрии

Решение:

1. Заряд заключён внутри цилиндра радиуса r и высотой l

2) Поток Ф_Д через боковую поверхность Ф_Д = = ε₀∙E∙2π∙r∙l

3) По теореме Гауса →

(Если подставить начальные данные можно построить схематично график E от r, он будет иметь вид)

Билет 3 №3 Короткий сплошной цилиндр массой m=80кг и R; лежит на горизонт. поверхности,

к основанию цилиндра прикреплена пружина с k = 0.2*10⁵ Н/м. Сместили на х₀=2 см,

t =0 , отпустили.

Найти

1. ускорение цилиндра при t = 0

2. x = x (t) F_тр

F

x

₁

Билет 4 №4 При адиабатном расширении идеального газа его объём изменился от V₁ до V₂ = 4 V₁ , а давление при этом уменьшается от P₁ до P₂ = P₁ / 8 Найти работу газа при расширении

Решение:

1. Найдём коэффициент Пуассона

2. Работа расширения

Подставим γ

Билет 5 №4 Сплошной вал m = 16 кг в виде цилиндра закреплён на горизонтальной оси,

к нему подвешено ведёрко m₀ = 2 кг из него вытекает жидкость со скоростью μ = 0,22 кг/с. Найти скорость ведёрка через t = 5 с

Решение:

1) 2-й закон Ньютона m₂q – T = m₂a где q = 10м/с²

2) Закон динамики вращательного движения для вала

→ TR = J∙ε где J = mR²/2 – момент инерции для вала

ε = a/R – угловое ускорение → T = ma/2

3) m₂q = T + m₂a → m₂q = (m₂ + m / 2)∙a →

подставим m₂ = m₀  μ∙t тогда a(t) =

3. υ ==

=

Подставив числа получим υ = 7,6 м/с

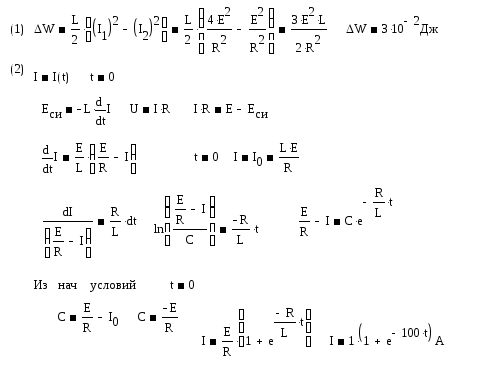
Билет 5 №3 Катушка индуктивности или соленоид с L = 20 мГн соединена в схеме с

E = 20В; R = 2 Ом

Найти :

1. на какую величину изменится W после размыкания ключа при I₂

2. I = I (t) после размыкания

Решение:

Билет 6 №4 Пузырик газа всплывает со дна водоёма h = 10 м V₁ = 5 мм³. Какую работу совершит газ при всплытии ?

Решение:

Давление в пузыре P = P₀ + gρ(h – x)

PV = P₁V₁ V = P₁V₁/P

dV =

dA = PdV → A =

A = A = 6.9 ∙10^-4 Дж

Билет 6 №3 Для измерения больших сопротивлений применяют схему с зарядом конденсатора.

Для этого измеряемый резистор подкл. последоват. с конденсатором к источнику E и через время t измеряют заряд, и рассчитывают R.

При E = 100 В и t = 1мин на кондер С = 20 мкФ натекло q = 1мКл.

Найти:

1. кол-во теплоты Q - ?

2. R - ?

Работа источника ЭДС

Билет 7 №4 Мыльная плёнка толщиной d₀ = 1.2 мкМ (n = 4/3 ) имеет форму параболы …

Решение:

1) Условие ослабления света при отражении от плёнки

или

max: (sinα = 0)

при подстановке чисел получаем k₁ = 5

min: (sinα = 1)

при подстановке чисел получаем k₂ = 4

Выразим sinα : sin²α = tgα =

→ → → k = 4 ; 5 .

Билет 7 №3 Последовательно два кондера включены с резистором R = 0.2 МОм и незамкн. ключом. Один конд. С₁ = 20 мкФ заряжен до U₀ = 200 В , на другом С₂ = 10 мкФ ноль. Ключ замкнули.

Найти :

1. Uc на обоих кондерах после прекращения тока в цепи

2. Uc2 = Uc2 (t) - ?

Билет 8 №4 Труба сечением S = 10 см²…

Решение:

1) При смещении столба жидкости на x ∆h = 2x давление столба ρg∆h = ρg2x Давление воздуха

P = P₀+ 2ρgx dV = Sdx

2) dA = PdV A =Sh₁(P₀+3ρgh₁) A = 750 дж

Работа совершается расширяющимся воздухом при увеличении V в 2 раза

Билет 8 №3 Сплошной диск m = 0.4 кг, R = 0.04 м вращается с ω₀ = 10π c^-1 . R = 0.5 Ом

В момент t₀ = 0 включается поле B = 0,2 Тл.

Найти ω = ω(t).

Р

r₀

R

ешение

1. находим ток в радиальном направлении. На элементе dr ЭДС индукции

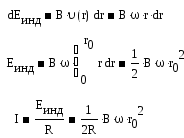
2. Сила Ампера, действующая на dr

3.

Билет 9 №4 По длинной прямой полосе 2b = 20 см течёт ток I = 10 A Найти индукцию поля B в т.А

расстояние до которой а.

1. Полоса толщиной dy вызывает в т.А магнитное поле с индукцией dB

где dI = (I/2b)∙dy x = a

интеграл домножен на 2 в виду того, что выше рассматривалась только верхняя часть полоски, а нижняя не учитывалась. μ₀ = 4π∙10^-7 Гн/м

Билет 9 №3 Два шарика r₁ = 4 см и r₂ = 2 см, нагретые до T₀ = 1000К, находятся в вакууме на расстоянии d₀ = 0.6 м. Между шарами помещена небольшая пластинка ( r₀ << d₀ ).

Найти на каком расстоянии α от первого шарика надо поместить пластину, чтобы температура ее была бы наименьшей.

Решение

r₀

r₁

r₂

d₀

1. Энергия, поглощаемая площадкой за 1с от обоих шаров.

2. Излучаемая площадкой энергия

3. При тепловом равновесии

4. находим минимум функции

Билет 10 №3 Внутри длинного теплопроводящего цилиндра, герметично закрытого с обеих сторон, находится поршень m = 10 г , l₀ = 1 м , S = 2 см² , p₀ = 100 кПа , x₀ = 2 мм. Процесс изотермический.

Найти

1. ускорение поршня в начальный момент времени

2. уравнение колебаний поршня x = x(t) , x₀ < l₀

Решение

1. l₀

   l₀

   Объем газа в левой и правой части

x

l₀ - x

l₀ + x

x

2. Сила, действующая на поршень

при x₀ << l₀ можно пренебречь x²

3. Уравнение движения

4. Ускорение поршня в начальный момент времени

Билет 11 №3 Капли дождя падают на тележку m₀ = 4 кг, ₀ = 20 м/c , α = 60° ,  = 58 грамм/с.

Найти зависимость скорости тележки u(t) , если t = 0, u₀ = 0.

Решение

За время dt на тележку упадет dt воды со скоростью .

Билет 11 №4 Два проводника с токами I₁ и I₂ скрещиваются на расстоянии L.

Дано : I₁ = 1А, I₂ = 8А, L = AB = 10 см .

Найти точку с минимальным H.

I₂

L

I₁

x

Билет 12 №3 Два проводника расположены в горизонтальной плоскости на расстоянии d₀ = 20 см. На проводнике лежат 2 перемычки m = 40 гр каждая, R = 0,02 Ом, B = 0,2 Тл, a = 0,1 м/с2 .

Найти скорость 2й перемычки u = u(t).

B

m

m

Н

a

айти скорость 2й перемычки u = u(t).

Решение