25 Вопрос

математическое ожидание некоторых функций от случайных аргументов

Математическим ожиданием случайной величины Хназывается число

   (4) т.е. математическое ожидание случайной величины – это взвешенная сумма значений случайной величины с весами, равными вероятностям соответствующих элементарных событий.

26 Вопрос Ковариация, коэффициент корреляции.

Особую роль играет центральный момент порядка 1+1 или второй смешанный центральный момент, который называется ковариацией или корреляционным моментом m_1,1(x, y) = K_{xy=   (11.8)}

 Ковариация представляет собой математическое ожидание произведения центрированных случайных величин X и Y и характеризует степень линейной статистической зависимости величин X и Y и рассеивание относительно точки (m_x, m_y):

K_xy = , 

Свойства коэффициента корреляции:

1. Абсолютная величина коэффициента корреляции двух случайных величин не превышает единицы: 

2. │r_xy│=1 если Y=aХ+b

27 Вопрос Свойства дисперсии

Свойства дисперсии следуют из соответствующих свойств математического ожидания. Заметим, что из существования второго момента следует существование математического ожидания случайной величины и конечность дисперсии.

Во всех свойствах ниже предполагается существование вторых моментов случайных величин.

D1.

 Дисперсия может быть вычислена по формуле:  .

Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

D[Х] = М[(Х – М[Х])²].                           

28 Вопрос средняя арифметическая простая и взвешенная.

Если имеется несколько различных индивидуальных величин одного и того же вида и надо исчислить среднюю, то необходимо найти сумму всех индивидуальных величин и поделить полученную сумму на их число.

Обозначим индивидуальные значения признака через x1, x2, x3, ...xn, число индивидуальных величин - n, среднюю величину - .

Средняя величина, вычисленная по формуле:

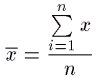
называется средней арифметической простой.

Средняя арифметическая простая равна частному от деления суммы индивидуальных значений признака на их количество.

29 Вопрос Состоятельная оценка неизвестного параметра с в

Состоятельной называют статистическую оценку, кото­рая при n—» стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при п—»о стремится к нулю, то такая оценка оказы­вается и состоятельной.

30 Вопрос

• Несмещенность.

       Оценка параметра   называется несмещенной, если ее математическое ожидание равно  , в противном случае оценка называется смещенной.  Требование несмещенности очень важно при малом количестве опытов.

Итак, статистической оценкой неизвестного пара­метра теоретического распределения называют функцию от наблюдаемых случайных величин. ^ Несмещенные, эффективные и состоятельные оценки. Для того чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров, они должны удовлетворять определенным требованиям. Ниже указаны эти требования.

Несмещенной называют статистическую оценку *, мате­матическое ожидание которой равно оцениваемому пара­метру  при любом объеме выборки, т. е. M (*) = . Смененной называют оценку, математическое ожидание которой не равно оцениваемому параметру.