9 Ответ

Формула Байеса.

Следствием правила умножения, и формулы полной вероятности является теорема гипотез или формула Байеса.

По условиям опыта известно, что гипотезы   несовместны, образуют полную группу событий:

 Ø при   и  .

Вероятности гипотез до опыта (так называемые «априорные вероятности») известны и равны

; 

Предположим, что опыт произведен и в результате появилось событие A. Спрашивается, как нужно пересмотреть вероятность гипотез с учетом этого факта, или, другими словами, какова вероятность того, что наступлению события A предшествовала гипотеза  (послеопытные вероятности называются апостериорными):

.

Вероятность наступления события A совместно с гипотезой H_k определяется с использованием теоремы умножения вероятностей:

P(AÇH_k)=P(H_k)×P(A/H_k)=P(A)×P(H_k/A). (3.6)

Таким образом, можно записать:

P (H_k/A) =P (H_k) ×P (A/H_k)/P (A). (3.7)

С использованием формулы полной вероятности

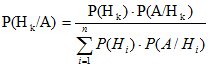. (3.8)

Формула (3.8) называется формулой Байеса. Она позволяет пересчитывать вероятности гипотез в свете новой информации, состоящей в том, что опыт дал результат А

10 Ответ (схема Бернулли)

Под схемой Бернулли понимают конечную серию   повторных независимых испытаний с двумя исходами. Вероятность появления (удачи) одного исхода при одном испытании обозначают  , а непоявления (неудачи) его  . Я. Бернулли установил, что вероятность ровно   успехов в серии из   повторных независимых испытаний вычисляется по следующей формуле:

То значение  , при котором число   является максимальным из множества { }, называется наивероятнейшим, и оно удовлетворяет условию

np - q   m  np+ p, 

Формулу Бернулли можно обобщить на случай, когда при каждом испытании происходит одно и только одно из   событий с вероятностью   (  . Вероятность появления   раз первого события и   - второго и  -го находится по формуле

При достаточно большой серии испытаний формула Бернулли становится трудно применимой, и в этих случаях используют приближенные формулы. Одну из них можно получить из предельной теоремы Пуассона:

Таблица значений функции  имеется в приложении 3.

20 Вопрос Законы распределения непрерывных случайных величин

Закон распределения непрерывной случайной величины нельзя задать также, как для дискретной. Он неприменим в силу того, что нельзя перечислить все бесконечное несчетное множество значений, а вероятности каждого отдельно взятого значения непрерывной случайной величины равны нулю.

Для описания закона распределения непрерывной случайной величины Х предлагается другой подход: рассматривать не вероятности событий Х=х для разных х, а вероятности события Х<х. При этом вероятность P(X<x) зависит от текущей переменной, т. е. является некоторой функцией от х.

Функцией распределения случайной величины Х называется функция F(x), выражающая для каждого х вероятность того, что случайная величина Х примет значение, меньшее х:

.

Функцию F(x) называют интегральной функцией распределения или интегральным законом распределения.