
- •23. Электрическая емкость. Конденсаторы
- •25. Сторонние электродвижущие силы
- •24. Энергия взаимодействия электрических зарядов
- •26. Законы электрического тока. Законы Кирхгофа.
- •2 9. Вывод законов Ома и Джоуля – Ленца в классической теории электронной проводимости металлов.
- •31. Ток в электролитах. Электролиз. Законы Фарадея
- •33. Топливный элемент
2 9. Вывод законов Ома и Джоуля – Ленца в классической теории электронной проводимости металлов.
j = enu.
За время t
электрон может приобрести среднюю
скорость направленного движении
u
= at
=
= enu.
За время t
электрон может приобрести среднюю
скорость направленного движении
u
= at
=
г де
a
= F/m
= eE/m
-
ускорение, сообщаемое электрону силой
F
= = eE.
Среднее значение скорости u
де
a
= F/m
= eE/m
-
ускорение, сообщаемое электрону силой
F
= = eE.
Среднее значение скорости u
 Подставив
величину
uср
в выражение для плотности тока получим
Плотность
тока
пропорциональна
Подставив
величину
uср
в выражение для плотности тока получим
Плотность
тока
пропорциональна
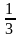
 напряженности
поля, что соответст -вует закону Ома j
= sE,
s-величина
электропроводности,
равная l
= nvCV
l,
l-Коэффициент
напряженности
поля, что соответст -вует закону Ома j
= sE,
s-величина
электропроводности,
равная l
= nvCV
l,
l-Коэффициент
 теплопроводности
для металлов.
теплопроводности
для металлов.
Разделив l на s, имеем (mv2 » 3kT) .
- закон Видемана -
Франца, утверждающий, что отношение
коэффициента теплопроводности l
для металлов к удельной электропроводности
s
пропорционально
температуре и не зависит от рода металла.
Классическая
теория
электропроводности дает правильное
объяснение закону Джоуля -
Ленца, т.е. тепловому действию тока.
Поскольку
при каждом столкновении частицей
рассеивается дополнительно приобретенная
энергия mu2/2,
а число таких столкновений в единице
объема равно n/t
, то полное тепловыделение в единице
объема =sЕ2
закон Видемана -
Франца, утверждающий, что отношение
коэффициента теплопроводности l
для металлов к удельной электропроводности
s
пропорционально
температуре и не зависит от рода металла.
Классическая
теория
электропроводности дает правильное
объяснение закону Джоуля -
Ленца, т.е. тепловому действию тока.
Поскольку
при каждом столкновении частицей
рассеивается дополнительно приобретенная
энергия mu2/2,
а число таких столкновений в единице
объема равно n/t
, то полное тепловыделение в единице
объема =sЕ2
Удельная мощность тока w пропорциональна квадрату электрического поля и удельной электропроводности
Сопротивление однородного проводника R = rl/S ; l и S – его длина и поперечное сечение; r - удельное сопротивление вещества проводника, определяемое удельной электропроводностью r=1/s.R = R0(1 + at), R0 – сопротивление при 0 °С и a – температурный коэффициент сопротивления.
30. Сверхпроводимость Несоответствие поведения электронов в металле предсказаниям классической теории электропроводности обусловлено тем, что в металле электрон ведет себя как квантовый объект. Поэтому для описания поведения электронов в металлах необходимо использовать уравнение Шрёдингера.В рамках квантовый механики удаётся объяснить одно из интереснейших явлений: явление сверхпроводимости металлов. в твердых телах при температуре перехода в сверхпроводящее состояние Тс – критической температуре, между электронами начинают действовать силы притяжения, обусловленные обменом фононами между электронами.Фононы – кванты упругих колебаний кристаллической решетки. Это притяжение приводит к образованию связанных электронных пар – куперовских пар. Спаренные электроны являются бозонами – частицами с нулевым спином, и стремятся сконденсироваться. В результате такой конденсации образуется электрически заряженная, сверхтекучая электронная жидкость, обладающая свойствами сверхпроводимости. Сверхпроводящее состояние является макроскопическим квантовым состоянием металла.
