
Лабораторная работа 4 планирование многофакторных экспериментов
Важной задачей планирования эксперимента является определение числа опытов, которые необходимы для выявления зависимости между исследуемыми переменными величинами.
Те, переменные параметры, которые изменяются экспериментатором в процессе испытаний, называются факторами, а те параметры, которые изучаются или оптимизируются, называются выходами или откликами системы, или параметрами оптимизации системы.
При математическом планировании эксперимента предполагается, что существует некоторая аналитическая связь между факторами и откликом процесса, и требуется выбрать минимальное число и условия проведения опытов, позволяющих найти область оптимальных значений параметров. Другими словами необходимо найти приближенную зависимость выходного параметра от факторов, т.е. построить математическую модель процесса. Математическая задача планирования эксперимента состоит в том, чтобы найти уравнение поверхности отклика:
 (4.1)
(4.1)
где y - выход процесса, т.е. параметр оптимизации;
xi - факторы, которые варьируются при проведении эксперимента.
Таким образом, математическое планирование фактически связано с изучением формы поверхности отклика и, следовательно, оптимальному значению выхода будут соответствовать максимальные или минимальные точки этой поверхности.
Для большинства реальных задач вид поверхности отклика заранее неизвестен, поэтому при экспериментальном поиске оптимальных условий функцию у представляют в виде системного ряда:
 (4.2)
(4.2)
Очевидно, точность подобной аппроксимации определяется порядком системного ряда и диапазоном изменения переменных хi. Так как поверхность отклика изучается обычно в сравнительно узком интервале варьирования факторов, то без большой погрешности можно отбросить члены высших порядков. Задача оптимизации решается в два этапа: сначала осуществляется поиск области оптимума, для чего используется линейная модель поверхности отклика; на втором этапе для описания почти стационарной (оптимальной) области используется степенной ряд, содержащий члены второго, а иногда и третьего порядка. Коэффициенты степенного ряда b можно оценить с помощью выборочных коэффициентов регрессии b, которые определяются по результатам конечного числа опытов. Тогда уравнение регрессии, получаемое на основании результатов экспериментов, примет вид:
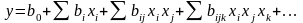 (4.3)
(4.3)
Таким образом, после вычисления коэффициентов регрессии появляется возможность оценить влияние изучаемых факторов на функцию отклика и определить направление движения к области оптимума.
В качестве выхода процесса рекомендуется выбирать параметр, который имеет ясный физический смысл и количественное выражение, при этом желательно, чтобы параметр оптимизации был единственным и не зависел от времени.
Для каждого фактора выбираются условный нулевой или основной уровень хi0, диапазон и шаг Dxi варьирования переменных. Диапазон изменения факторов равен разности между верхним и нижним пределом данного фактора.
