Завдання для самостійної роботи

Знайти інтервали монотонності функцій:

1. ;

2. ;

3. ;

4. .

1.2. Локальний екстремум функції

Точка називається точкою максимуму (або мінімуму) функції , якщо існує такий окіл < < цієї точки, який належить області визначення функції, і для всіх з цього околу виконується нерівність < (або > ).

Правило знаходження екстремумів (максимумів і мінімумів) за допомогою першої похідної:

1. знайти область визначення ;

2. знайти похідну ;

3. знайти критичні точки;

4. дослідити знак на інтервалах, на які знайдені критичні точки ділять область визначення .

При цьому критична точка є точкою мінімуму, якщо при переході через неї зліва направо змінює знак з “-” на “+”, є точкою максимуму, якщо змінює знак з “+” на “-”.

5. обчислити значення функції в точках екстремуму (екстремуми).

Зразки розв’язування задач

Знайти екстремуми функцій.

1. .

1) Область визначення .

2) .

3) Критичні точки:

.

існує для всіх .

4) Знаки :

При переході через точку похідна змінює знак з « + » на « - », отже - точка максимуму. При переході через точку похідна змінює знак з « - » на « + », тому - точка мінімуму.

5) . .

2. .

1) Область визначення функції .

2) .

3) Критичні точки:

або , звідки .

існує для всіх .

4) Знаки :

При переході через точку похідна змінює знак з « - » на « + », тому точка є точкою мінімуму. При переході через точку похідна змінює знак з « + » на « - ». Отже, точка є точкою максимуму.

5) ; .

3. .

1) Область визначення .

2) .

3) Критичні точки:

, звідки .

існує на всій області визначення.

4) Знаки :

При переході через точки похідна змінює знак з « - » на « + ». Отже, точки є точками мінімуму. При переході через точку похідна змінює знак, але , тому не є точкою екстремуму.

5) Так як функція парна, то

. Тобто .

4. .

1) .

2) .

3) Критичні точки:

.

Функція приймає тільки додатні значення, причому . Критичну точку знайдемо з умови: . Отримаємо .

існує для всіх .

4) Знаки :

Функція має дві екстремальні точки: - точка мінімуму; -точка максимуму.

5) ; .

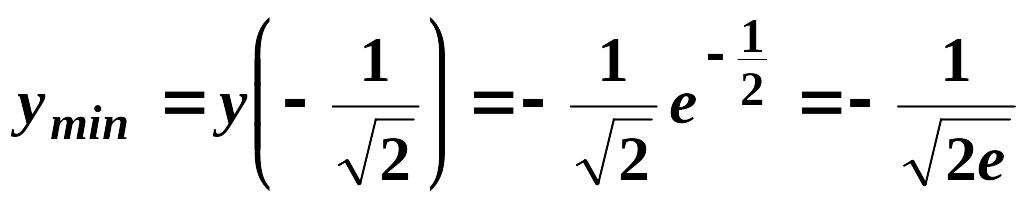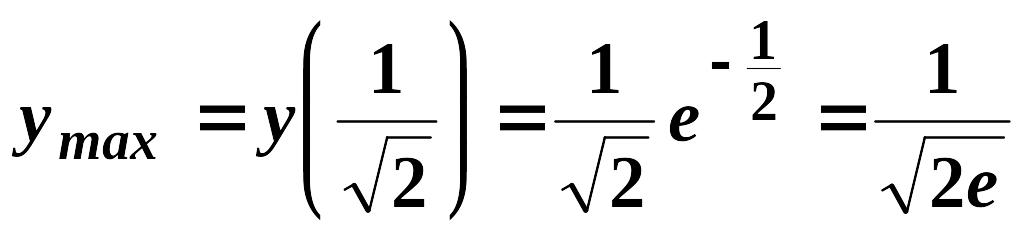5. .

1) Область визначення .

2)

.

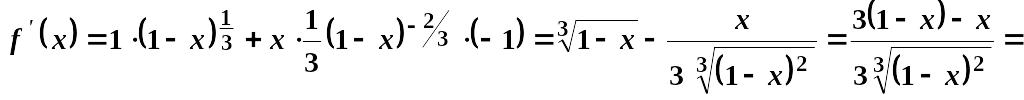
3) Критичні точки:

а) .

б) не існує при .

4) Знаки :

При переході через точку похідна змінює знак з « + » на « - », тому є точкою максимуму. При переході через точку похідна не змінює свій знак. Отже, критична точка не є екстремальною.

5) .

6. .

1) .

2) .

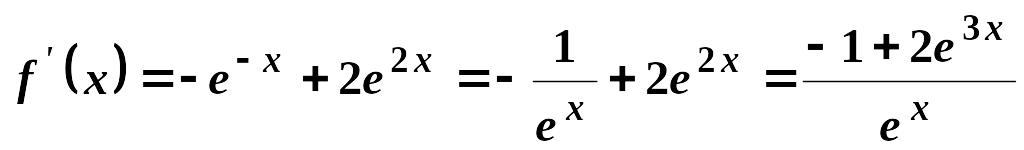3) Критичні точки:

а) , тоді , звідки або .

б) існує для всіх .

4)Знаки :

При переході через точку похідна змінює знак з « - » на « + », тому - точка мінімуму.

5) .

7. .

1) Область визначення .

2) .

3) Критичні точки:

а) , звідки . Але не входить в .

б) існує на всій області визначення.

4) Знаки :

П ри переході через точку похідна змінює знак з « - » на « + », тому - точка мінімуму.

5) .

8. .

1) Область визначення .

2) .

3) Критичні точки:

а) . Знайдемо , тому рівняння не має коренів, тобто .

б) існує на всій області визначення.

Отже, критичних точок не має і функція не має екстремумів.