
- •Расчетно-пояснительная записка к курсовой работе по дисциплине” Основы логистики”
- •Введение
- •1.Задание на курсовую работу
- •2. Методические указания по выполнению курсовой работы
- •2.1. Организация производства готовой продукции
- •2.2. Организация материально-технического снабжения производства (закупок сырья)
- •2.3. Организация сбыта готовой продукции
2.3. Организация сбыта готовой продукции
Содержательная постановка задачи. Процесс сбыта определяется соотношением между количеством подготовленных отгрузочных партий и наличием транспортных средств. В случае ограниченного режима работы транспортных средств на складе экспедиции накапливается запас готовой продукции, который затем нужно будет вывезти в течение небольшого периода времени. Иначе могут исчерпаться ресурсы складской площади в связи с поступлением новой продукции.
Быстрое реагирование на предъявленный спрос и доставка свежей продукции позволят поддержать объем продаж на достигнутом уровне, а задержка поставки, очевидно, приведет к падению спроса потребителей.
Таким образом, выбор оптимальных режимов взаимодействия в сбытовых системах должен происходить с учетом технологических особенностей процессов производства и потребления, режимов работы транспорта по критерию минимума общих логистических издержек и возможных потерь вследствие неучета указанных выше факторов.
Математическая
постановка задачи.
Обозначим через
![]() -
количество готовой продукции, отправляемое
от поставщика в i-й
период времени в j-й
пункт потребления, ед.;
-
общее количество потребителей. Будем
считать, что доставка производится
двумя завозами в период поставки (i
=
1, 2). Расстояния перевозки заданы.
-
количество готовой продукции, отправляемое
от поставщика в i-й
период времени в j-й
пункт потребления, ед.;
-
общее количество потребителей. Будем
считать, что доставка производится
двумя завозами в период поставки (i
=
1, 2). Расстояния перевозки заданы.
Тогда
суммарные затраты
![]() ,
которые необходимо свести к минимуму,
определяются из выражения:
,
которые необходимо свести к минимуму,
определяются из выражения:
![]()
![]() (3.17)
(3.17)
 при
ограничениях
при
ограничениях
![]() ;
(3.18)
;
(3.18)
![]() ;
(3.19)
;
(3.19)
![]() ;
(3.20)
;
(3.20)
 ;
(3.21)
;
(3.21)
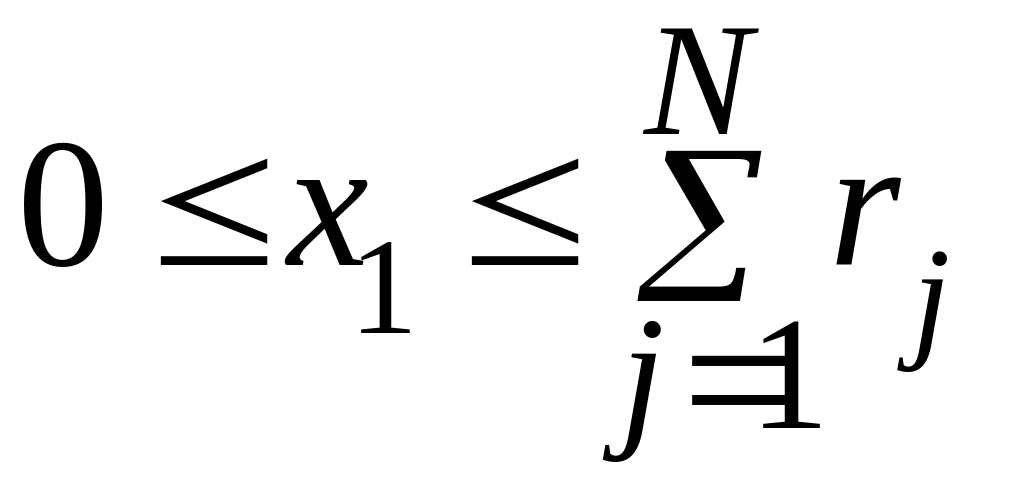 ;
(3.22)
;
(3.22)
где
![]() -
транспортные расходы по доставке
продукции на расстояние
-
транспортные расходы по доставке
продукции на расстояние
![]() от
поставщика в i-й
период времени в j-й
пункт потребления, р./км;
от
поставщика в i-й
период времени в j-й
пункт потребления, р./км;
![]() -
количество ездок (рейсов), совершаемое
автомобилем в i-й
период времени в j-й
пункт потребления;
-
количество ездок (рейсов), совершаемое
автомобилем в i-й
период времени в j-й
пункт потребления;
![]() -
штраф за задержку поставки единицы
груза в i-й
период времени в j-й
пункт потребления, р./ед.;
-
штраф за задержку поставки единицы
груза в i-й
период времени в j-й
пункт потребления, р./ед.;
![]() -
спрос на готовую продукцию в i-й
период времени в j-м
пункте, ед.;
-
спрос на готовую продукцию в i-й
период времени в j-м
пункте, ед.;
![]() - организационные сборы на доставку
продукции (уведомление о прибытии,
оформление документов, канцелярские
расходы и т.д.) в i-й
период времени в j-й
пункт потребления, р.;
- организационные сборы на доставку
продукции (уведомление о прибытии,
оформление документов, канцелярские
расходы и т.д.) в i-й
период времени в j-й
пункт потребления, р.;
![]() - запас свежей продукции, предназначенный
для первоочередного вывоза в 1-й период
времени, ед.;
- запас свежей продукции, предназначенный
для первоочередного вывоза в 1-й период
времени, ед.;
![]() -
штраф за задержку вывоза запаса свежей
продукции
от
поставщика в i-й
период времени в j-й
пункт, р./ед.;
-
штраф за задержку вывоза запаса свежей
продукции
от
поставщика в i-й
период времени в j-й
пункт, р./ед.;
![]() -
спрос на готовую продукцию в j-м
пункте потребления, ед.;
-
спрос на готовую продукцию в j-м
пункте потребления, ед.;
![]() - производственная программа выпуска
готовой продукции в 1-й и 2-й период
времени соответственно, ед.Количество
ездок
определяется
путем деления
- производственная программа выпуска
готовой продукции в 1-й и 2-й период
времени соответственно, ед.Количество
ездок
определяется
путем деления
![]() на
грузоподъемность автомобиля и округления
полученной величины до целого ……числа
в большую сторону. Организационные
сборы
на
грузоподъемность автомобиля и округления
полученной величины до целого ……числа
в большую сторону. Организационные
сборы
=
0, если
![]() ,
и
,
и  постоянны
при
постоянны
при
![]() .
Штраф
.
Штраф
![]() = 0, если
= 0, если
![]() ,
и постоянно растет с увеличением (
,
и постоянно растет с увеличением (![]() ).
Это способствует завозу продукции
потребителям в соответствии со спросом,
т.е. требует максимального реагирования
на изменяющийся спрос. Аналогично, штраф
).
Это способствует завозу продукции
потребителям в соответствии со спросом,
т.е. требует максимального реагирования
на изменяющийся спрос. Аналогично, штраф
![]() = 0, если
= 0, если
![]() ,
и также растет с ростом (
,
и также растет с ростом (![]() ).
Это, в свою очередь, регламентирует
своевременный вывоз запаса свежей
продукции от поставщика, равномерно
распределенного по N
потребителям.
).
Это, в свою очередь, регламентирует
своевременный вывоз запаса свежей
продукции от поставщика, равномерно
распределенного по N
потребителям.
Обозначим
через
![]() суммарные затраты при использовании
оптимальной политики обслуживания j
потребителей.
Тогда оптимальное решение можно получить
с помощью рекуррентных соотношений
суммарные затраты при использовании
оптимальной политики обслуживания j
потребителей.
Тогда оптимальное решение можно получить
с помощью рекуррентных соотношений
![]() ,
(3.23)
,
(3.23)
где
![]() удовлетворяет условиям
удовлетворяет условиям
; (3.24)
 .
(3.25)
.
(3.25)
Переменная
х1
в (3.23) изменяется от 0 до
![]() при начальном условии:
при начальном условии:
![]() .
.
Решая (3.23) с учетом ограничений (3.24) и (3.25), можно получить оптимальное количество продукции, которое нужно доставить от поставщика в i-й период времени в j-й пункт потребления.
Задание. Обслуживается 5 потребителей. Готовая продукция потребителям доставляется грузовыми единицами, равными 500 кг. Перевозка осуществляется . автомобилями грузоподъемностью 5 т, т.е. единовременно может перевозиться 10 ед. Расстояния от отправителя до потребителей представлены в табл. 2.9.
Таблица 2.9
Расстояния до потребителей
j
1
2
3
4
5
lij,
км
5
4
9
11
13
Спрос и производительность (производственная программа выпуска) по периодам приведены в табл. 2.4.
Решение. Спрос у потребителей для 1-го периода составляет r1 = 12 т, производственная программа выпуска у производителя в этом периоде равна спросу и составляет также z1 = 12 т. Так как размер грузовой единицы составляет 500 кг, то всего необходимо доставить потребителям 66 ед. Распределение спроса по завозам представлено в табл. 2.10.
Спрос
по первому завозу, согласно табл. 2.10,
соответствует производственной программе
![]() 32
ед. Будем считать, что запас свежей
продукции усв
составляет
50 % от х1
, и равен соответственно 16 ед.
32
ед. Будем считать, что запас свежей
продукции усв
составляет
50 % от х1
, и равен соответственно 16 ед.
Распределение
спроса в единицах продукции по завозам
j
1
2
3
4
5
Итого
1
завоз
5
10
3
6
8
32
2 завоз
7
5
7
11
4
34
rj
12
15
10
17
12
66
![]() =
45 р./ед. и
=
45 р./ед. и
![]() =
90 р./ед. Таблица 2.10
=
90 р./ед. Таблица 2.10
Для
1-го потребителя суммарный спрос
составляет 18 ед., спрос по периодам -
![]() =
5
ед. и
=
5
ед. и
![]() =
7
ед., поэтому
при х1
= 0 и х11
= 0; х21
=12
– 0 =12 количество
ездок составит соответственно:
=
7
ед., поэтому
при х1
= 0 и х11
= 0; х21
=12
– 0 =12 количество
ездок составит соответственно:![]() =0/5=0,
=0/5=0,
![]() =12/5
≈ 3.
=12/5
≈ 3. Отсюда
следует, что:
Отсюда
следует, что:
f1(0 - 0) = f1(1 - 0) = … = f1(70 - 0) = 2*10*5*0+64*(3-0)+15+45*
*(16/5-0)+2*10*5*2+64*(6-0)+15+9*(16/5-90)= 794 р.
При х1 = 1 и х11 = 1, х21 = 12– 1 = 11 количество ездок составит: = 1/5 ≈ 1,
 =11/5
≈ 3, поэтому
f1(1
- 1) = f1(2
- 1) = … = f1(70
- 1) = 2*10*5*1+64*
=11/5
≈ 3, поэтому
f1(1
- 1) = f1(2
- 1) = … = f1(70
- 1) = 2*10*5*1+64*
*(3-1)+15+45*(16/5-1)+2*10*5*2+64*(6-8)+15+90*(16/5-8) = 785р.
Аналогично рассчитываются значения f1(x1) при изменении x1 от 0 до 70. Полученные результаты заносятся в табл. 2.11.
Таблица 2.11
Значения функции f1(x1)
j |
x1 |
х11 |
x21 |
f1(x1) |
j |
x1 |
x11 |
x21 |
f1(x1) |
j |
x1 |
x11 |
x21 |
f1(x1) |
1 |
0 |
0 |
12 |
794 |
1 |
7 |
6 |
6 |
494 |
1 |
12 |
0 |
12 |
794 |
1 |
1 |
0 |
12 |
794 |
1 |
7 |
7 |
5 |
458 |
1 |
12 |
1 |
11 |
785 |
1 |
1 |
1 |
11 |
785 |
1 |
8 |
0 |
12 |
794 |
… |
… |
… |
… |
… |
1 |
2 |
0 |
12 |
794 |
1 |
8 |
1 |
11 |
785 |
1 |
12 |
5 |
7 |
330 |
1 |
2 |
1 |
11 |
785 |
… |
… |
… |
… |
… |
… |
… |
… |
… |
…. |
1 |
2 |
2 |
10 |
576 |
1 |
8 |
5 |
7 |
330 |
1 |
12 |
11 |
1 |
1012 |
1 |
3 |
0 |
12 |
794 |
… |
… |
… |
… |
…. |
1 |
12 |
12 |
0 |
1066 |
1 |
3 |
1 |
11 |
785 |
1 |
8 |
7 |
5 |
458 |
1 |
13 |
0 |
12 |
794 |
1 |
3 |
2 |
10 |
576 |
1 |
8 |
8 |
4 |
522 |
1 |
13 |
1 |
11 |
785 |
1 |
3 |
3 |
9 |
467 |
1 |
9 |
0 |
12 |
794 |
… |
… |
… |
… |
… |
1 |
4 |
0 |
12 |
794 |
1 |
9 |
1 |
11 |
785 |
1 |
13 |
5 |
7 |
330 |
1 |
4 |
1 |
11 |
785 |
… |
… |
… |
… |
… |
… |
… |
… |
… |
…. |
1 |
4 |
2 |
10 |
576 |
1 |
9 |
5 |
7 |
330 |
1 |
13 |
12 |
0 |
1066 |
1 |
4 |
3 |
9 |
467 |
… |
… |
… |
… |
… |
1 |
13 |
12 |
0 |
1066 |
1 |
4 |
4 |
8 |
394 |
1 |
9 |
8 |
4 |
522 |
|
|
|
|
|
1 |
5 |
0 |
12 |
794 |
1 |
9 |
9 |
3 |
604 |
|
|
|
|
|
1 |
5 |
1 |
11 |
785 |
1 |
10 |
0 |
12 |
794 |
|
|
|
|
|
… |
… |
… |
… |
… |
1 |
10 |
1 |
11 |
785 |
|
|
|
|
|
1 |
5 |
4 |
8 |
394 |
… |
… |
… |
… |
… |
|
|
|
|
|
1 |
5 |
5 |
7 |
330 |
1 |
10 |
5 |
7 |
330 |
|
|
|
|
|
1 |
6 |
0 |
12 |
794 |
… |
… |
… |
… |
… |
|
|
|
|
|
1 |
6 |
1 |
11 |
785 |
1 |
10 |
9 |
3 |
604 |
|
|
|
|
|
… |
… |
… |
… |
|
1 |
10 |
10 |
2 |
758 |
|
|
|
|
|
1 |
6 |
5 |
7 |
330 |
1 |
11 |
0 |
12 |
794 |
|
|
|
|
|
1 |
6 |
6 |
6 |
494 |
1 |
11 |
1 |
11 |
785 |
|
|
|
|
|
1 |
7 |
0 |
12 |
794 |
… |
… |
… |
… |
… |
|
|
|
|
|
1 |
7 |
1 |
11 |
785 |
1 |
11 |
5 |
7 |
330 |
|
|
|
|
|
1 |
7 |
2 |
10 |
576 |
… |
… |
… |
… |
… |
|
|
|
|
|
… |
… |
… |
… |
…. |
1 |
11 |
10 |
2 |
758 |
|
|
|
|
|
1 |
7 |
5 |
7 |
330 |
1 |
11 |
11 |
1 |
1012 |
|
|
|
|
|
 Для
2-го потребителя суммарный спрос
составляет 7 ед., спрос по периодам -
Для
2-го потребителя суммарный спрос
составляет 7 ед., спрос по периодам -
![]() =
10
и
=
10
и
![]() =
5.
=
5.
При
х1
= 0 и
х12
= 0,
х22
= 16 – 0 = 16
количество ездок составит:
![]() = 0/5 = 0,
= 0/5 = 0,
![]() =
15/5 ≈ 3, поэтому
=
15/5 ≈ 3, поэтому
![]() 2*10*9*0+64*(10-0)+15+45*(16/5-0)+2*10*9*3+64*
2*10*9*0+64*(10-0)+15+45*(16/5-0)+2*10*9*3+64*
*(5-15)+15+90*(16/5-5)+794 = 1848 р.
Аналогично рассчитываются значения для различных j от 2 до 5 при изменении х1 от 0 до 50. Полученные результаты заносятся в табл. 2.12.
Таблица 2.12
Значения функции
-
j
x1
x1j
x2j
fj(x1)
j
x1
x1j
х2j
fj(x1)
j
x1
x1j
x2j
fj(x1)
1
0
0
9
794
2
35
5
10
9
 20
204
4
4
1
 2
22800
1
1
0
9
785
2
2

 4
45
10
920
4
5
5
11
2412
1
2
2
7
576
…
…
…
…
…
4
6
5
11
2412
1
3
3
6
467
2
70
5
10
920
…
…
…
…
…
1
4
4
5
394
3
0
0
9
2574
4
59
5
11
2412
1
5
5
4
330
3
1
0
9
2607
4
5
 3
35
13
2412
1
6
5
4
330
3
2
2
7
2180
…
…
…
…
…
1
7
5
4
330
3
3
3
6
1853
4
70
5
11
2412
1
8
5
4
330
3
4
4
5
1762
5
0
0
7
5478
…
…
…
…
…
3
5
5
4
1438
5
1
0
7
5773
1
20
5
4
330
3
6
5
4
1438
5
2
2
8
4648
1
9


5
8
330
3
7
5
4
1438
5
3
3
7
4103
…
…
…
…
…
3
8
5
3
1438
5
4
4
6
3866
1
70
5
4
330
3
9
5
3
1438
5
5
5
5
3414
2
0
0
15
1848
3
10
5
3
1438
5
6
5
5
3414
2
1
0
15
1810
…
…
…
…
…
5
7
5
5
3414
2
2
2
13
1492
3
3
 5
55
6
1438
5
8
5
5
3414
2
3
3
12
1274
…
…
…
…
…
…
…
…
…
…
2
4
4
11
1128
3
70
5
3
1438
5
17
5
5
3414
2
5
5
10
920
4
0
0
16
4012
5
18
5
5
3414
2
6
5
10
920
4
1
0
16
4156
5
19
5
5
3414
2
7
5
10
920
4
2
2
14
3400
…
…
…
…
…
…
…
…
…
…
4
3
3
13
2964
5
6
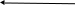 6
65
8
3414
 Минимальные
затраты при оптимальной политике сбыта
составят f5(x1)
= 2802 р. Используя данные табл. 3.12 и двигаясь
в обратном направлении, т.е. от 6-го до
1-го потребителя, получаем план сбыта
на 1-й период. Например, функции f5(70)
по табл. 3.12 соответствуют значения x15
= 5; x25
= 5. На следующих шагах принимаем f4(60)
и получаем соответственно x14
= 5;
Минимальные
затраты при оптимальной политике сбыта
составят f5(x1)
= 2802 р. Используя данные табл. 3.12 и двигаясь
в обратном направлении, т.е. от 6-го до
1-го потребителя, получаем план сбыта
на 1-й период. Например, функции f5(70)
по табл. 3.12 соответствуют значения x15
= 5; x25
= 5. На следующих шагах принимаем f4(60)
и получаем соответственно x14
= 5;
x24 = 11, и т.д. Оптимальное распределение завоза продукции потребителям в 1-й периоде представлено в табл. 2.13.
Таблица 2.13
Оптимальное распределение готовой продукции
№ |
1 завоз, ед. |
2 завоз, ед. |
Месячная |
||
потребителя |
план |
оптим. |
план |
оптим. |
потребность, ед. |
1 |
5 |
5 |
7 |
7 |
12 |
2 |
10 |
5 |
5 |
10 |
15 |
3 |
3 |
5 |
7 |
5 |
10 |
4 |
6 |
5 |
11 |
12 |
17 |
5 |
8 |
5 |
4 |
7 |
12 |
Сумма |
32 |
25 |
34 |
41 |
66 |
Аналогично определяется оптимальное распределение готовой продукции по потребителям в остальные периоды времени.
 СОДЕРЖАНИЕ
СОДЕРЖАНИЕ
Введение
1.Задание на курсовую работу…………………………………………5
2.Методические указания по выполнению курсовой работы………………………………………………………………….……6
2.1 Организация производства готовой продукции………………………………………………………………..6
2.2 Организация материально-технического снабжения
производства (закупок сырья)………………………………………...11
2.3 Организация сбыта готовой продукции…………………………18
Заключение ……………………………………………………………..25
Список используемой литературы…………………………………….26
 Список
используемой литературы
Список
используемой литературы
1. Основы логистики: Учебное пособие / Под ред. проф. Л.Б. Миротина и проф. В.И.Сергеева.- М.: ИНФРА-М, 1999.- 200 с.
2. Транспортная логистика: Учебное пособие для автотранспортных вузов / Под ред. проф. Л.Б.Миротина.- М.: МГАДИ(ТУ), 1996.- 211 с.
3. Пилишенко А.Н. Логистика: Практикум / Под ред. д-ра экон. наук проф. Н.К.Моисеевой.- М.: МИЭТ, 1998.- 172 с.
4. Гордон М.П., Карнаухов С.Б. Логистика товародвижения. – М.: Центр экономики и маркетинга, 1998.- 168 с.
5. Мельник М.М. Экономико-математические методы в материально-техническом снабжении.- М., 1990.- 325 с.
6. Беллман Р, Дрейфус С. Прикладные задачи динамического программирования. – М.: Наука, 1965. – 458 с.
7. Исследование операций в экономике / Под ред. Н.Ш. Кремера. – М.: Банки и биржи, ЮНИТИ, 1997. – 407 с.
8. Калихман И.Л., Войтенко М.А. Динамическое программирование в примерах и задачах. – М.: Высшая школа, 1979. – 125 с.

Заключение
На основе приведенных расчетов можно сделать некоторые выводы:
По пункту 2.1. установили оптимальную производственную программу на год.
k |
1 |
2 |
3 |
4 |
5 |
6 |
rk, т |
33 |
29 |
41 |
28 |
28 |
24 |
zk, т |
33 |
29 |
41 |
28 |
28 |
24 |
По пункту 2.2 определили оптимальные объемы поставок сырья в течение года.
t |
Спрос , т |
Текущий уровень запаса , т |
Объем поставки , т |
Затраты нарастающим итогом, р. |
1 |
33 |
17 |
0 |
817,7 |
2 |
29 |
8 |
20 |
25767,7 |
3 |
41 |
7 |
40 |
78107,6 |
4 |
28 |
19 |
40 |
103497,7 |
5 |
28 |
21 |
30 |
126599,7 |
6 |
24 |
27 |
30 |
146449,5 |
По пункту 2.3 получили оптимальное количество продукции, которое нужно доставить от поставщика в i-й период времени в j-й пункт потребления.
№ |
1 завоз, ед. |
2 завоз, ед. |
Месячная |
||
потребителя |
план |
оптим. |
план |
оптим. |
потребность, ед. |
1 |
5 |
5 |
7 |
8 |
12 |
2 |
10 |
5 |
5 |
10 |
15 |
3 |
3 |
5 |
7 |
6 |
10 |
4 |
6 |
5 |
11 |
13 |
17 |
5 |
8 |
5 |
4 |
8 |
12 |
сумма |
32 |
25 |
34 |
45 |
66 |
