Лабораторная работа № 8 математический и физический маятники

Цель работы: изучение колебаний математического и физического маятников; определение ускорения свободного падения.

Теоретическая часть

Рис. 8.1.

Простейшим примером гармонических колебаний является движение так называемого математического маятника. Математическим маятником называется маятник, состоящий из материальной точки массой m, подвешенной на невесомой нерастяжимой нити длиной и колеблющейся около точки подвеса О. В этом случае центр тяжести системы можно считать совпадающим с центром тяжести груза. Напишем уравнение движения для математического маятника, находящегося в поле тяготения и отклоненного от состояния равновесия на угол . Система, выведенная из состояния устойчивого равновесия и предоставленная самой себе, совершает колебания, называемые свободными. На маятник в отклоненном состоянии действует составляющая силы тяжести (рис. 8.1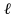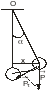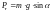) . Она направлена по касательной к траектории груза в сторону положения равновесия. Уравнение движения груза будет иметь вид:

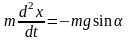. (8.1)

В этой записи уравнения учтено, что возвращающая сила всегда направлена в сторону, противоположную направлению возрастания смещения х. При малых отклонениях маятника от положения равновесия (угол  не превышает 5–6 град.) можно считать, что 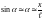, т.е. смещение по дуге можно считать приближенно равным смещению вдоль горизонтальной хорды. Уравнение (7.1) обычно записывается в виде:

, (8.2)

где: – циклическая частота гармонических колебаний.

Решением этого дифференциального уравнения является выражение: . Период колебаний маятника определяется формулой:

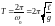. (8.3)

Из этой формулы видно, что период колебаний математического маятника зависит только от ускорения силы тяжести в данном месте Земли и от длины маятника, и не зависит от амплитуды колебаний и от массы груза. Измеряя Т и используя формулу (8.3), можно вычислить ускорение свободного падения в данном месте земной поверхности.

Рис.8.2.

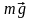Э тим методом впервые было измерено значение g на разных широтах земного шара, в результате чего была установлена зависимость g от широты . Если измерить для нескольких значений соответствующие периоды колебаний (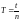 , где t − время n полных колебаний), затем построить график зависимости Т² от , то согласно формуле (7.3) эта зависимость может быть представлена в виде прямой типа: 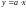. Тангенс угла наклона этой прямой численно равен: 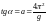. Отсюда можно найти ускорение свободного падения: .

Другой колебательной системой, с помощью которой можно определить ускорение свободного падения, является физический маятник. Физическим маятником называется твердое тело, совершающее под действием силы тяжести колебания относительно неподвижной оси, проходящей через точку О, не совпадающую с центром масс С тела (рис. 8.2).

Из-за наличия трения часть механической энергии маятника рассеивается в виде тепла, поэтому колебания всегда затухают. Так как маятник совершает вращательные колебания, то они описываются основным уравнением динамики вращательного движения относительно неподвижной оси:

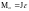, (8.4)

где: 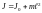– момент инерции маятника относительно оси, проходящей через точку О; J₀ – его момент относительно центра масс; - расстояние от точки О до центра масс С; m – масса маятника; – угловое ускорение; М_ – проекция на ось вращения результирующего момента всех сил, действующих на тело. Результирующий момент сил складывается из вращательного момента, создаваемого силой тяжести , и тормозящего момента, создаваемого силами трения , где k – коэффициент затухания, – угловая скорость. Знак «–» в формуле для вращательного момента отражает тот факт, что возвращающая сила всегда направлена к положению равновесия, а в формуле для тормозящего момента то, что сила трения направлена против направления движения.

При малых углах отклонения 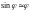, тогда 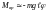, и уравнение (8.4) можно представить в виде:

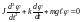. (8.5)

Введя обозначения: 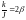, где:  – коэффициент затухания; , где: ₀ – собственная частота маятника, получаем универсальный вид дифференциального уравнения свободных затухающих колебаний:

, (8.6)

его решением является функция:

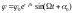, (8.7)

где: – частота свободных затухающих колебаний, – начальная фаза.

Период свободных затухающих колебаний можно найти по формуле:

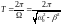. (8.8)

Если считать, что затухание колебаний мало (см. конструкцию прибора), то им можно пренебречь в выражении (8.8). Учитывая, что 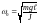получаем для периода колебаний физического маятника следующую формулу:

. (8.9)

где 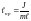– приведенная длина физического маятника. Приведенная длина физического маятника – это длина такого математического маятника, период колебаний совпадает с периодом данного физического маятника.

Точка на прямой, соединяющей точку подвеса с центром масс, лежащая на расстоянии приведенной длины от оси вращения, называется центром качания физического маятника ( см.точку О' на рис 8.2). При подвешивании маятника в центре качания О' приведенная длина, а значит, и период колебаний будут теми же, что и вначале. Следовательно, точка подвеса и центр качания обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания. На этом свойстве основано определение ускорения свободного падения с помощью так называемого оборотного маятника. Оборотным маятником называется такой маятник, у которого имеются две параллельные друг другу, закрепленные вблизи его концов опорные призмы, за которые он может поочередно подвешиваться. Вдоль маятника могут перемещаться и закрепляться на нем тяжелые грузы. Перемещением грузов добиваются того, чтобы при подвешивании маятника за любую из призм период колебаний был одинаков. Тогда расстояние между опорными ребрами призм будет равно 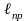. Тогда значение ускорения свободного падения можно найти по формуле:

. (8.10)