Задание для контрольной работы

Прежде чем решать задачи необходимо подставить в условие значения ваших параметров: m – ваш личный номер в студенческом билете (зачетной кгижке), N=1

Элементы линейной алгебры и аналитической геометрии

1. Даны матрицы Найти их сумму произведение AB и разность A - B.

2. Записать систему в матричной форме

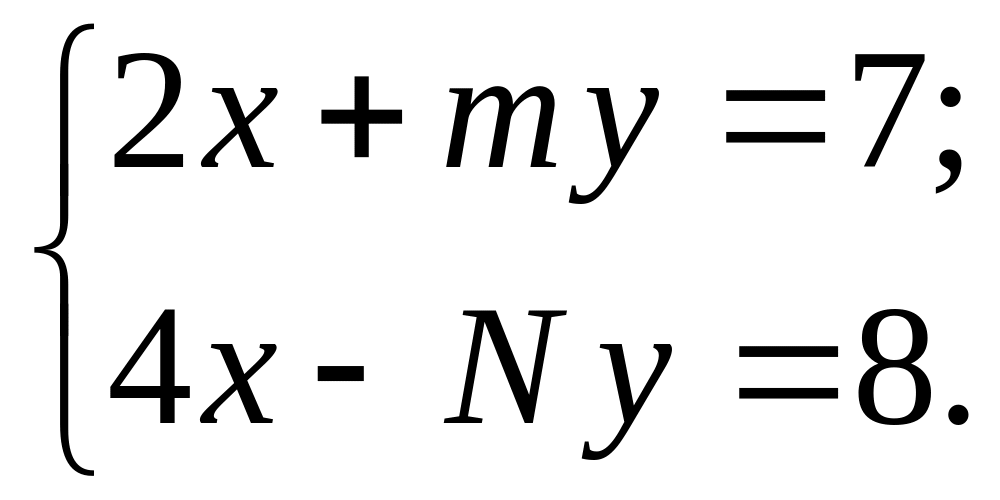
3. Вычислить определитель .

4. Решить систему с помощью метода Крамера и метода Гаусса

Элементы математического анализа

5. Найти точки экстремума данной функции:

6. Найти наибольшее и наименьшее значения функции в заданном интервале:

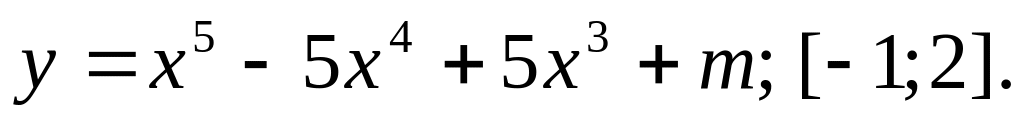
7. Найти экстремум функции двух переменных

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ДЛЯ ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ

I. Элементы линейной алгебры и аналитической геометрии

1.1.Матрицы и определители.

Матрицей называется прямоугольная таблица, в которую могут быть записаны числа или символы.

Примеры.

Элементы матрицы в общем виде записываются как , где i – номер строки, а j - номер столбца.

1.2.Действия над матрицами.

1. Сложение.

Складывать можно только матрицы одинаковых размеров. При этом нужно сложить элементы матриц, стоящие на одинаковых местах.

Пример. .

б) Умножение матрицы на число.

На данное число умножается каждый элемент матрицы.

Пример.

в) Умножение матриц.

Матрицы А и В можно перемножить, если число столбцов в матрице А равно числу строк в матрице В. При умножении получается матрица с элементами , которые равны сумме произведений элементов i-ой строки из первой матрицы на элементы j-ого столбца из второй матрицы.

Пример 1.

Пример 2. Предприятие выпускает продукцию трех видов P1, P2, P3 и использует сырье двух типов. Нормы расходов сырья заданы таблицей 1. План выпуска продукции задан таблицей 2. Найти необходимое количество сырья каждого типа.

	S1	S2		P1	P2	P3
P1	2	3		100	80	130
P2	5	2			Табл.2
P3	1	4
	Табл.1

Решение. Перемножаем матрицы

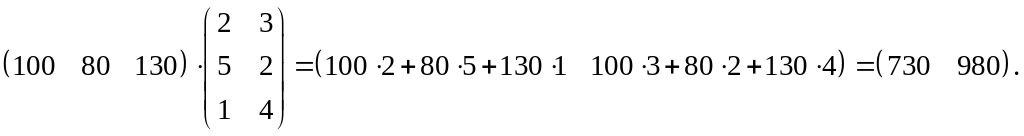
Ответ. Сырья первого типа нужно 730 единиц, а второго – 980 единиц.

Определители матриц. Для матрицы ее определитель обозначается как

Определителем второго порядка называется число

Пример.

Определителем третьего порядка называется число

Чтобы запомнить порядок перемножения и расстановки знаков используется схема

+

-

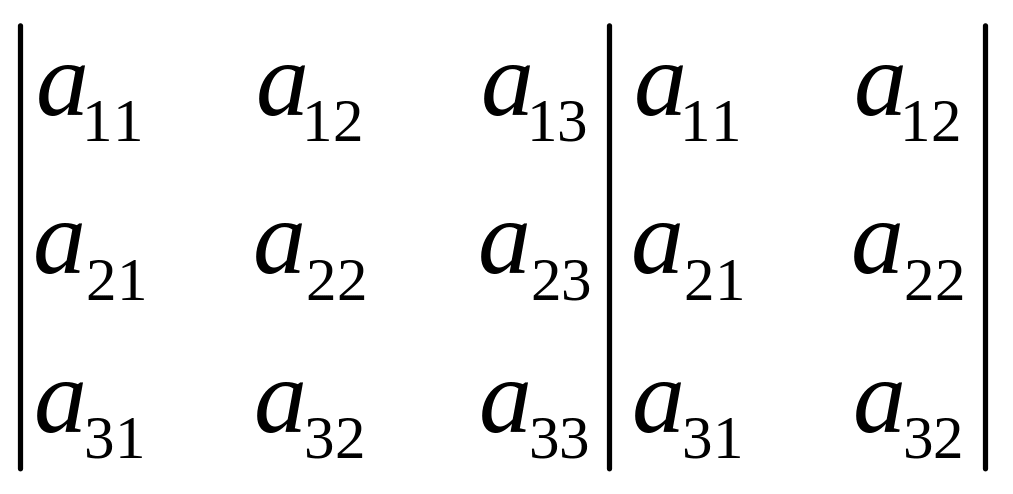
Числа, стоящие на прямых отмеченных пунктиром перемножаются. Произведения чисел на прямых со знаком (+) берутся с их знаком, произведения чисел на прямых со знаком (-) берутся с противоположным.