Многочлены Лежандра

Ортогональные полиномиальные функции Лежандра

можно получить, воспользовавшись следующим рекуррентным соотношением:

(2.7.14)

где и Эти функции ортогональны в интервале

Приведем несколько первых многочленов Лежандра:

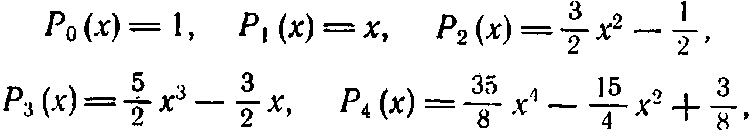
где функции _и заданы, а функции _, и получены по формуле (2.7.14). Эти функции ортогональны относительно весовой функции

и(х)= 1.

Многочлены Лагерра

Для получения многочленов Лагерра можно воспользоваться рекуррентным соотношением

где ^{и .} Эти многочлены ортогональны

относительно весовой функции в интервале

Приведем несколько первых многочленов Лагерра:

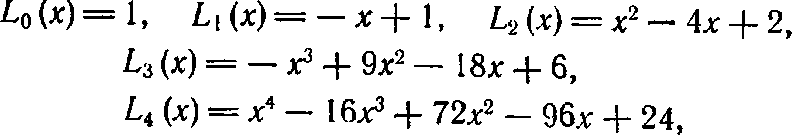
где функции заданы, а остальные получены по формуле (2.7.16).

Многочлены Эрмита

Для получения многочленов Эрмита используется рекуррент­ное соотношение

(2.7.18)

где Эти функции ортогональны относи-

тельно весовой функции причем интервал

ортогональности составляет это обстоятельство

делает использование таких функций чрезвычайно удобным, по­скольку освобождает нас от забот относительно диапазона из­менения переменных.

Приведем несколько первых многочленов Эрмита:

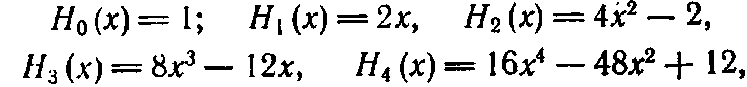
где функции заданы, а остальные определяются

по формуле (2.7.18).

2.4 Аппроксимация плотностей распределения функциями

Постановка задачи

Пусть — оценка плотности распределения при-

чем, как и раньше, под подразумевается .

Необходимо найти такую оценку, которая обеспечила бы минимиза­цию среднеквадратичной ошибки (интегрального квадратичного показателя качества), определяемой как

(4.6.47)

где — весовая функция.

Воспользуемся разложением оценки в ряд

где —коэффициенты, подлежащие определению, а —

множество заданных базисных функций.

Подстановка (4.6.48) в соотношение (4.6.47) дает

(4.6.49)

Требуется найти такие коэффициенты которые обеспечат

минимизацию интеграла вероятности ошибки R. Необходимое условие минимальности интеграла вероятности ошибки R за­ключается в том, что

( 4.6.50)

Взяв частную производную, получим

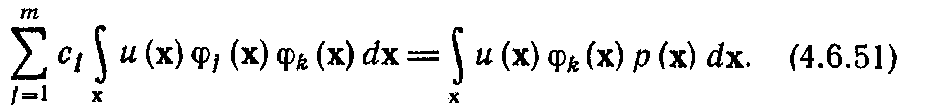
Взглянув на правую часть уравнения (4.6.51), нетрудно убе­диться в том, что она по определению равна математическому ожиданию функции . В соответствии с нашим предыдущим анализом математическое ожидание можно аппрокси­мировать выборочным средним, т. е.

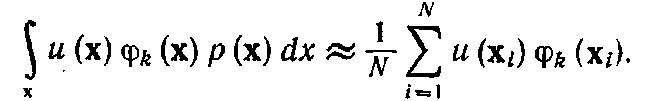(4.6.52)

Подстановка этой аппроксимирующей оценки в уравнение (4.6.51) дает

(4.6.53)

Если базисные функции выбраны таким образом, что

они ортогональны весовой функции , то из определения

ортогональности следует

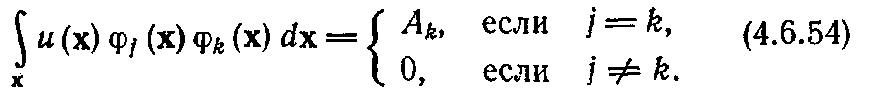
Подстановка (4.6.54) в уравнение (4.6.53) приводит к следую­щему соотношению, позволяющему вычислить искомые коэф­фициенты:

Если базисные функции ортонормированны, то

для всех Кроме того, поскольку члены не зависят от

и, следовательно, для всех коэффициентов одинаковы, то их можно исключить из аппроксимирующего выражения без вся­кого ущерба для классификационной мощности коэффициентов. В таком случае

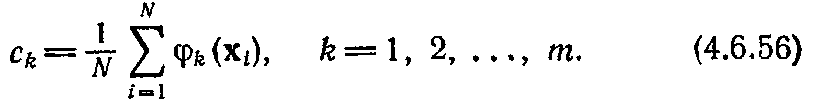
После того как коэффициенты определены, с помощью форму­лы (4.6.48) формируется оценка плотности распределения

Для того чтобы применение выражений (4.6.48) и (4.6.55) или (4.6.56) приводило к успеху, необходимо иметь в виду два существенных обстоятельства. Во-первых, следует полностью отдавать себе отчет в том, что качество аппроксимации с по­мощью выбранной системы базисных функций зависит от числа m членов разложения. Поскольку, по всей вероятности, вид плотности распределения нам не известен, оценить

качество аппроксимации при помощи непосредственного

сравнения невозможно. С другой стороны, так как оценка

отыскивается для того, чтобы построить байесовский классифи­катор, то заботиться следует только о качестве распознавания, доступном этому классификатору. Последнее можно установить непосредственно в эксперименте с обучающей выборкой. Если при некоторой оценке качество классификации оказывается неудовлетворительным, следует попробовать увеличить число базисных функций и посмотреть, приводит ли улучшение качества оценки к улучшению качества классификатора.

Эту процедуру можно продолжать вплоть до наступления «на­сыщения» (когда введение дополнительных членов не произво­дит никакого либо очень малый эффект) или до тех пор, пока число членов не начнет превосходить допустимую величину.

Вторым важным моментом является выбор базисных функ­ций. Так, например, если плотность распределения имеет синусоидальный характер, а для разложения оценки ис­пользован степенной ряд, то очевидно, что число членов будет значительно больше, чем при выборе синусоидальных базисных функций. Естественно, при отсутствии априорных сведений о характере плотности распределения базисные функции в первую очередь должны выбираться исходя из простоты реали­зации. Все, что можно было бы сказать об общих правилах выбора базисных функций, сводится к тому, что при выполне­нии условия линейной независимости и некоторых других не очень жестких ограничений на вид плотности распределения можно доказать сходимость при и . Отметим, что ортогональность является частным слу­чаем линейной независимости.

Пример.

Дана обучающая выборка (см. Рис.1)

Известно, что образы , а образы

Рис. 1

Требуется по обучающей выборке построить оценки плотностей распределения.

Плотности можно аппроксимировать, применив выражения вида:

Базисные функции считаются ортогональными в области определения образов. Поскольку наши образы , будем использовать многочлены Лежандра, так как областью их ортогональности является интервал .

В одномерном случае эти функции определяются следующим рекуррентным соотношением:

Первые члены функции P(x) имеют следующий вид:

и

Все эти функции ортогональны. Ортонормированные функции определяются следующим выражением:

В иллюстративных целях с ортогональными функциями мы будем обращаться так, как если бы они были ортонормированными.

Множество ортогональных функций для двумерного случая легко получить, формируя произвольные попарные комбинации одномерных функций.

Пусть m=4.

где x₁,x₂ – компоненты образа x.

Очевидно, что порядок формирования этих функций не единственный. Для получения любой функции можно использовать произвольную парную комбинацию функций одной переменной.

Теперь определим коэффициенты разложения . Используя допущение ортонормированности функций, эти коэффициенты можно вычислить по формуле:

Для класса :

N₁- число образов, входящих в класс ,

Для образов класса , применение данной процедуры дает

Аналогично, для образов класса получим:

Аппроксимация плотности распределения такова

Аппроксимация плотности распределения такова:

6