1.3 Общее решение задачи с помощью метода неопределенных множителей Лагранжа

Использование множителей Лагранжа позволяет построить функцию

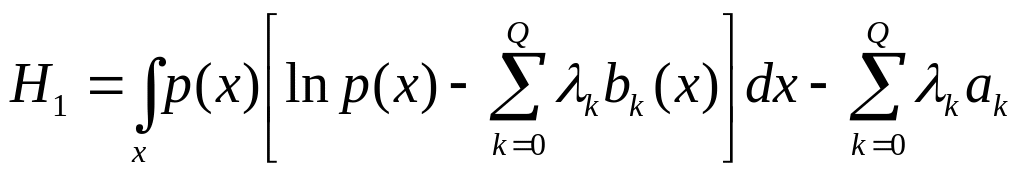, (2)

где a₀ = 1 и b₀(x) = 1 для всех образов x.

Взяв частные производные от функции H₁ по плотности рас­пределения p(x), имеем

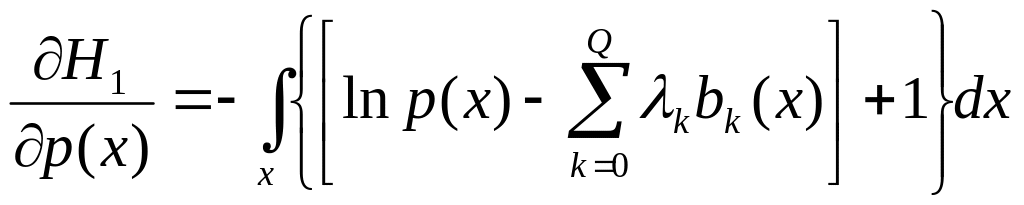(3)

Приравняв подынтегральное выражение нулю и выразив из этого уравнения p(x), получим

(4)

Здесь Q+1 параметров следует выбирать так, чтобы они соответствовали априорной информации об образах х, содержащейся в соотношениях (*) и (**).

Исходя из (4), легко показать, что, когда известно, что случайная величина отлична от нуля только в конечном интер­вале, следует выбирать равномерное распределение. Если случайная величина может принимать любое действительное значение, а единственными разумными характеристиками считаются математическое ожидание и дисперсия, то следует выбирать нормальное распределение. Выбрав плотность рас­пределения, необходимо заняться оценкой параметров выбран­ной функции. Проведенный анализ показывает, что при следо­вании энтропийной концепции выбор нормального распределения является вполне приемлемым допущением, если единствен­ными известными характеристиками образов х являются мате­матическое ожидание и дисперсия.

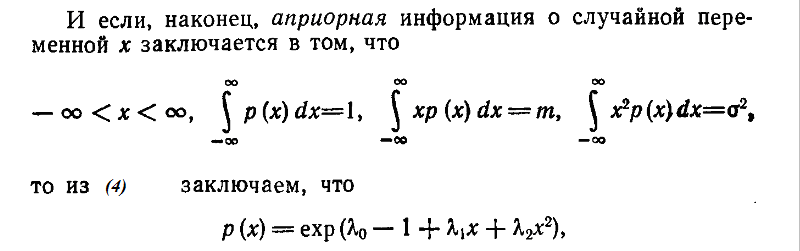
2. Способ оценки неизвестной плотности вероятности по апостериорным данным путем аппроксимации функциями.

2.1. Определения

Скалярное произведение двух функций f(x) и g(x) в интер­вале определяется как

Скалярное произведение функции f(x) на себя, называемое нормой функции f(x), вводится как

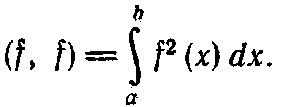(2.7.2)

Функция, норма которой равна единице, называется нормиро­ванной. Нормировка легко достигается делением функции на квадратный корень ее нормы.

Две функции f(x) и g(x) ортогональны относительно весовой функции и(х) в интервале [а, b], если

(2.7.3)

Система функций каждая пара которых

ортогональна в интервале [а,b], называется ортогональной си­стемой. Для этой системы функций имеют место обычные уcловия ортогональности:

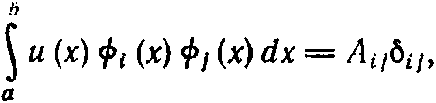(2.7.4)

где

(2.7.5)

коэффициент, зависящий от параметров i и j. Поскольку правая часть уравнения (2.7.4) всегда равна нулю, за исключе­нием случая коэффициент записывают просто в виде При для всех значений система функций называется ортонормированной системой, а соответствующие условия ортонормированности задаются следующим образом:

(2.7.6а)

Множество функций называется ли-

нейно независимым, если не существует коэффициентов не всех равных нулю и таких, что уравнение

(2.7.9)

справедливо для всех х. Все функции, образующие ортогональ­ную систему, линейно независимы.

И наконец, система функций называется полной, если любую кусочно-непрерывную функцию можно в среднем сколь угодно точно аппроксимировать с помощью линейной комбинации функ­ций, входящих в данную систему.

2.2. Построение функций многих переменных

Пусть нам задана полная система ортонормированных функ­ций одной переменной на интервале В таком случае полную систему ортонормированных функций двух переменных можно построить следующим образом:

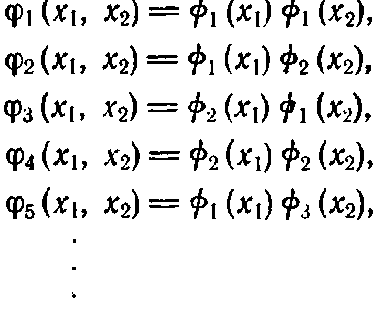(2.7.10)

Отметим, что использованное выше правило построения сводится просто к выбору пар функций из множества функций одной переменной и перемножению их после соответствующей подстановки переменных x₁,x₂.

Способ распространения описанной процедуры на общий случай п переменных очевиден. Здесь требуется только со­ставлять группы произведений из п функций одной переменной, подставляя соответственно переменные Если исходные функции ортонормированны в интервале то полученные в результате реализации этой процедуры функции п переменных ортонормированны на гиперкубе

В частности, множество функций п переменных при строится следующим образом:

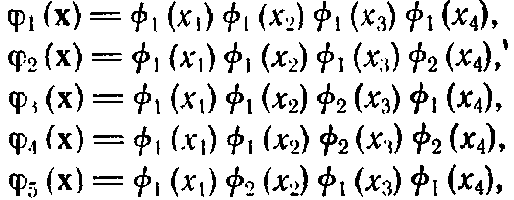(2.7.13)

где, как и выше,