
Правила обрання чисел [aij] та [bi]:
1. Якщо дробові числа aij або bi є додатними числами, то [aij] та [bi] є цілими додатними числами і дорівнюють цілій частині числа aij або bi. Наприклад:
![]()
2. Якщо дрібне число aij або bi є від’ємним числом, то [aij] та [bi] є від’ємним цілим числом, яке за абсолютним значенням на “1” більше за абсолютне значення цілої частини числа aij або bi. Наприклад:
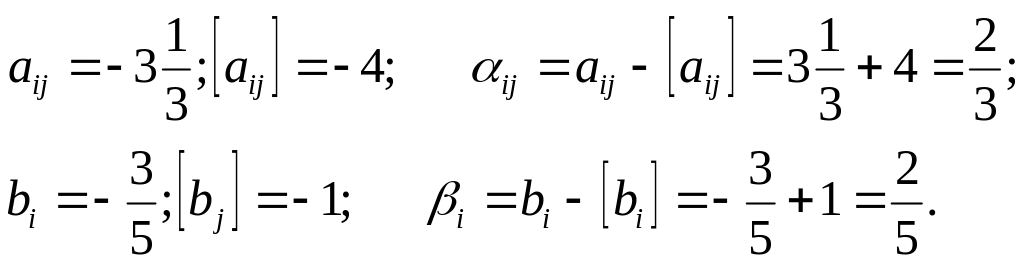
Якщо aij або bi є цілими числами, то αij =0, βi =0.
3.
Додаткова нерівність (3) має лише додатні
коефіцієнти. Вона множенням на «-1»
спочатку приводиться до вигляду, який
повинна мати нерівність у симплекс-методі
згідно зі стандартною формою (![]() )
)
![]() ,
а потім за допомогою додаткової змінної
,
а потім за допомогою додаткової змінної
![]() перетворюється у рівняння
перетворюється у рівняння
![]() ,
яке додається до оптимального опорного
плану – системи (2) і разом із ним створює
псевдоплан (має одне від’ємне значення
,
яке додається до оптимального опорного
плану – системи (2) і разом із ним створює
псевдоплан (має одне від’ємне значення
![]() ).
).
Якщо
в новому оптимальному опорному плані
існують базисні змінні
![]() ,
які мають дробові значення, то знов
додають одне додаткове обмеження, і
процес розрахунків повторюється до
отримання цілочисельних значень базисних
змінних.
,
які мають дробові значення, то знов
додають одне додаткове обмеження, і
процес розрахунків повторюється до
отримання цілочисельних значень базисних
змінних.
Ознакою
відсутності розв’язку задачі є наявність
у таблиці хоча б одного рядка з цілими
величинами aij
та
вільним дробовим членом bi,
що вказує на відсутність розв’язку в
цілих числах (наприклад,
![]() )
.
)
.
Часткові цілочислові задачі (в них вимоги щодо цілочисельності ставляться лише до окремих змінних) розв’язуються так само, як попередні, за рахунок введення додаткового обмеження
![]() ,
,
де ![]() -
визначається з відношень:
-
визначається з відношень:
для нецілочислових значень змінних
 :
:
![]() ;
;
2) для цілочисельних значень змінних :
![]() .
.
Приклад 3. Розв’язати лінійну задачу цілочислового програмування.
Знайти
![]() ,
,
при обмеженнях за умов:
![]()
Розв’язання:
і |
Базис |
Сбаз |
Опор-ний план В |
1 |
-1 |
-3 |
0 |
0 |
0 |
А1 |
А2 |
А3 |
А4 |
А5 |
А6 |
||||
1 |
А3 |
-3 |
4 |
0 |
0 |
1 |
2 |
1 |
0 |
2 |
А2 |
-1 |
11/3 |
0 |
1 |
0 |
-1/3 |
1/3 |
2/3 |
3 |
А1 |
1 |
1/3 |
1 |
0 |
0 |
-2/3 |
-1/3 |
1/3 |
|
|
-46/3 |
0 |
0 |
0 |
-19/3 |
-11/3 |
-1/3 |
|
Нецілими є такі компоненти опорного плану:
![]() .
. 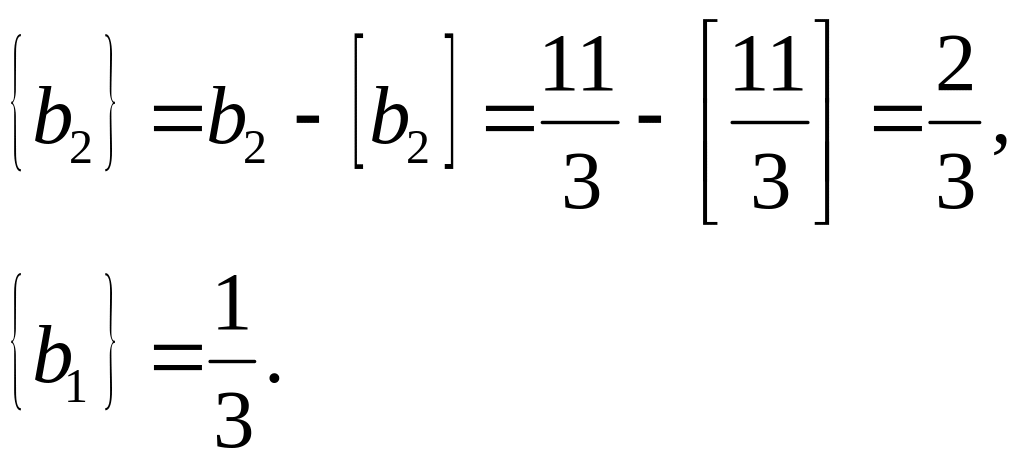
![]() : додаткове обмеження (1) буде сформовано
для і=2
(
: додаткове обмеження (1) буде сформовано
для і=2
(![]() - це обмеження можна представити у
вигляді:
- це обмеження можна представити у
вигляді:
![]() .
.
Зведемо його до канонічного виду з виділенням базисної змінної:
![]() .
.
і |
Базис |
Сбаз |
Опор-ний план В |
1 |
-1 |
-3 |
0 |
0 |
0 |
0 |
М |
θ |
А1 |
А2 |
А3 |
А4 |
А5 |
А6 |
А7 |
А8 |
|||||
1 |
А3 |
-3 |
4 |
0 |
0 |
1 |
2 |
1 |
0 |
0 |
0 |
|
2 |
А2 |
-1 |
11/3 |
0 |
1 |
0 |
-1/3 |
1/3 |
2/3 |
0 |
0 |
11/2 |
3 |
А1 |
1 |
1/3 |
1 |
0 |
0 |
-2/3 |
-1/3 |
1/3 |
0 |
0 |
1 |
4 |
А8 |
М |
2/3 |
0 |
0 |
0 |
2/3 |
1/3 |
2/3 |
-1 |
1 |
1 |
|
|
-46/3 |
0 |
0 |
0 |
-19/3 |
-11/3 |
-1/3 |
0 |
0 |
|
|
|
+2/3М |
0 |
0 |
0 |
+2/3М |
+1/3М |
+2/3М |
-М |
0 |
|||
і |
Базис |
Сбаз |
Опор-ний план В |
1 |
-1 |
-3 |
0 |
0 |
0 |
0 |
М |
А1 |
А2 |
А3 |
А4 |
А5 |
А6 |
А7 |
А8 |
||||
1 |
А3 |
-3 |
4 |
0 |
0 |
1 |
2 |
1 |
0 |
0 |
0 |
2 |
А2 |
-1 |
3 |
0 |
1 |
0 |
-1 |
0 |
0 |
1 |
-1 |
3 |
А1 |
1 |
0 |
1 |
0 |
0 |
-1 |
-1/2 |
0 |
1/2 |
-1/2 |
4 |
А6 |
0 |
1 |
0 |
0 |
0 |
1 |
1/2 |
1 |
-3/2 |
3/2 |
|
|
-15 |
0 |
0 |
0 |
-6 |
-7/2 |
0 |
-1/2 |
1/2 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
-М |
||
