
- •Написать канонические и параметрические уравнения прямой, заданной как линия пересечения двух плоскостей:
- •Написать канонические и параметрические уравнения прямой, заданной как линия пересечения двух плоскостей:
- •Найти проекцию точки м(3; 1; –1) на плоскость
- •Найти угол между прямой и плоскостью .
- •Составить уравнение плоскости, проходящей через прямые и
- •Написать канонические и параметрические уравнения прямой, заданной как линия пересечения двух плоскостей:
- •Написать канонические и параметрические уравнения прямой, заданной как линия пересечения двух плоскостей:
Вариант 1.
Найти расстояние от точки М(3; 2; –1) до плоскости, проходящей через три заданные точки А(1; –1; 4), В(–3; 0; 5), С(2; –2; 4).
Найти угол между плоскостями
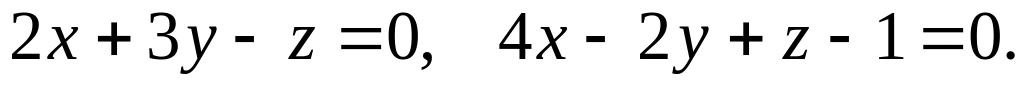
Написать канонические и параметрические уравнения прямой, заданной как линия пересечения двух плоскостей:
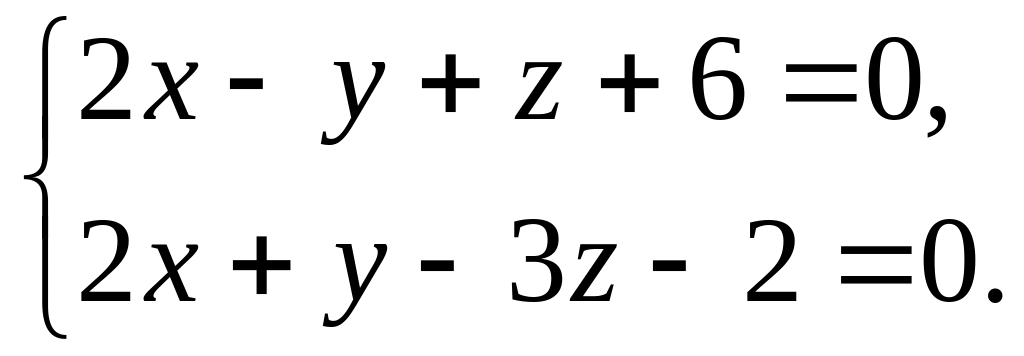
Найти проекцию точки М(3; 1; –1) на плоскость
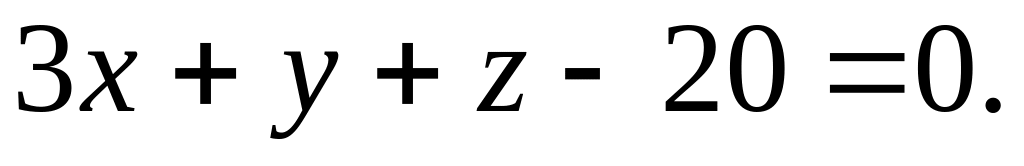
Вариант 2.
Найти расстояние от точки М(–1; 1; –2) до плоскости, проходящей через три заданные точки А(1; –1; 1), В(–2; 1; 3), С(4; –5; –2).
Найти угол между плоскостями
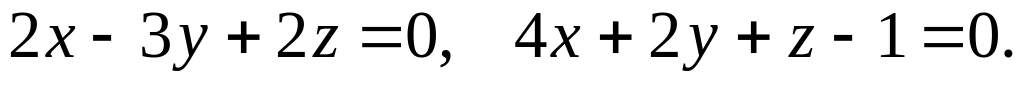
Написать канонические и параметрические уравнения прямой, заданной как линия пересечения двух плоскостей:
Найти проекцию точки М(3; 1; –1) на плоскость
Вариант 3.
Найти расстояние от точки М(2; –2; –1) до плоскости, проходящей через три заданные точки А(1; –1; 5), В(–2; 1; 5), С(1; –2; 4).
Найти угол между плоскостями
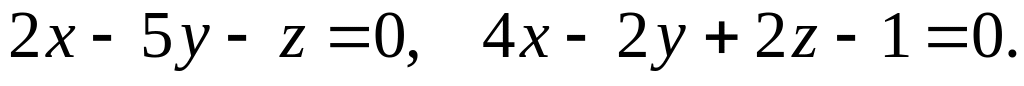
Написать канонические и параметрические уравнения прямой, заданной как линия пересечения двух плоскостей:
Найти проекцию точки м(3; 1; –1) на плоскость
Вариант № 4
1. Написать уравнение плоскости, проходящей
через ось ОХ и точку
![]() .
.
Написать уравнение прямой, проходящей через начало координат и точку
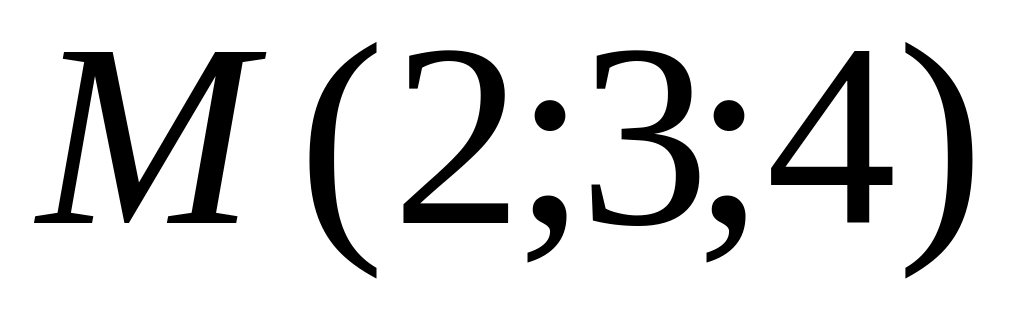 .
.Найти угол между прямой
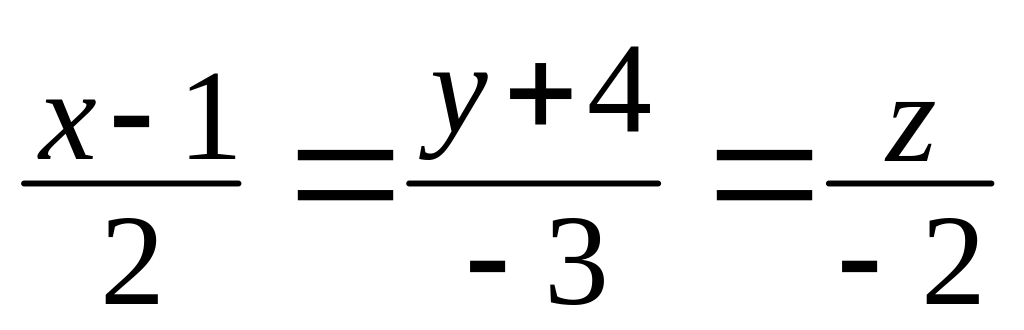 и плоскостью
и плоскостью
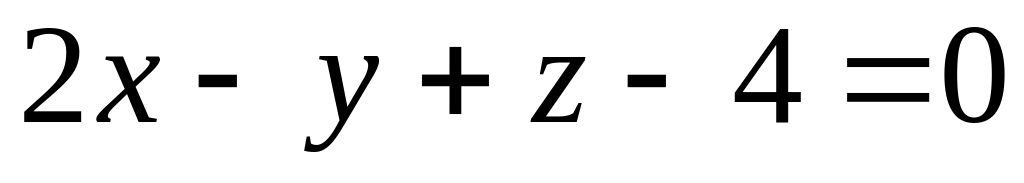 .
.Найти точку
 ,
симметричную точке
,
симметричную точке
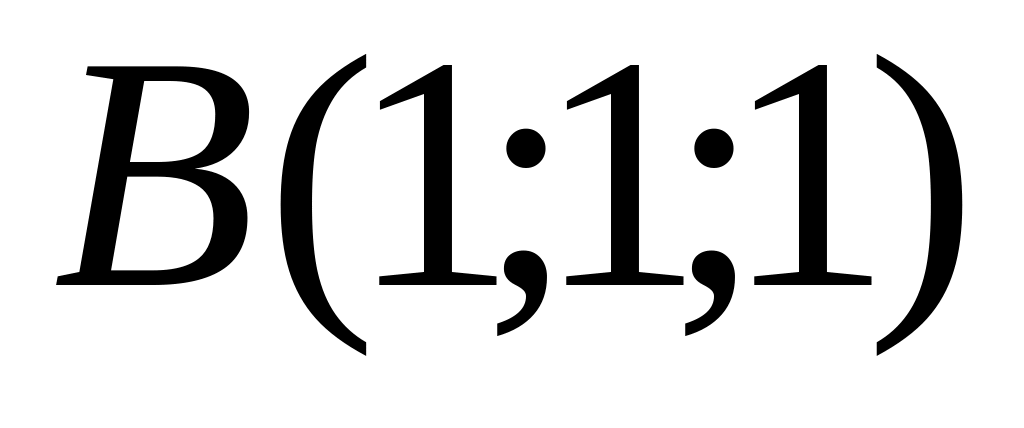 относительно прямой
относительно прямой
 .
.
Вариант № 5
1. Через точку
![]() провести плоскость перпендикулярно
прямой
провести плоскость перпендикулярно
прямой
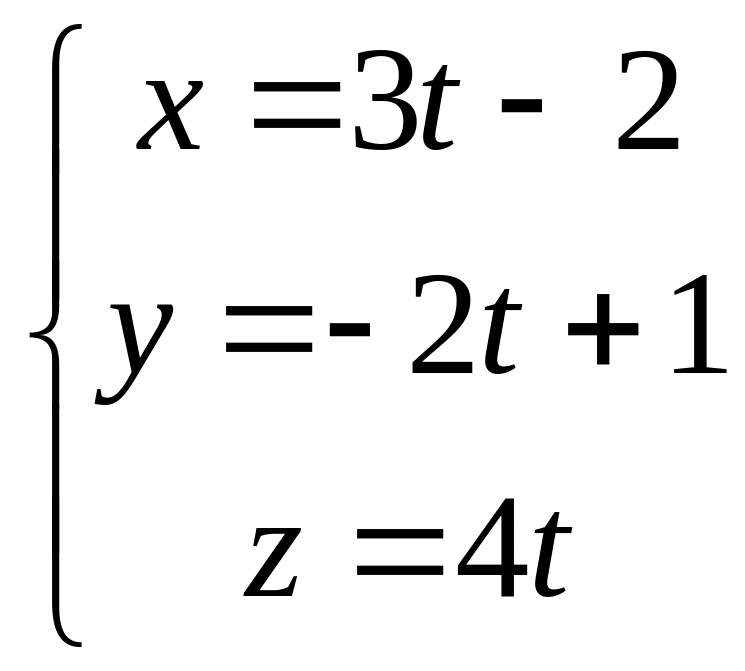 .
.
Написать уравнение прямой, проходящей через точку
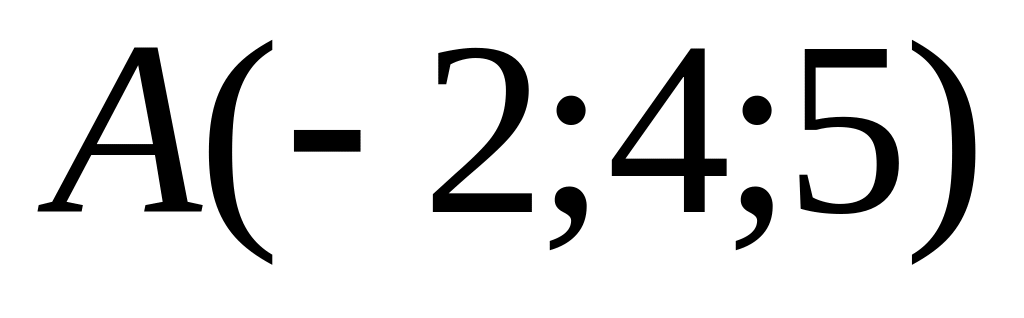 параллельно
оси ОZ.
параллельно
оси ОZ.Найти угол между прямыми
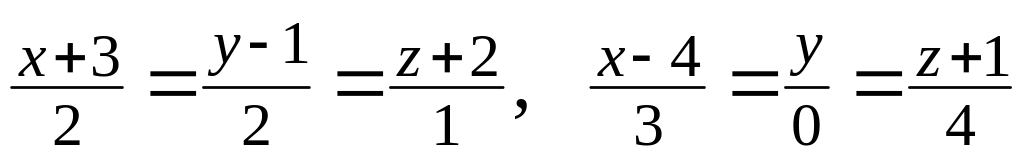 .
.Точки
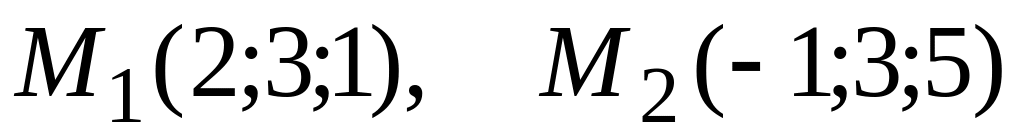 лежат на прямой. Составить уравнение
прямой.
лежат на прямой. Составить уравнение
прямой.
Вариант № 6
1. Написать уравнение плоскости, проходящей
через точку
![]() ,
параллельно плоскости
,
параллельно плоскости
![]() .
.
Написать канонические уравнения перпендикуляра, опущенного из начала координат на плоскость
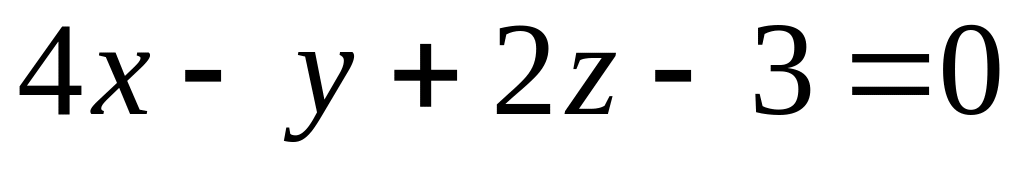 .
.Найти угол между прямой и плоскостью .
Составить уравнение плоскости, которая проходит через начало координат, перпендикулярно плоскостям
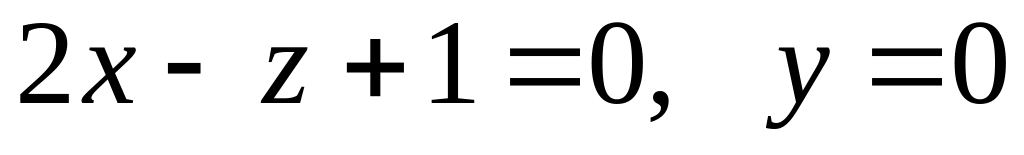 .
.
Вариант № 7
Написать уравнение плоскости, проходящей через прямые
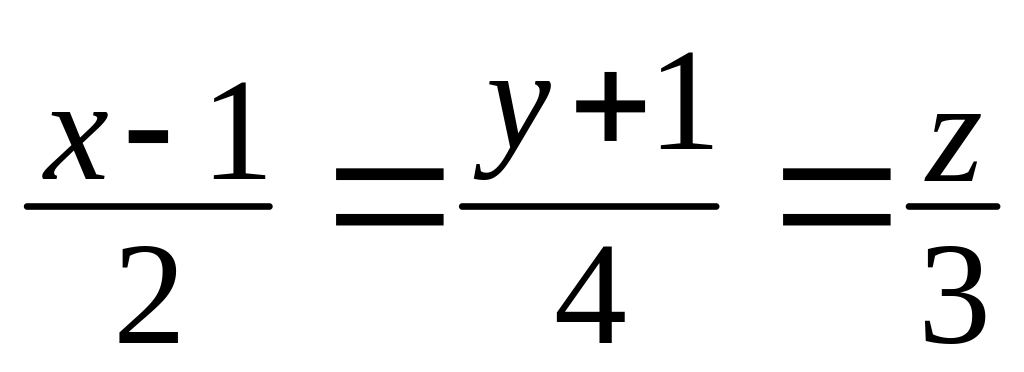 ,
,
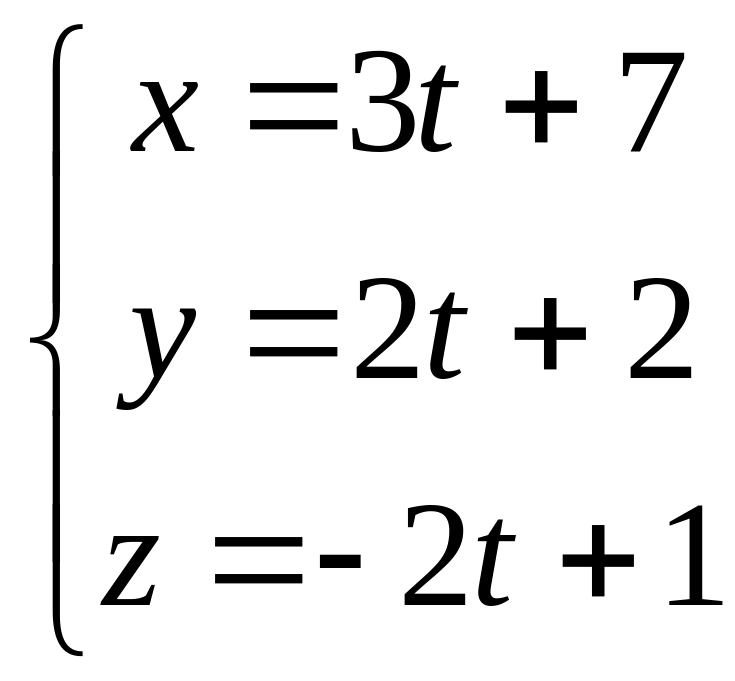 .
.Определить взаимное расположение прямой
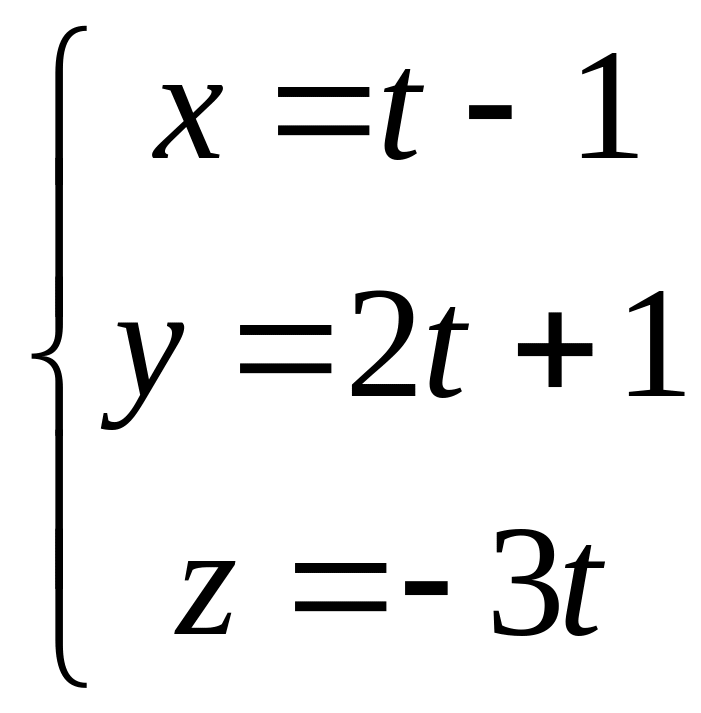 и плоскости
и плоскости
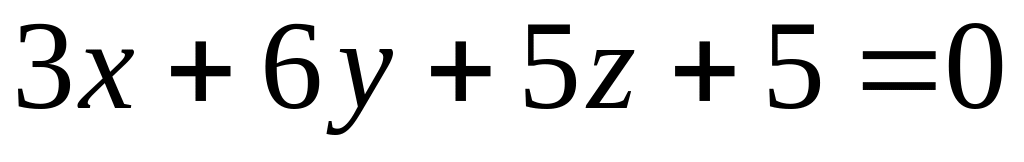 .
.Составить уравнение плоскости, которая проходит через две точки
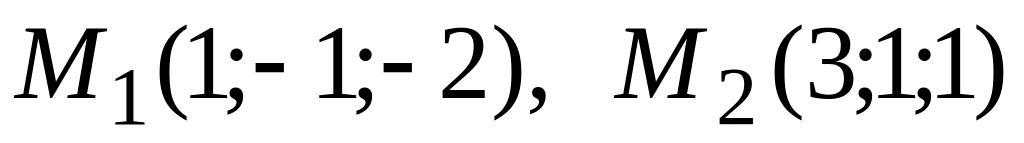 перпендикулярно к плоскости
перпендикулярно к плоскости
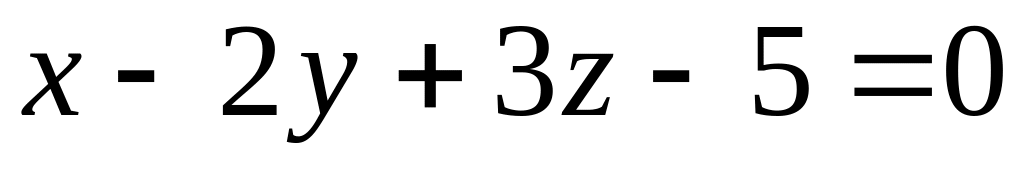 .
.Составить уравнение плоскости, проходящей через прямые
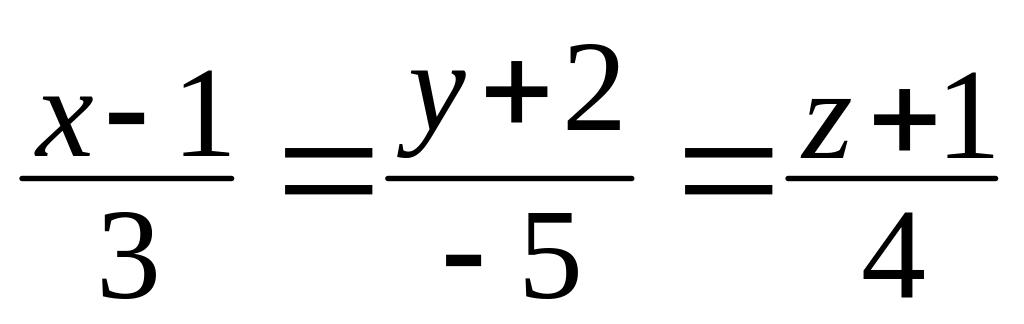 и
и
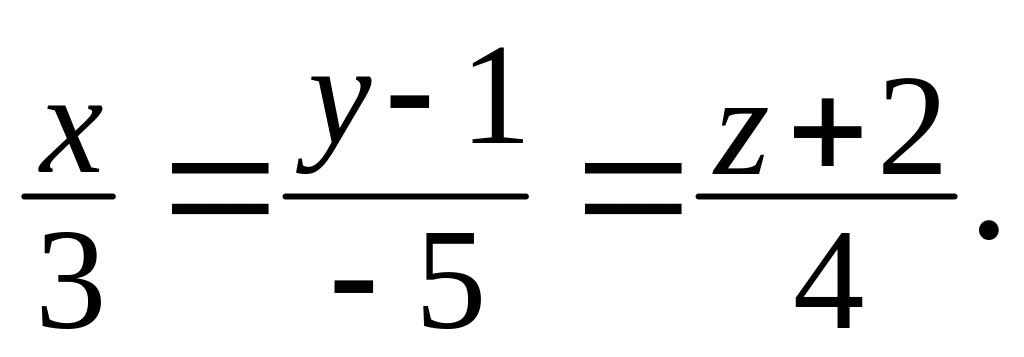
Вариант № 8
Написать уравнения прямой, проходящей через точку
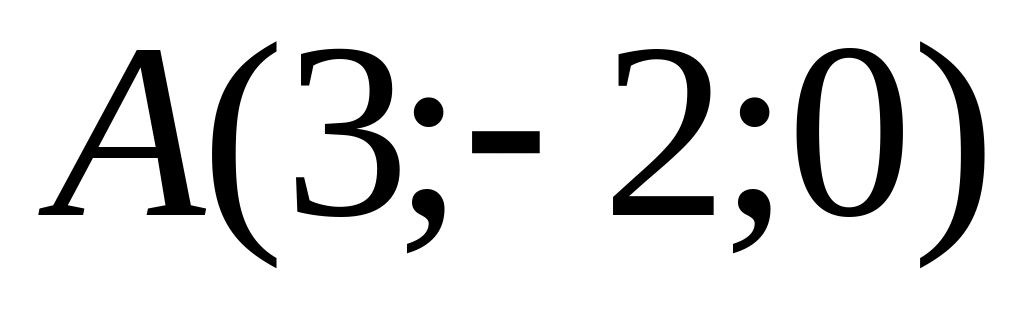 перпендикулярно к прямой
перпендикулярно к прямой
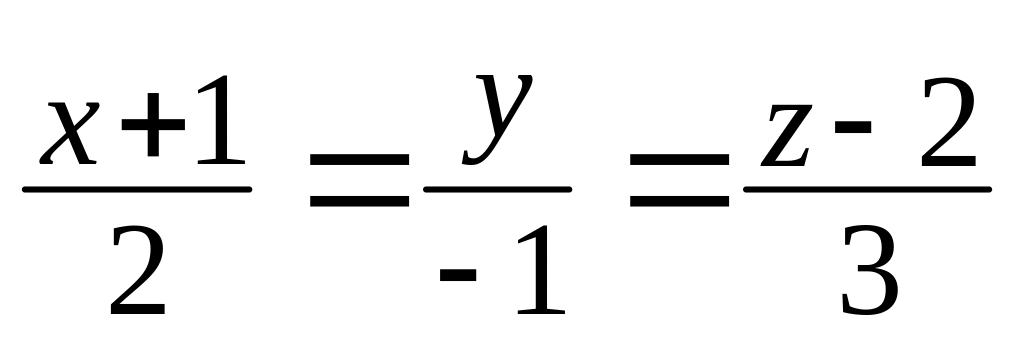 и расположенной в плоскости XOY.
и расположенной в плоскости XOY.Написать уравнение плоскости, проходящей через прямую
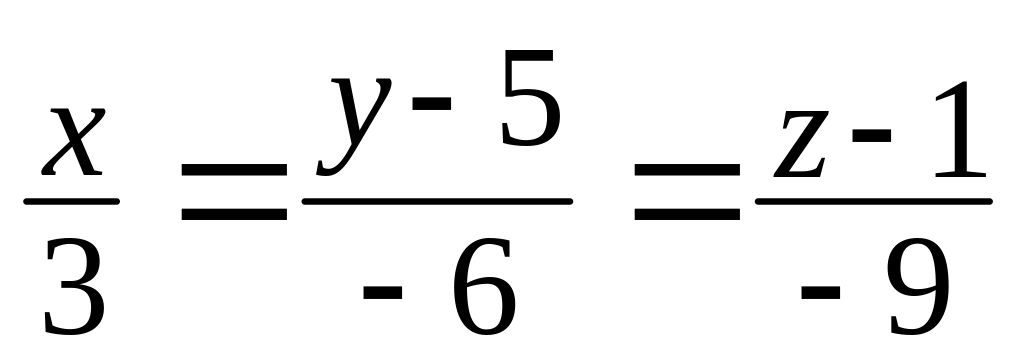 ,
перпендикулярно плоскости
,
перпендикулярно плоскости
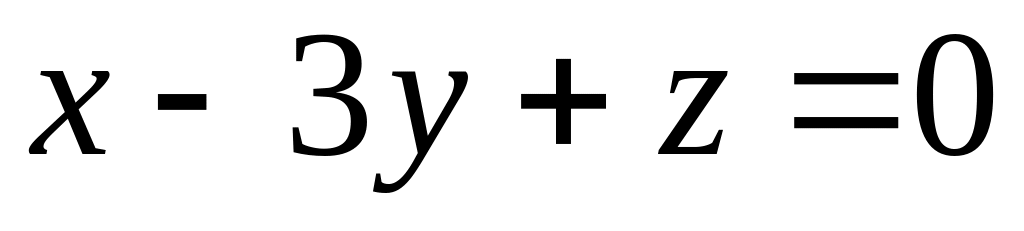 .
.Доказать, что три плоскости
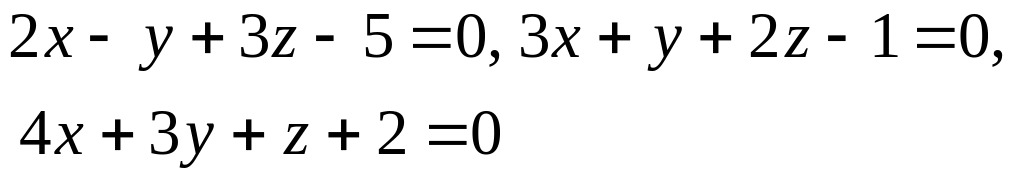 пересекаются
по трем различным параллельным прямым.
пересекаются
по трем различным параллельным прямым.Составить уравнение плоскости, проходящей через точку С(2; –1; 3) и параллельной прямым
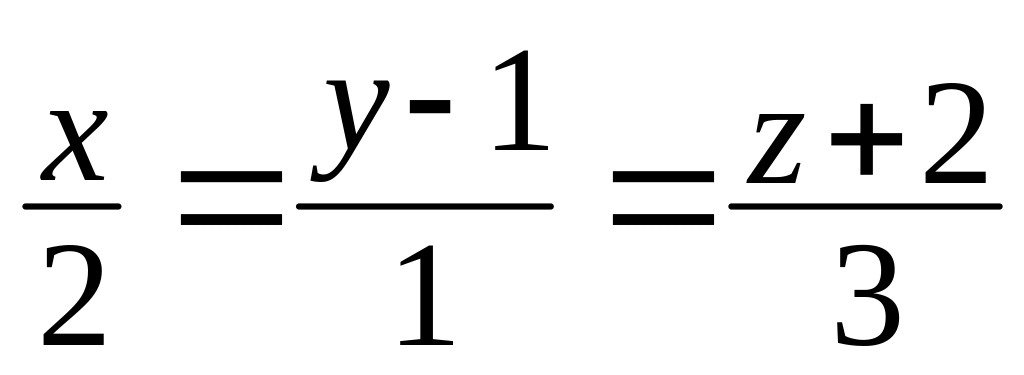 и
и
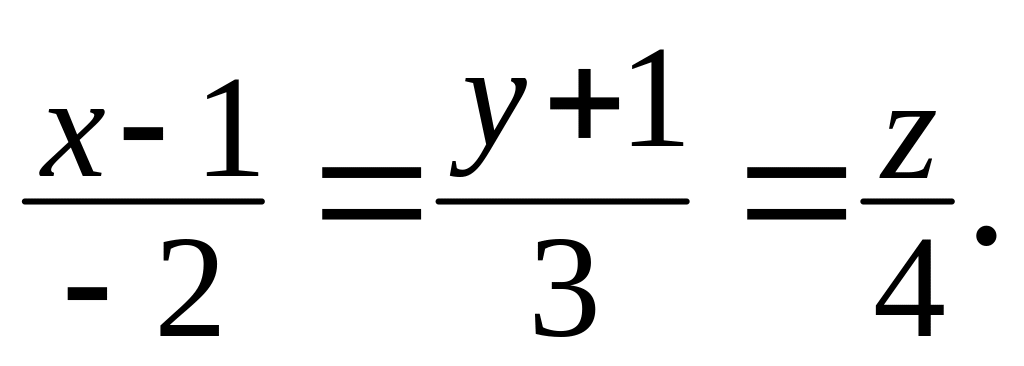
Вариант № 9
Даны точки
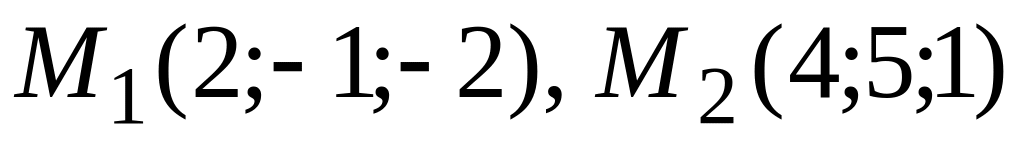 .
Составить уравнение плоскости, проходящей
через точку
.
Составить уравнение плоскости, проходящей
через точку
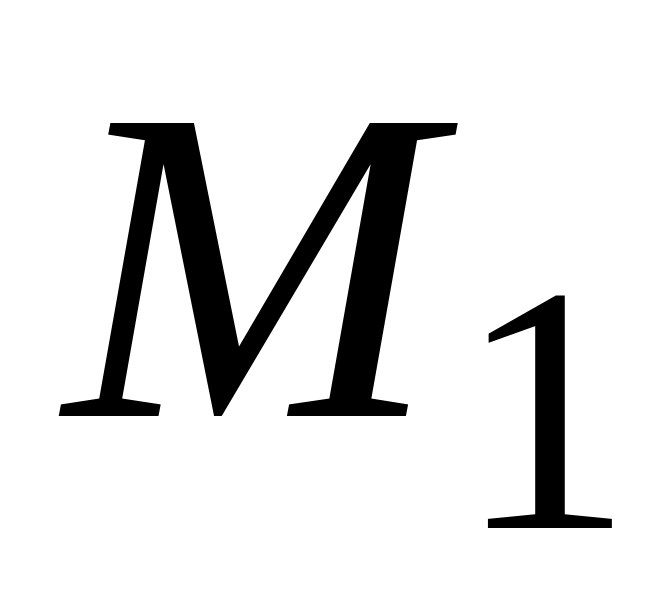 ,
перпендикулярно вектору
,
перпендикулярно вектору
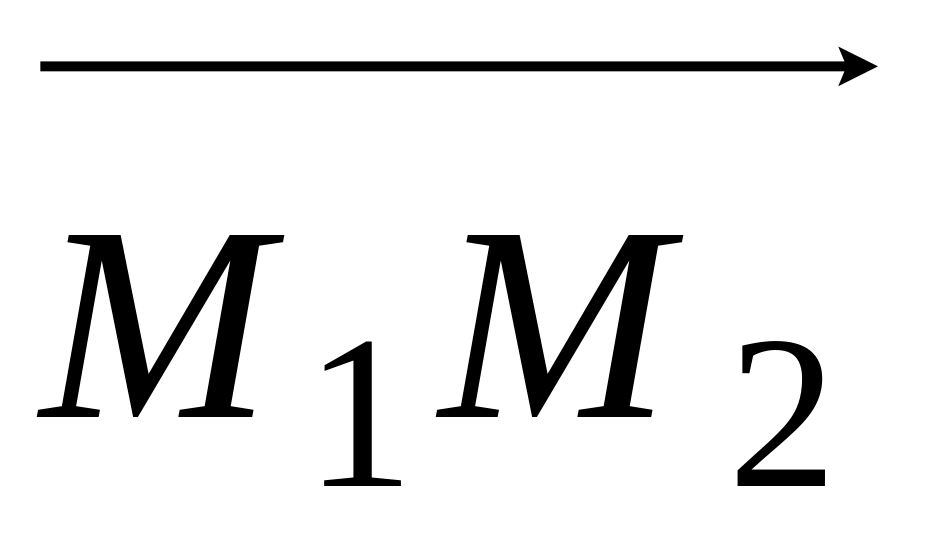 .
.Составить уравнения прямой, проходящей через точку
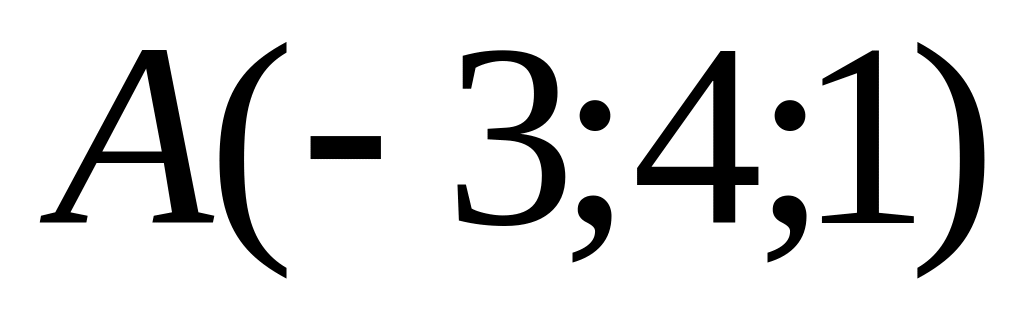 ,
параллельно прямой
,
параллельно прямой
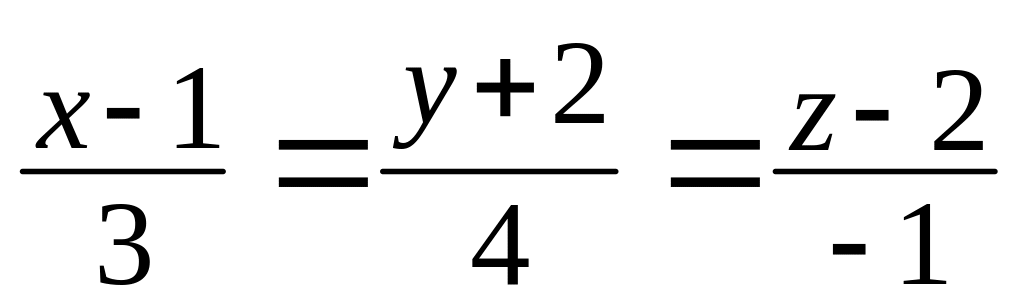 .
.Вычислить площадь треугольника, который отсекает плоскость
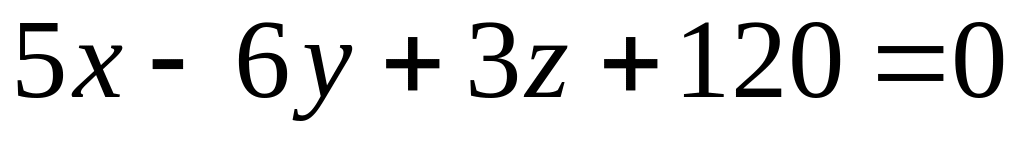 от координатного угла
от координатного угла
 .
.Составить уравнение плоскости, проходящей через прямые и
Вариант № 10
Написать уравнение плоскости, проходящей через прямую
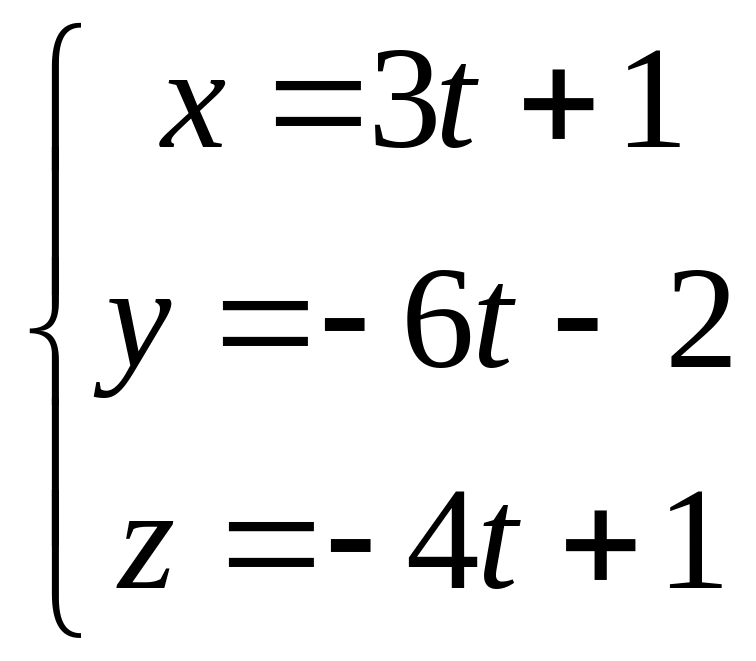 ,
перпендикулярно вектору
,
перпендикулярно вектору
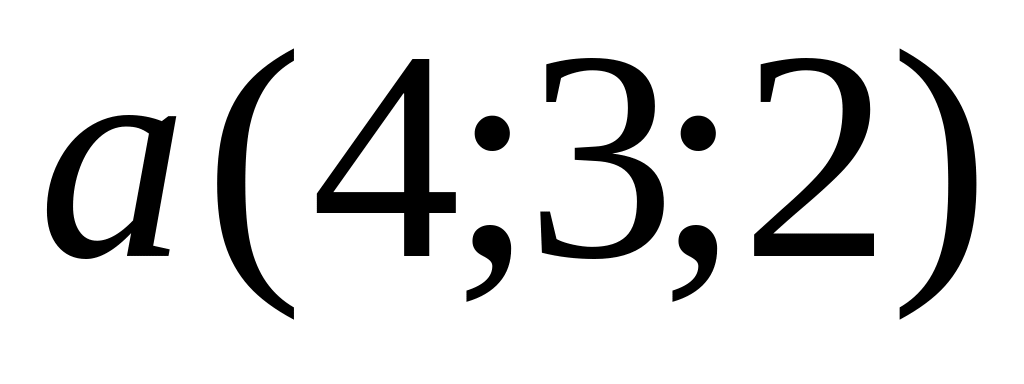 .
.Написать канонические уравнения прямой, проходящей через точку
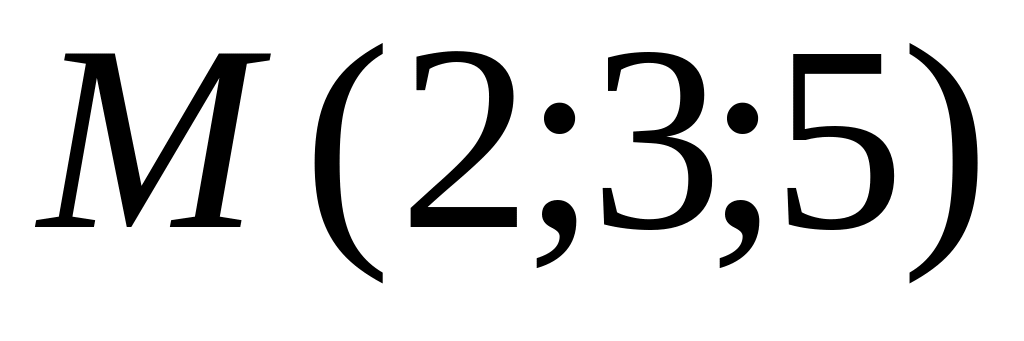 параллельно оси ОХ.
параллельно оси ОХ.Плоскость проходит через точку
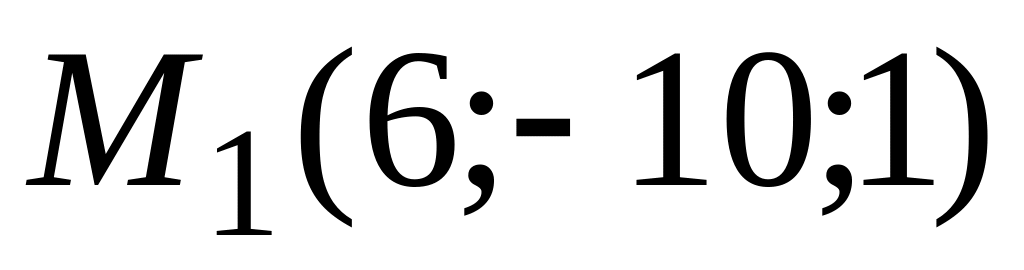 и осекает на оси абсцисс отрезок
и осекает на оси абсцисс отрезок
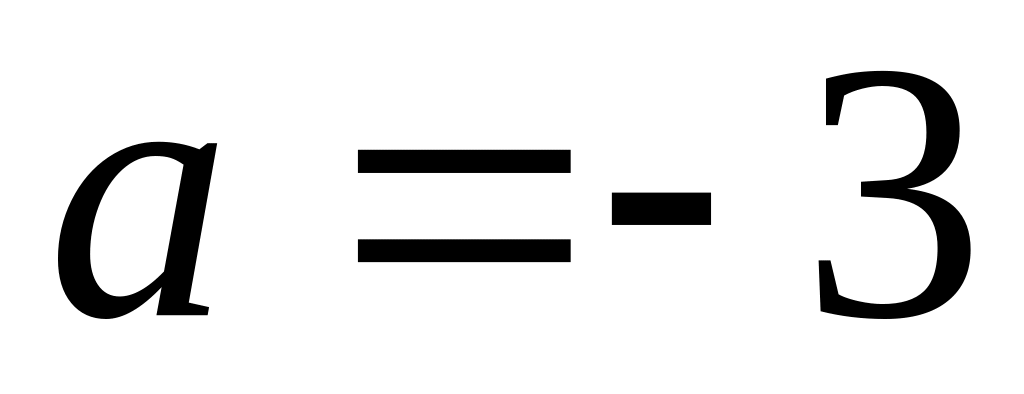 и на оси аппликат отрезок
и на оси аппликат отрезок
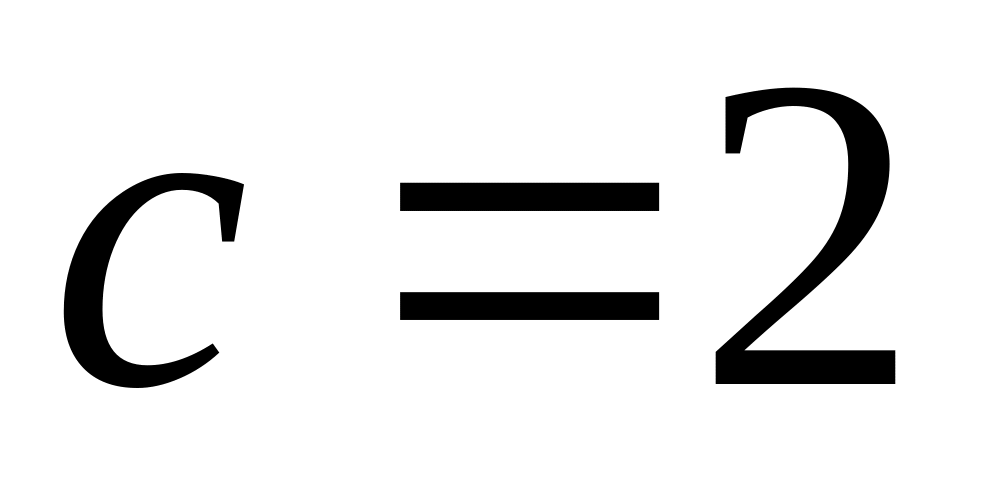 .
Составить уравнение плоскости.
.
Составить уравнение плоскости.Написать канонические и параметрические уравнения прямой, заданной как линия пересечения двух плоскостей:
Вариант № 11
Составить уравнение плоскости, проходящей через начало координат, параллельно плоскости
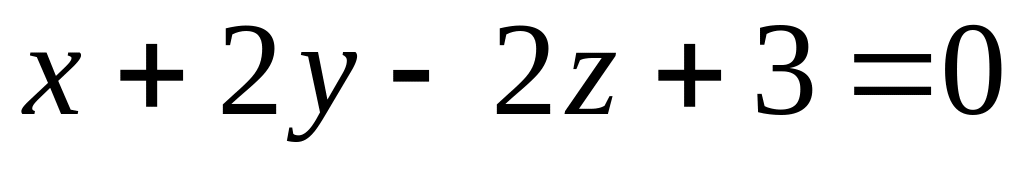 .
.Написать уравнение перпендикуляра, опущенного из точки
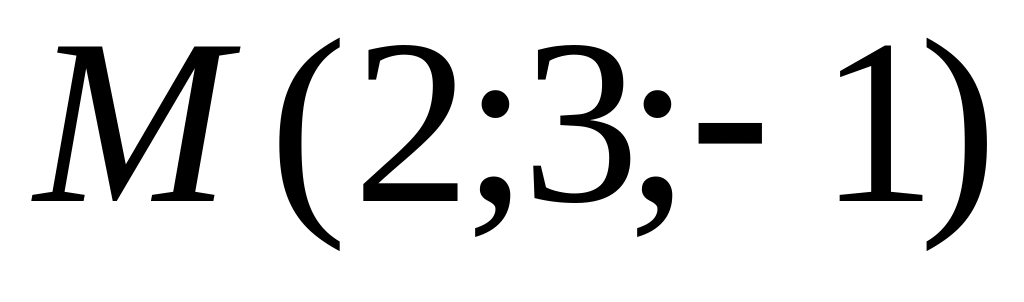 на плоскость
на плоскость
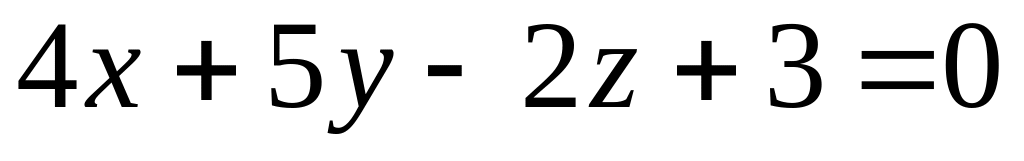 .
.Составить уравнение плоскости, которая проходит через точку
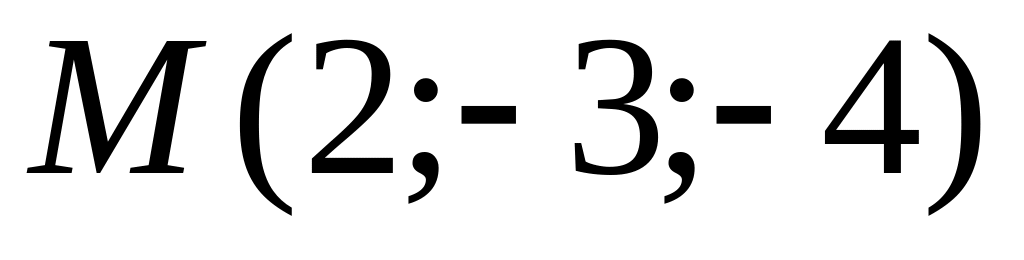 и
отсекает на осях координат отличные
от нуля отрезки одинаковой длины.
и
отсекает на осях координат отличные
от нуля отрезки одинаковой длины.Составить уравнение плоскости, проходящей через точку
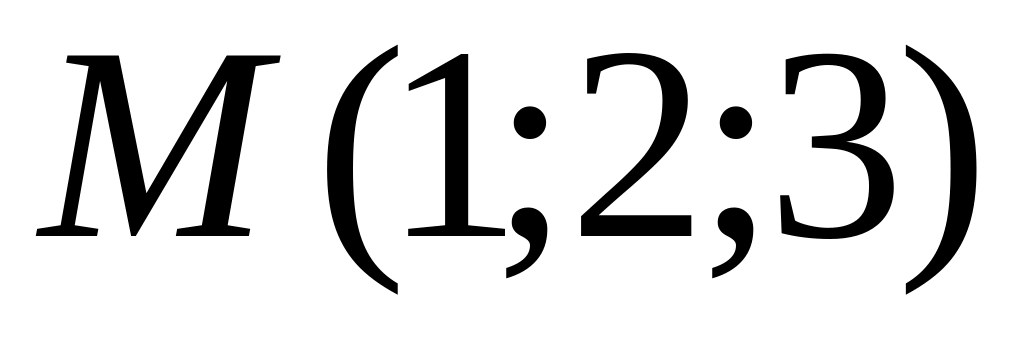 параллельно
прямым
параллельно
прямым
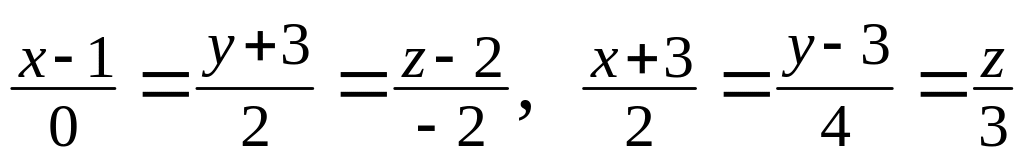 .
.
Вариант № 12
