
С помощью матрицы алгебраических дополнений
![]()
![]() —
транспонированная матрица
алгебраических дополнений;
—
транспонированная матрица
алгебраических дополнений;
Полученная матрица A−1 и будет обратной. Сложность алгоритма зависит от сложности алгоритма расчета определителя Odet и равна O(n²)·Odet.
Иначе говоря, обратная матрица равна единице, делённой на определитель исходной матрицы и умноженной натранспонированную матрицу алгебраических дополнений элементов исходной матрицы.
Использование lu/lup-разложения
Матричное
уравнение ![]() для
обратной матрицы
для
обратной матрицы ![]() можно
рассматривать как совокупность
можно
рассматривать как совокупность ![]() систем
вида
.
Обозначим
систем
вида
.
Обозначим ![]() -ый
столбец матрицы
через
-ый
столбец матрицы
через ![]() ;
тогда
;
тогда ![]() ,
, ![]() ,поскольку
-м
столбцом матрицы
,поскольку
-м
столбцом матрицы ![]() является
единичный вектор
является
единичный вектор ![]() .
другими словами, нахождение обратной
матрицы сводится к решению n уравнений
с одной матрицей и разными правыми
частями. После выполнения LUP-разложения
(время O(n³)) на решение каждого из n
уравнений нужно время O(n²), так что и эта
часть работы требует времени O(n³)[1].
.
другими словами, нахождение обратной
матрицы сводится к решению n уравнений
с одной матрицей и разными правыми
частями. После выполнения LUP-разложения
(время O(n³)) на решение каждого из n
уравнений нужно время O(n²), так что и эта
часть работы требует времени O(n³)[1].
Если
матрица A невырождена, то для неё можно
рассчитать LUP-разложение ![]() .
Пусть
.
Пусть ![]() ,
, ![]() .
Тогда из свойств обратной матрицы можно
записать:
.
Тогда из свойств обратной матрицы можно
записать: ![]() .
Если умножить это равенство на U и L то
можно получить два равенства вида
.
Если умножить это равенство на U и L то
можно получить два равенства вида ![]() и
и ![]() .
Первое из этих равенств представляет
собой систему из n² линейных уравнений
для
.
Первое из этих равенств представляет
собой систему из n² линейных уравнений
для ![]() из
которых известны правые части (из свойств
треугольных матриц). Второе представляет
также систему из n² линейных уравнений
для
из
которых известны правые части (из свойств
треугольных матриц). Второе представляет
также систему из n² линейных уравнений
для ![]() из
которых известны правые части (также
из свойств треугольных матриц). Вместе
они представляют собой систему из n²
равенств. С помощью этих равенств можно
реккурентно определить все n² элементов
матрицы D. Тогда из равенства (PA)−1 =
A−1P−1 =
B−1 =
D. получаем равенство
из
которых известны правые части (также
из свойств треугольных матриц). Вместе
они представляют собой систему из n²
равенств. С помощью этих равенств можно
реккурентно определить все n² элементов
матрицы D. Тогда из равенства (PA)−1 =
A−1P−1 =
B−1 =
D. получаем равенство ![]() .
.
В случае использования LU-разложения не требуется перестановки столбцов матрицы D но решение может разойтись даже если матрица A невырождена.
Сложность алгоритма — O(n³).
Итерационные методы
Методы Шульца
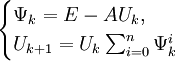
Оценка погрешности
Выбор начального приближения
Проблема
выбора начального приближения ![]() в
рассматриваемых здесь процессах
итерационного обращения матриц не
позволяет относиться к ним как к
самостоятельным универсальным методам,
конкурирующими с прямыми методами
обращения, основанными, например, на
LU-разложении матриц. Имеются некоторые
рекомендации по выбору
,
обеспечивающие выполнение
условия
в
рассматриваемых здесь процессах
итерационного обращения матриц не
позволяет относиться к ним как к
самостоятельным универсальным методам,
конкурирующими с прямыми методами
обращения, основанными, например, на
LU-разложении матриц. Имеются некоторые
рекомендации по выбору
,
обеспечивающие выполнение
условия ![]() (спектральный
радиус матрицы меньше единицы), являющегося
необходимым и достаточным для сходимости
процесса. Однако при этом, во-первых,
требуется знать сверху оценку спектра
обращаемой матрицы A либо матрицы
(спектральный
радиус матрицы меньше единицы), являющегося
необходимым и достаточным для сходимости
процесса. Однако при этом, во-первых,
требуется знать сверху оценку спектра
обращаемой матрицы A либо матрицы ![]() (а
именно, если A — симметричная
положительно определённая матрица и
(а
именно, если A — симметричная
положительно определённая матрица и ![]() ,
то можно взять
,
то можно взять ![]() ,
где
,
где 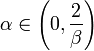 ;
если же A — произвольная невырожденная
матрица и
;
если же A — произвольная невырожденная
матрица и ![]() ,
то полагают
,
то полагают ![]() ,
где также
;
можно конечно упростить ситуацию и,
воспользовавшись тем, что
,
где также
;
можно конечно упростить ситуацию и,
воспользовавшись тем, что ![]() ,
положить
,
положить ![]() ).
Во-вторых, при таком задании начальной
матрицы нет гарантии, что
).
Во-вторых, при таком задании начальной
матрицы нет гарантии, что ![]() будет
малой (возможно, даже окажется
будет
малой (возможно, даже окажется ![]() ),
и высокий порядок скорости сходимости
обнаружится далеко не сразу.
),
и высокий порядок скорости сходимости
обнаружится далеко не сразу.
Примеры
Матрица 2х2
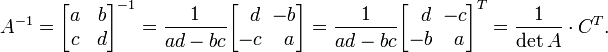
Обращение
матрицы 2х2 возможно только при условии,
что ![]() .
.
Транспонирование.
Транспонированная
матрица — матрица ![]() ,
полученная из исходной матрицы
заменой
строк на столбцы.
,
полученная из исходной матрицы
заменой
строк на столбцы.
Пример:
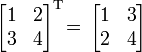 и
и 
Системы линейных уравнений
Решение
систем линейных уравнений методом
Крамера.
Пусть
нам требуется решить систему линейных
алгебраических уравнений
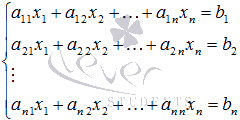 в
которой число уравнений равно числу
неизвестных переменных и определитель
основной матрицы системы отличен от
нуля, то есть,
в
которой число уравнений равно числу
неизвестных переменных и определитель
основной матрицы системы отличен от
нуля, то есть, ![]() .
Пусть
.
Пусть ![]() -
определитель основной матрицы системы,
а
-
определитель основной матрицы системы,
а ![]() -
определители матриц, которые получаются
из А заменой 1-ого,
2-ого, …, n-ого столбца
соответственно на столбец свободных
членов:
-
определители матриц, которые получаются
из А заменой 1-ого,
2-ого, …, n-ого столбца
соответственно на столбец свободных
членов:
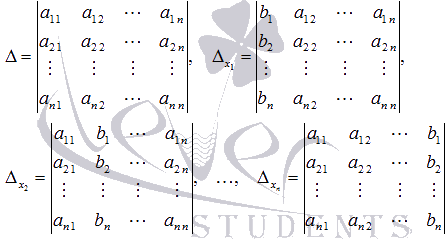 При
таких обозначениях неизвестные переменные
вычисляются по формулам метода Крамера
как
При
таких обозначениях неизвестные переменные
вычисляются по формулам метода Крамера
как 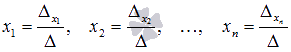 .
Так находится решение системы линейных
алгебраических уравнений методом
Крамера.
Пример.
Решите
систему линейных уравнений методом
Крамера
.
Так находится решение системы линейных
алгебраических уравнений методом
Крамера.
Пример.
Решите
систему линейных уравнений методом
Крамера 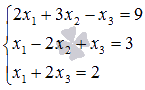 .
Решение.
Основная
матрица системы имеет вид
.
Решение.
Основная
матрица системы имеет вид 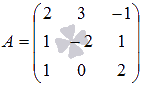 .
Вычислим ее определитель (при необходимости
смотрите статью определитель
матрицы: определение, методы вычисления,
примеры, решения):
.
Вычислим ее определитель (при необходимости
смотрите статью определитель
матрицы: определение, методы вычисления,
примеры, решения):
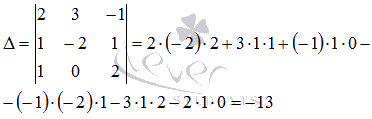 Так
как определитель основной матрицы
системы отличен от нуля, то система
имеет единственное решение, которое
может быть найдено методом Крамера.
Составим
и вычислим необходимые
определители
Так
как определитель основной матрицы
системы отличен от нуля, то система
имеет единственное решение, которое
может быть найдено методом Крамера.
Составим
и вычислим необходимые
определители ![]() (определитель
(определитель ![]() получаем,
заменив в матрице А первый
столбец на столбец свободных членов
получаем,
заменив в матрице А первый
столбец на столбец свободных членов ![]() ,
определитель
,
определитель ![]() -
заменив второй столбец на столбец
свободных членов,
-
заменив второй столбец на столбец
свободных членов, ![]() -
заменив третий столбец матрицы А на
столбец свободных членов):
-
заменив третий столбец матрицы А на
столбец свободных членов):
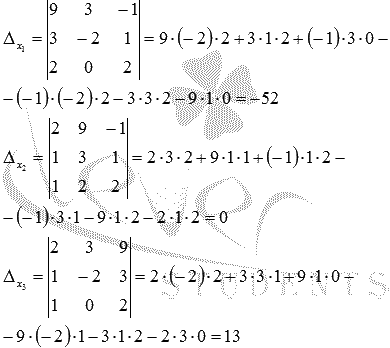 Находим
неизвестные переменные по
формулам
Находим
неизвестные переменные по
формулам 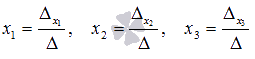 :
:
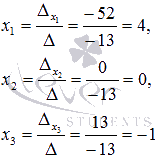 Ответ: x1 =
4, x2 =
0, x3 =
-1.
Основным
недостатком метода Крамера (если это
можно назвать недостатком) является
трудоемкость вычисления определителей,
когда число уравнений системы больше
трех.
Ответ: x1 =
4, x2 =
0, x3 =
-1.
Основным
недостатком метода Крамера (если это
можно назвать недостатком) является
трудоемкость вычисления определителей,
когда число уравнений системы больше
трех.
Решение
систем линейных алгебраических уравнений
матричным методом (с помощью обратной
матрицы).
Пусть
система линейных алгебраических
уравнений задана в матричной форме ![]() ,
где матрицаA имеет
размерность n на n и
ее определитель отличен от нуля.
Так
как
,
то матрица А –
обратима, то есть, существует обратная
матрица
,
где матрицаA имеет
размерность n на n и
ее определитель отличен от нуля.
Так
как
,
то матрица А –
обратима, то есть, существует обратная
матрица ![]() .
Если умножить обе части равенства
на
слева,
то получим формулу для нахождения
матрицы-столбца неизвестных переменных
.
Если умножить обе части равенства
на
слева,
то получим формулу для нахождения
матрицы-столбца неизвестных переменных ![]() .
Так мы получили решение системы линейных
алгебраических уравнений матричным
методом.
Пример.
Решите
систему линейных уравнений
матричным
методом.
Решение.
Перепишем
систему уравнений в матричной
форме:
.
Так мы получили решение системы линейных
алгебраических уравнений матричным
методом.
Пример.
Решите
систему линейных уравнений
матричным
методом.
Решение.
Перепишем
систему уравнений в матричной
форме:
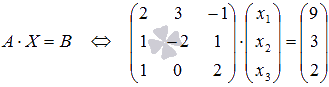 Так
как
то
СЛАУ можно решать матричным методом. С
помощью обратной матрицы решение этой
системы может быть найдено как
Так
как
то
СЛАУ можно решать матричным методом. С
помощью обратной матрицы решение этой
системы может быть найдено как 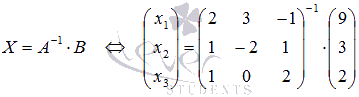 .
Построим
обратную матрицу
с
помощью матрицы из алгебраических
дополнений элементов матрицы А (при
необходимости смотрите статью методы
нахождения обратной матрицы):
.
Построим
обратную матрицу
с
помощью матрицы из алгебраических
дополнений элементов матрицы А (при
необходимости смотрите статью методы
нахождения обратной матрицы):
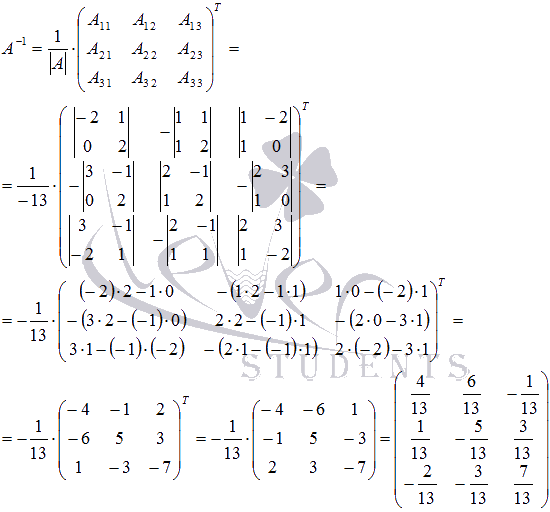 Осталось
вычислить
Осталось
вычислить 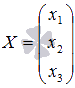 -
матрицу неизвестных переменных, умножив
обратную матрицу
-
матрицу неизвестных переменных, умножив
обратную матрицу  на
матрицу-столбец свободных членов
на
матрицу-столбец свободных членов  (при
необходимости смотрите статью операции
над матрицами):
(при
необходимости смотрите статью операции
над матрицами):
 Ответ:
Ответ: 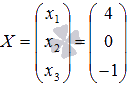 или
в другой записи x1 =
4, x2 =
0, x3 =
-1.
Основная
проблема при нахождении решения систем
линейных алгебраических уравнений
матричным методом заключается в
трудоемкости нахождения обратной
матрицы, особенно для квадратных матриц
порядка выше третьего.
или
в другой записи x1 =
4, x2 =
0, x3 =
-1.
Основная
проблема при нахождении решения систем
линейных алгебраических уравнений
матричным методом заключается в
трудоемкости нахождения обратной
матрицы, особенно для квадратных матриц
порядка выше третьего.
Решение
систем линейных уравнений методом
Гаусса.
Пусть
нам требуется найти решение системы
из n линейных
уравнений с n неизвестными
переменными 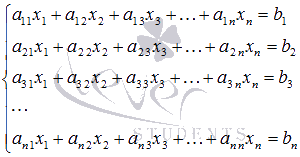 определитель
основной матрицы которой отличен от
нуля.
Суть
метода Гаусса состоит
в последовательном исключении неизвестных
переменных: сначала исключается x1 из
всех уравнений системы, начиная со
второго, далее исключается x2 из
всех уравнений, начиная с третьего, и
так далее, пока в последнем уравнении
останется только неизвестная переменная xn.
Такой процесс преобразования уравнений
системы для последовательного исключения
неизвестных переменных называется прямым
ходом метода Гаусса.
После завершения прямого хода метода
Гаусса из последнего уравнения
находится xn,
с помощью этого значения из предпоследнего
уравнения вычисляется xn-1,
и так далее, из первого уравнения
находится x1.
Процесс вычисления неизвестных переменных
при движении от последнего уравнения
системы к первому называется обратным
ходом метода Гаусса.
Кратко
опишем алгоритм исключения неизвестных
переменных.
Будем считать, что
определитель
основной матрицы которой отличен от
нуля.
Суть
метода Гаусса состоит
в последовательном исключении неизвестных
переменных: сначала исключается x1 из
всех уравнений системы, начиная со
второго, далее исключается x2 из
всех уравнений, начиная с третьего, и
так далее, пока в последнем уравнении
останется только неизвестная переменная xn.
Такой процесс преобразования уравнений
системы для последовательного исключения
неизвестных переменных называется прямым
ходом метода Гаусса.
После завершения прямого хода метода
Гаусса из последнего уравнения
находится xn,
с помощью этого значения из предпоследнего
уравнения вычисляется xn-1,
и так далее, из первого уравнения
находится x1.
Процесс вычисления неизвестных переменных
при движении от последнего уравнения
системы к первому называется обратным
ходом метода Гаусса.
Кратко
опишем алгоритм исключения неизвестных
переменных.
Будем считать, что ![]() ,
так как мы всегда можем этого добиться
перестановкой местами уравнений системы.
Исключим неизвестную переменную x1 из
всех уравнений системы, начиная со
второго. Для этого ко второму уравнению
системы прибавим первое, умноженное
на
,
так как мы всегда можем этого добиться
перестановкой местами уравнений системы.
Исключим неизвестную переменную x1 из
всех уравнений системы, начиная со
второго. Для этого ко второму уравнению
системы прибавим первое, умноженное
на ![]() ,
к третьему уравнению прибавим первое,
умноженное на
,
к третьему уравнению прибавим первое,
умноженное на ![]() ,
и так далее, к n-ому уравнению
прибавим первое, умноженное на
,
и так далее, к n-ому уравнению
прибавим первое, умноженное на ![]() .
Система уравнений после таких
преобразований примет вид
.
Система уравнений после таких
преобразований примет вид
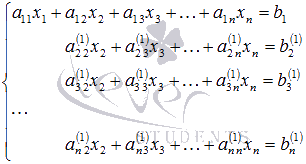 где
где 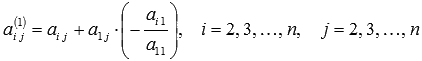 ,
а
,
а 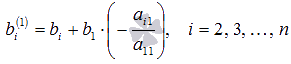 .
К
такому же результату мы бы пришли, если
бы выразили x1 через
другие неизвестные переменные в первом
уравнении системы и полученное выражение
подставили во все остальные уравнения.
Таким образом, переменная x1 исключена
из всех уравнений, начиная со второго.
Далее
действуем аналогично, но лишь с частью
полученной системы, которая отмечена
на рисунке
.
К
такому же результату мы бы пришли, если
бы выразили x1 через
другие неизвестные переменные в первом
уравнении системы и полученное выражение
подставили во все остальные уравнения.
Таким образом, переменная x1 исключена
из всех уравнений, начиная со второго.
Далее
действуем аналогично, но лишь с частью
полученной системы, которая отмечена
на рисунке
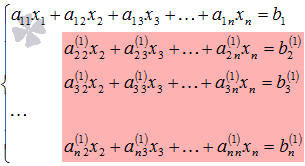 Будем
считать, что
Будем
считать, что ![]() (в
противном случае мы переставим местами
вторую строку с k-ой,
где
(в
противном случае мы переставим местами
вторую строку с k-ой,
где ![]() ).
Приступаем к исключению неизвестной
переменной x2 из
всех уравнений, начиная с третьего.
Для
этого к третьему уравнению системы
прибавим второе, умноженное на
).
Приступаем к исключению неизвестной
переменной x2 из
всех уравнений, начиная с третьего.
Для
этого к третьему уравнению системы
прибавим второе, умноженное на ![]() ,
к четвертому уравнению прибавим второе,
умноженное на
,
к четвертому уравнению прибавим второе,
умноженное на ![]() ,
и так далее, к n-ому уравнению
прибавим второе, умноженное на
,
и так далее, к n-ому уравнению
прибавим второе, умноженное на ![]() .
Система уравнений после таких
преобразований примет вид
.
Система уравнений после таких
преобразований примет вид
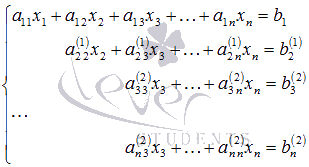 где
где 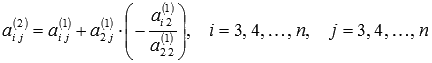 ,
а
,
а 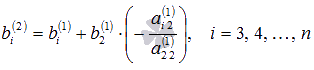 .
Таким образом, переменная x2 исключена
из всех уравнений, начиная с третьего.
Далее
приступаем к исключению неизвестной x3,
при этом действуем аналогично с отмеченной
на рисунке частью системы
.
Таким образом, переменная x2 исключена
из всех уравнений, начиная с третьего.
Далее
приступаем к исключению неизвестной x3,
при этом действуем аналогично с отмеченной
на рисунке частью системы
 Так
продолжаем прямой ход метода Гаусса
пока система не примет вид
Так
продолжаем прямой ход метода Гаусса
пока система не примет вид
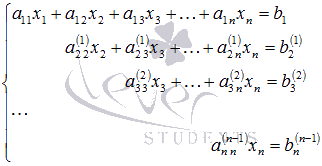 С
этого момента начинаем обратный ход
метода Гаусса: вычисляем xn из
последнего уравнения как
С
этого момента начинаем обратный ход
метода Гаусса: вычисляем xn из
последнего уравнения как 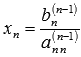 ,
с помощью полученного значения xn находим xn-1 из
предпоследнего уравнения, и так далее,
находим x1 из
первого уравнения.
Пример.
Решите
систему линейных уравнений
методом
Гаусса.
Решение.
Исключим
неизвестную переменную x1 из
второго и третьего уравнения системы.
Для этого к обеим частям второго и
третьего уравнений прибавим соответствующие
части первого уравнения, умноженные
на
,
с помощью полученного значения xn находим xn-1 из
предпоследнего уравнения, и так далее,
находим x1 из
первого уравнения.
Пример.
Решите
систему линейных уравнений
методом
Гаусса.
Решение.
Исключим
неизвестную переменную x1 из
второго и третьего уравнения системы.
Для этого к обеим частям второго и
третьего уравнений прибавим соответствующие
части первого уравнения, умноженные
на 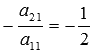 и
на
и
на 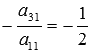 соответственно:
соответственно:
 Теперь
из третьего уравнения исключим x2,
прибавив к его левой и правой частям
левую и правую части второго уравнения,
умноженные на
Теперь
из третьего уравнения исключим x2,
прибавив к его левой и правой частям
левую и правую части второго уравнения,
умноженные на  :
:
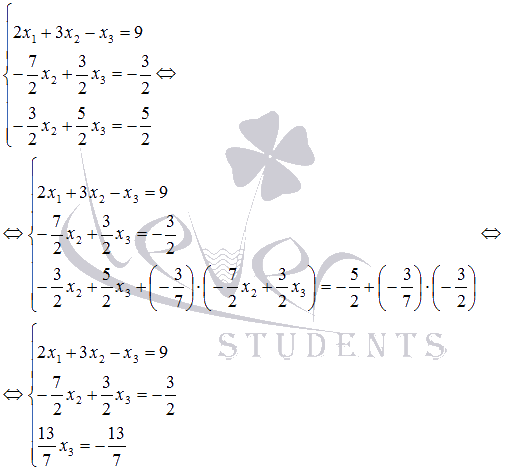 На
этом прямой ход метода Гаусса закончен,
начинаем обратный ход.
Из последнего
уравнения полученной системы уравнений
находим x3:
На
этом прямой ход метода Гаусса закончен,
начинаем обратный ход.
Из последнего
уравнения полученной системы уравнений
находим x3:
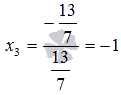 Из
второго уравнения получаем
Из
второго уравнения получаем 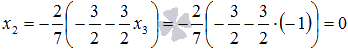 .
Из
первого уравнения находим оставшуюся
неизвестную переменную и этим завершаем
обратный ход метода Гаусса
.
Из
первого уравнения находим оставшуюся
неизвестную переменную и этим завершаем
обратный ход метода Гаусса ![]() .
Ответ: x1 =
4, x2 =
0, x3 =
-1.
.
Ответ: x1 =
4, x2 =
0, x3 =
-1.
Решение
систем линейных алгебраических уравнений
общего вида.
В
общем случае число уравнений системы p не
совпадает с числом неизвестных
переменных n:
 Такие
СЛАУ могут не иметь решений, иметь
единственное решение или иметь бесконечно
много решений. Это утверждение относится
также к системам уравнений, основная
матрица которых квадратная и
вырожденная.
Далее
нам потребуется понятие минора матрицы
и ранга матрицы, которые даны в статье ранг
матрицы: определение, методы нахождения,
примеры, решения.
Прежде
чем находить решение системы линейных
уравнений необходимо установить ее
совместность. Ответ на вопрос когда
СЛАУ совместна, а когда несовместна,
дает теорема
Кронекера – Капелли:
для
того, чтобы система из p уравнений
с n неизвестными
(p может
быть равно n)
была совместна необходимо и достаточно,
чтобы ранг основной матрицы системы
был равен рангу расширенной матрицы,
то есть, Rank(A)
= Rank(T).
Рассмотрим
на примере применение теоремы Кронекера
– Капелли для определения совместности
системы линейных уравнений.
Пример.
Выясните,
имеет ли система линейных
уравнений
Такие
СЛАУ могут не иметь решений, иметь
единственное решение или иметь бесконечно
много решений. Это утверждение относится
также к системам уравнений, основная
матрица которых квадратная и
вырожденная.
Далее
нам потребуется понятие минора матрицы
и ранга матрицы, которые даны в статье ранг
матрицы: определение, методы нахождения,
примеры, решения.
Прежде
чем находить решение системы линейных
уравнений необходимо установить ее
совместность. Ответ на вопрос когда
СЛАУ совместна, а когда несовместна,
дает теорема
Кронекера – Капелли:
для
того, чтобы система из p уравнений
с n неизвестными
(p может
быть равно n)
была совместна необходимо и достаточно,
чтобы ранг основной матрицы системы
был равен рангу расширенной матрицы,
то есть, Rank(A)
= Rank(T).
Рассмотрим
на примере применение теоремы Кронекера
– Капелли для определения совместности
системы линейных уравнений.
Пример.
Выясните,
имеет ли система линейных
уравнений 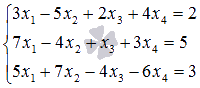 решения.
Решение.
Найдем
ранг основной матрицы системы
решения.
Решение.
Найдем
ранг основной матрицы системы  .
Воспользуемся методом окаймляющих
миноров. Минор второго порядка
.
Воспользуемся методом окаймляющих
миноров. Минор второго порядка 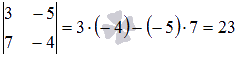 отличен
от нуля. Переберем окаймляющие его
миноры третьего порядка:
отличен
от нуля. Переберем окаймляющие его
миноры третьего порядка:
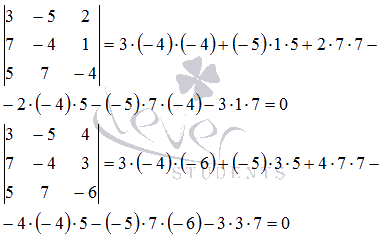 Так
как все окаймляющие миноры третьего
порядка равны нулю, то ранг основной
матрицы равен двум.
В свою очередь
ранг расширенной матрицы
Так
как все окаймляющие миноры третьего
порядка равны нулю, то ранг основной
матрицы равен двум.
В свою очередь
ранг расширенной матрицы 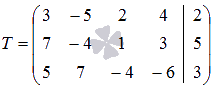 равен
трем, так как минор третьего
порядка
равен
трем, так как минор третьего
порядка
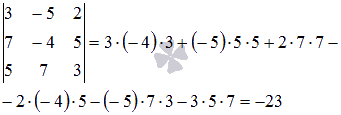 отличен
от нуля.
Таким образом, Rang(A)
< Rang(T),
следовательно, по теореме Кронекера –
Капелли можно сделать вывод, что исходная
система линейных уравнений
несовместна.
Ответ:
система решений не имеет.
отличен
от нуля.
Таким образом, Rang(A)
< Rang(T),
следовательно, по теореме Кронекера –
Капелли можно сделать вывод, что исходная
система линейных уравнений
несовместна.
Ответ:
система решений не имеет.
