
Алгебра-геометрия 01.09.12-08.11.12
Матрица 1
Определитель матрицы. 1
Свойства определителей. 3
Свойства обратной матрицы 5
Способы нахождения обратной матрицы 6
Точные (прямые) методы 6
Метод Гаусса—Жордана 6
С помощью матрицы алгебраических дополнений 6
Использование LU/LUP-разложения 6
Итерационные методы 7
Методы Шульца 7
Оценка погрешности 7
Выбор начального приближения 7
Примеры 8
Матрица 2х2 8
Транспонирование. 8
Системы линейных уравнений 9
Ранг матрицы 23
Матрица
Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы[1], в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.
Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае, количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами.
Определитель матрицы.
Определи́тель (или детермина́нт) — одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно). В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца.
Определитель матрицы А обозначается как: det(A), |А| или Δ(A).
Определитель (или детерминант1))
определяется для произвольной квадратной
матрицы ![]() ,
и представляет из себя полином от
всех ее элементов. Обозначается —
либо
,
и представляет из себя полином от
всех ее элементов. Обозначается —
либо ![]() ,
либо — в развернутом виде2) —
,
либо — в развернутом виде2) —

(матрица
ограничивается вертикальными чертами3)).
Имея в виду порядок матрицы
,
о ее определителе говорят как
об определителе
порядка ![]() .
.
Для ![]() :
:
![]()
для ![]() :
:
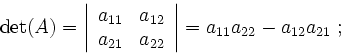
для ![]() :
:

![]()
для ![]() формула становится
громоздкой.
формула становится
громоздкой.
Главная цель введения понятия определителя: с помощью этой функции устанавливаются условия существования от нескольких переменных; более того, эта функция позволяет компактно записать решение. Определитель имеет также ряд геометрических приложений.
Введем теперь определитель произвольного порядка .
Упорядоченная
пара различных натуральных
чисел ![]() образует инверсию (или
нарушение порядка), если
образует инверсию (или
нарушение порядка), если ![]() .
Будем обозначать число инверсий в
паре
через
.
Будем обозначать число инверсий в
паре
через ![]() .
Таким образом
.
Таким образом
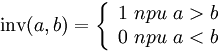
Число
инверсий в последовательности различных
натуральных чисел ![]() определяется
следующим образом:
определяется
следующим образом:
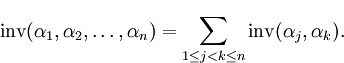
П
Пример.
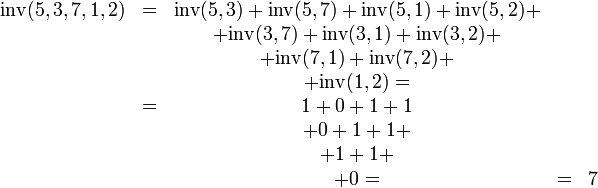
?
Показать,
что ![]() .
.
Определителем (или детерминантом) матрицы

называется величина
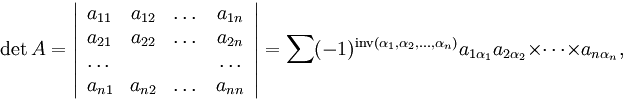
где
сумма распространяется на
всевозможные перестановки ![]() элементов
элементов ![]() .
В общем случае сумма, определяющая
определитель порядка
,
содержит
.
В общем случае сумма, определяющая
определитель порядка
,
содержит ![]() слагаемых,
каждое из которых представляет
произведение
элементов
определителя, взятых по одному из каждой
строки определителя и из каждого его
столбца (т.е. после того, как в произведение
вставляется элемент
слагаемых,
каждое из которых представляет
произведение
элементов
определителя, взятых по одному из каждой
строки определителя и из каждого его
столбца (т.е. после того, как в произведение
вставляется элемент ![]() больше
в это же произведение не берется ни
одного элемента из
больше
в это же произведение не берется ни
одного элемента из ![]() -й
строки и
-й
строки и ![]() -го
столбца). Знак у произведения определяется
по указанному выше правилу и можно
доказать, что половина слагаемых в сумме
будет иметь положительный знак, а другая
половина — отрицательный.
-го
столбца). Знак у произведения определяется
по указанному выше правилу и можно
доказать, что половина слагаемых в сумме
будет иметь положительный знак, а другая
половина — отрицательный.
Свойства определителей.
СВОЙСТВО 1. Величина определителя не изменится, если все его строки заменить столбцами, причем каждую строку заменить столбцом с тем же номером, то есть
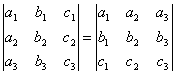 .
.
СВОЙСТВО 2. Перестановка двух столбцов или двух строк определителя равносильна умножению его на -1. Например,
 .
.
СВОЙСТВО 3. Если определитель имеет два одинаковых столбца или две одинаковые строки, то он равен нулю.
СВОЙСТВО 4. Умножение всех элементов одного столбца или одной строки определителя на любое число k равносильно умножению определителя на это число k. Например,
 .
.
СВОЙСТВО 5. Если все элементы некоторого столбца или некоторой строки равны нулю, то сам определитель равен нулю. Это свойство есть частный случае предыдущего (при k=0).
СВОЙСТВО 6. Если соответствующие элементы двух столбцов или двух строк определителя пропорциональны, то определитель равен нулю.
СВОЙСТВО 7. Если каждый элемент n-го столбца или n-й строки определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один в n-м столбце или соответственно в n-й строке имеет первые из упомянутых слагаемых, а другой - вторые; элементы, стоящие на остальных местах, у вех трех определителей одни и те же. Например,
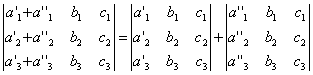
СВОЙСТВО 8. Если к элементам некоторого столбца (или некоторой строки) прибавить соответствующие элементы другого столбца (или другой строки), умноженные на любой общий множитель, то величина определителя при этом не изменится. Например,
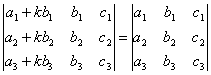 .
.
Дальнейшие свойства определителей связаны с понятием алгебраического дополнения и минора. Минором некоторого элемента называется определитель, получаемый из данного путем вычеркиванием строки и столбца, на пересечении которых расположен этот элемент.
Алгебраическое дополнение любого элемента определителя равняется минору этого элемента, взятому со своим знаком, если сумма номеров строки и столбца, на пересечении которых расположен элемент, есть число четное, и с обратным знаком, если это число нечетное.
Алгебраическое дополнение элемента мы будем обозначать большой буквой того же наименования и тем же номером, что и буква, кторой обозначен сам элемент.
СВОЙСТВО 9. Определитель
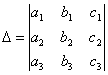
равен сумме произведений элементов какого-либо столбца (или строки) на их алгебраические дополнения.
Иначе говоря, имеют место следующие равенства:
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Обра́тная ма́трица — такая матрица A−1, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:
![]()
Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдо обратные матрицы, похожие на обратные по многим свойствам.
Свойства обратной матрицы
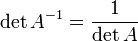 ,
где
,
где 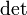 обозначает определитель.
обозначает определитель.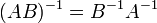 для
любых двух обратимых матриц
для
любых двух обратимых матриц 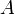 и
и 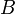 .
.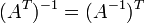 где
где 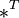 обозначает
транспонированную матрицу.
обозначает
транспонированную матрицу.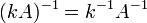 для
любого коэффициента
для
любого коэффициента 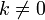 .
.Если необходимо решить систему линейных уравнений
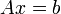 ,
(b — ненулевой вектор) где
,
(b — ненулевой вектор) где 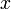 —
искомый вектор, и если
—
искомый вектор, и если 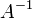 существует,
то
существует,
то 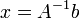 .
В противном случае либо
размерность пространства решений
больше нуля, либо их нет вовсе.
.
В противном случае либо
размерность пространства решений
больше нуля, либо их нет вовсе.
Способы нахождения обратной матрицы
Если матрица обратима, то для нахождения обратной матрицы можно воспользоваться одним из следующих способов:
Точные (прямые) методы
Метод Гаусса—Жордана
Возьмём две матрицы: саму A и единичную E. Приведём матрицу A к единичной матрице методом Гаусса—Жордана. После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A−1.
При
использовании метода Гаусса первая
матрица будет умножаться слева на одну
из элементарных матриц ![]() (трансвекциюили диагональную
матрицу с
единицами на главной диагонали, кроме
одной позиции):
(трансвекциюили диагональную
матрицу с
единицами на главной диагонали, кроме
одной позиции):
![]() .
.
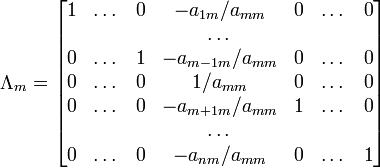 .
.
Вторая
матрица после применения всех операций
станет равна ![]() ,
то есть будет искомой. Сложность
алгоритма —
,
то есть будет искомой. Сложность
алгоритма — ![]() .
.
