Принципы суммы рангов и гарантированного результата.

Если не учитывать весовые коэффициенты (веса целей, вероятности ситуаций, веса экспертов), т.е. предполагать, что все оценочные параметры имеют одинаковые приоритеты, то можно использовать принципы суммы рангов и гарантированного результата.

В 1 случае в общей таблице, составленной из всех таблиц-ранжировок , представленных экспертами суммируются ранги. Затем по величине этих сумм осуществляется ранжирование решений. Самой меньшей сумме соответствует наиболее приоритетное решение. Следующей по величине сумме - решение, менее приоритетное предыдущего, но более приоритетного остальных. Решения, имеющие одинаковые суммы рангов, будут эквивалентны и имеют одинаковый ранг.

I эксперт

	С1	С2	С3	С4	С5
А1	1	2	1	3	2
А2	2	1	2	2	2
А3	3	2	3	1	1

2 Эксперт

	С1	С2	С3	С4	С5
А1	2	1	2	2	2
А2	1	2	1	1	1
А3	3	2	3	2	2

	С1	С2	С3	С4	С5	С1	С2	С3	С4	С5
А1	1	2	1	3	2	2	1	2	2	2	18
А2	2	1	2	2	2	1	2	1	1	1	15
А3	3	2	3	1	1	3	2	3	2	2	22

А2>A1>A3

Выбираем А2

Принцип гарантированного результата.

Принцип гарантированного результата соответствует осторожной стратегии поведения, его можно назвать критерием пессимизма. В каждой строке общей таблицы ранжировок выбирается худшее предпочтение (наибольшее значение ранга). Далее среди худших оценок выбирается минимальное значение ранга и соответствующее ему решение представляется в качестве наиболее предпочтительного. (среди возможных худших вариантов выбирается лучший).

	С1	С2	С3	С4	С5	С1	С2	С3	С4	С5		Наибольный ранг
А1	1	2	1	3	2	2	1	2	2	2	18	3
А2	2	1	2	2	2	1	2	1	1	1	15	2 А2
А3	3	2	3	1	1	3	2	3	2	2	22	3

А2>A1эквивалент.A3

(212)

Принцип «метод медианы»

Под медианной ранжировкой понимается обобщенная ранжировка, которая согласуется со всеми ранжировками, полученными в результате экспертного оценивания. При этом учитываются все весовые коэффициенты. Вероятности, которые фигурируют при описании проблемной ситуации .

Для нахождения меридианной ранжировки введем понятие матрицы парных сравнений.

Правило построения:

Пусть n целей:

C1,C2… Cn

m –вариантов решений

A1,A2,… Am

Каждой цели соответствует ранжировка решений (альтернатив)

R1, r2… rm –ранжировка решений по цели С

	C
A1	R1
A2	R2
An	Rm

Каждой ранжировке соответствует матрица парных сравнений, такая , что ее элементами являются 1 или 0 в соответствии с правилом.

1 ,если r_i <=r_k

X_ik= 0, если r_i >r_k

r_i - ранжировка решений А_i

r_k – ранжировка решений А_к

r1 r2 r3

( 1 2 3)

1 1 1

0 1 1 матрица парных сравнений

0 0 1

( 2 1 2)

1 0 1

1 1 1

1 0 1

Между матрицами парных сравнений можно вычислить «расстояние», его смысл состоит в том, что оно совпадает с числом поразрядных несовпадений двух матриц парных сравнений.

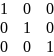
m*n

m²-m=(m-1) – расстояние

Минимальное расстояние соответствует одинаковым матрицам парных сравнений (ранжировкам) и = 0 . Максимальное расстояние соответствует противоположным ранжировкам и = m(m-1) (m единиц на главной диагонали всегда совпадают).

Определим такую матрицу парных сравнений, которая наилучшим образом согласуется с имеющимися n – матрицами парных сравнений в следующем смысле:

	C1	C2	…	Сn
A1	R1	R12		R1n
A2	R2	R22		R2n
An	Rm	Rm2		Rmn

( r₁¹, r₂¹ , … r_m¹) - = (x_ik^I)

(r₁^s r₂^s … r_m^s )  (x_ik^s)

Медианная матрица

(x_ik^med)

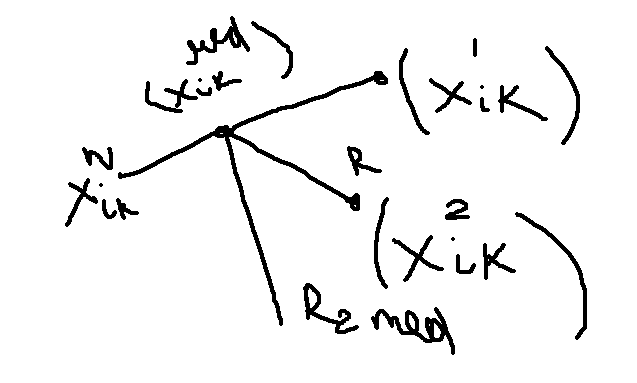
Min= ∑ R s, med

Медианная матрица удовлетворяет следующему свойству: сумма расстояний от каждой матрицы (ранжировки) до матрицы-медианы является минимальной.

если цели имеют различные коэффициенты относительной важности или веса

β_s – веса целей (s=1,2,3,…,n)

∑β=1

В этом случае медиана определяется как минимальная взвешенная сумма расстояний от каждой ранжировки до медианной матрицы.

Min ∑βs, med

βs, med – взвешенное расстояние между матрицей (x_ik^s) и медианой матрицы (x_ik^med)

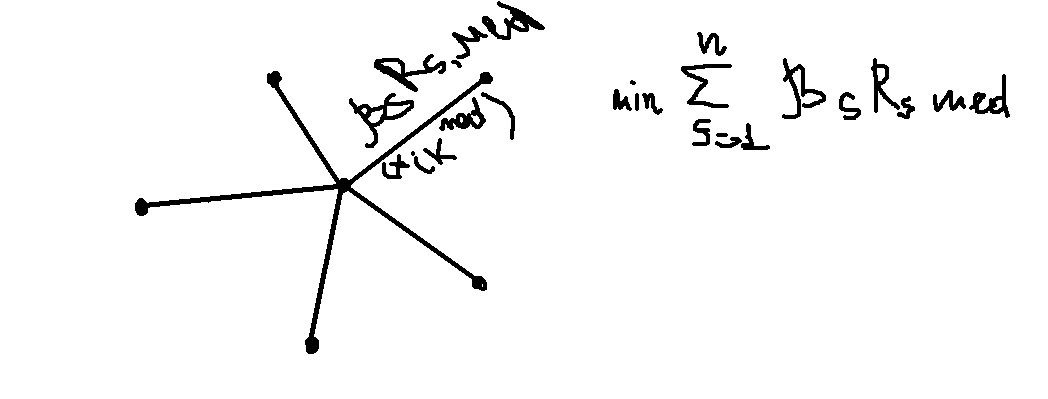
Условно медианную ранжировку можно представить как центр тяжести мнений относительно предпочтительности решений, отраженных в каждой ранжировке с учетом её веса. Медиана «будет ближе» к ранжировкам, имеющим большие веса и дальше от ранжировок с меньшими весами.

В качестве весовых характеристик выступают следующие величины:

W_i¹ – веса цели (i=1…n)

P_j – вероятности ситуаций

V_k – веса экспертов

∑W_i¹=1

∑P_j¹=1

∑Vk¹=1

β=вес цели*вероятность ситуации*вес эксперта