2.2Определение температурного режима колонны.
При заданном составе паровой, жидкой или парожидкостной смеси и фиксированном давлении в системе температура, составляющая равновесию в таких условиях, определяется расчетом.
Температура верха колонны определяется из уравнения изотермы паровой фазы:
=
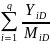1 (15)
Где,
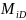– коэффициент распределения (константа
фазового равновесия); i-того
компонента при температуре и давлении
наверху колонны;
– мольная доля компонента в паре наверху
колонны, в случае полной конденсации
паров в дефлегматоре
=
;
q–
число компонентов смеси.
Температура внизу колонны определяется из уравнения изотермы жидкой фазы:
=
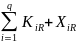1 (16)
Где,
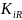– коэффициент распределения i-того
компонента при температуре и давлении
низа колонны.
Если
сырье поступает в колонну при температуре
начала кипения смеси, т.е. доля отгона
сырья на входе в колонну e=0,
температура сырья
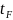определяется по уравнению изотермы
жидкой фазы (16). Если сырье поступает в
колонну при температуре конца кипения
смеси, доля отгона е=1,температура сырья
определяется по уравнению изотермы
паровой фазы (15). Если сырье поступает
в колонну в виде парожидкостной смеси,
т.е.
,
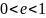температура сырья на входе в колонну
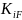определяется из уравнения:
=
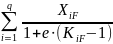1 (17)
или
=
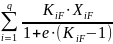1 (18)
Где, - коэффициент распределения i-того компонента смеси при температуре и давлении в зоне питания колонны.
Уравнение
(17) лучше использовать при доле отгона
е=0,5, а уравнение (18) дает лучший результат
при доле отгона е
0,5.
Коэффициенты
распределения
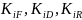зависят от температуры, поэтому уравнение
(15) - (18) при расчете температур
,
,
решаются методом последовательного
приближения.
2.3.Построение диаграммы фазового равновесия.
В процессах перегонки и ректификации равновесные концентрации фаз определяются зависимостью:
=
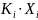(19)
Где,
- мольная концентрация i-того
компонента в паре, равновесном с жидкостью
состава
.
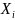В
случае, когда разделяемую смесь можно
считать идеальной, т.е. для всех компонентов
смеси выполняется закон Раули, коэффициент
распределения
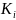рассчитывается как отношение давления
насыщенного пара компонента
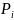при ректификационной температуре к
общему давлению в системе П:
=
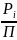(20)
Для идеальных смесей зависимость между равновесными составами фаз выражается уравнением Рауля-Дальтона:
=
(21)
Для многих жидких смесей расчет коэффициента распределения можно производить по уравнению (20), если общее давление в системе П 0,49 Па (5ат.).
Давление насыщенных паров индивидуальных веществ или зависимости для их расчета приведены в работах [1-6].
Для
бинарных смесей, подчиняющихся закону
Рауля, диаграмму фазового равновесия
в координатах у-х (рис.2) строят по
следующему алгоритму. Температурный
интервал выкипания разделяемой смеси
определяется, как разность температур
кипения чистого низкокипящего
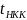и чистого высококипящего
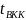компонентов при выбранном давлении в
системе П. В этом интервале температур
от
до
принимается ряд значений температуры
(обычно десяти значений бывает достаточно);
для каждой температуры определяется
значение насыщенных паров компонентов
и рассчитывается из соотношения (20)
коэффициенты распределения низкокипящего
компонента. Из соотношения (22) рассчитывается
мольная концентрация низкокипящего
компонента
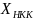в жидкости, кипящей при выбранной
температуре и давлении П:
=
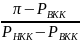
Где,
,
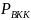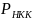– давление насыщенных паров высококипящего
и низкокипящего компонентов.
После
этого из соотношения (21)определяется
мольная концентрация низкокипящего
компонента в паре
,
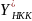равновесном с жидкостью. Далее строится
диаграмма фазового равновесия в
координатах у-х (см. рис.2).
В
тех случаях, когда для компонентов
разделяемой смеси наблюдаются значительные
отклонения от закона Рауля, приведенный
выше алгоритм вычисления равновесной
паровой и жидкой фаз сохраняется,
изменяется лишь способ расчета
коэффициента распределения
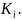
Рис.2. Диаграмма фазового равновесия бинарной смеси в координатах у-х.
В работе [9] рассмотрены методы расчета для смесей, не подчиняющихся закону Рауля. С целью облегчения расчетов разработаны различные монограммы для определения коэффициента распределения [6, 10], в частности, для ориентировочных расчетов широко используется номограмма Де-Пристера [5, 9]. Для многих бинарных смесей равновесные составы паровой и жидкой фаз приведены в работе [11].