Период колебаний физического маятника

Для того, чтобы найти период колебаний физического маятника, необходимо решить уравнение качания. Для этого умножим левую   и правую часть этого уравнения на  . Тогда:

.

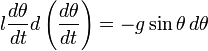Интегрируя это уравнение, получаем.

,

где   произвольная постоянная. Её можно найти из граничного условия, что в моменты  . Получаем:  . Подставляем и преобразовываем получившееся уравнение:

.

Отделяем переменные и интегрируем это уравнение:

.

Удобно сделать замену переменной, полагая  . Тогда искомое уравнение принимает вид:

.

Здесь   — нормальный эллиптический интеграл Лежандра 1-го рода. Для периода колебаний получаем формулу:

.

Здесь   — полный нормальный эллиптический интеграл Лежандра 1-го рода. Раскладывая его в ряд, можно получить удобную для практических вычислений формулу:

.

[Править]Период малых колебаний физического маятника

Если амплитуда колебаний   мала, то корень в знаменателе эллиптического интеграла приближенно равен единице. Такой интеграл легко берется, и получается хорошо известная формула малых колебаний:

.

Эта формула даёт результаты приемлемой точности (ошибка менее 1 %) при углах, не превышающих 4°.

Следующий порядок приближения можно использовать с приемлемой точностью (ошибка менее 1 %) при углах до 1 радиана (≈60°)

.

Вопрос 4. Энергия гармонических колебаний

        При механических колебаниях колеблющееся тело (или материальная точка) обладает кинетической и потенциальной энергией. Кинетическая энергия тела W:

(Скорость тела v = ds/dt)

        Для вычисления потенциальной энергии тела воспользуемся самой общей формулой, связывающей силу и потенциальную энергию тела в поле этой силы:

где U - потенциальная энергия, набираемая (или теряемая) телом, движущимся в силовом поле F от точки 0 (точки, в которой потенциальная энергия принимается равной 0) до точки х.

        Для силы, линейно зависящей от смещения (как в случае наших механических маятников, такие силы носят общее название квазиупругих сил) мы имеем:

Сравнивая формулы

для кинетической и потенциальной энергии механического маятника, можно сделать следующие выводы:

1. Полная механическая энергия тела не изменяется при колебаниях:    2. Частота колебаний кинетической и потенциальной энергии в 2 раза больше частоты колебаний маятника.  3. Колебания кинетической и потенциальной энергии сдвинуты друг относительно друга по фазе на  (на полпериода). Когда кинетическая энергия достигает максимума, потенциальная - минимума (нуля) и наоборот. Энергия при колебаниях постоянно перекачивается из потенциальной в кинетическую и обратно.

Вопрос 5.

Ускоре́ние свобо́дного паде́ния g (оно же ускорение силы тяжести), — ускорение, придаваемое телу в вакууме силой тяжести, то есть геометрической суммой гравитационногопритяжения планеты (или другого астрономического тела) и сил инерции, вызванных её вращением, за исключением кориолисовых сил инерции^[1]. В соответствии со вторым законом Ньютона, ускорение свободного падения численно равно силе тяжести, воздействующей на объект единичной массы.

Значение ускорения свободного падения на поверхности Земли обычно принимают равным 9,8 или 10 м/с². Стандартное («нормальное») значение, принятое при построении систем единиц, g = 9,80665 м/с²^[2], а в технических расчётах обычно принимают g = 9,81 м/с².

Стандартное значение g было определено как «среднее» в каком-то смысле ускорение свободного падения на Земле, примерно равно ускорению свободного падения на широте45,5° на уровне моря.

Реальное ускорение свободного падения на поверхности Земли зависит от широты, времени суток и других факторов. Оно варьируется от 9,780 м/с² на экваторе до 9,832 м/с² наполюсах^[3]. Оно может быть вычислено (в м/с²) по эмпирической формуле:

где   — широта рассматриваемого места,   — высота над уровнем моря в метрах.^[4] Эта формула применима лишь в ограниченном диапазоне высот от 0 до нескольких десятков км, где убывание ускорения свободного падения с высотой можно считать линейным (на самом же деле оно убывает квадратично).

Как в лабораторке измеряли я хз ибо проебал^^