Обчислення критерію для нормального розподілу.

Нехай інтервальний статистичний розподіл задається таблицею

Нехай рівень значимості дорівнює .

Треба перевірити гіпотезу про нормальний розподіл генеральної сукупності.

Нехай середини інтервалів .

Для розрахунку теоретичних частот розраховується ряд допоміжних величин , , , .

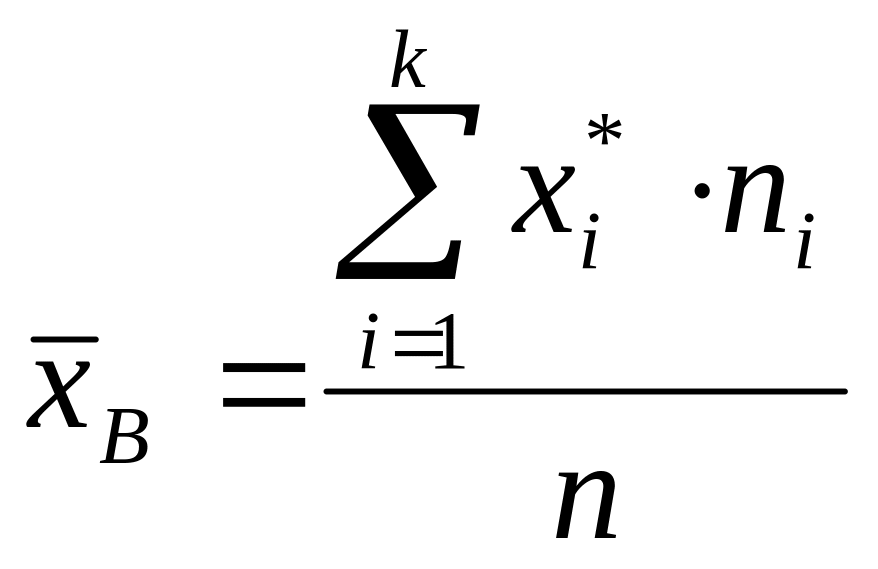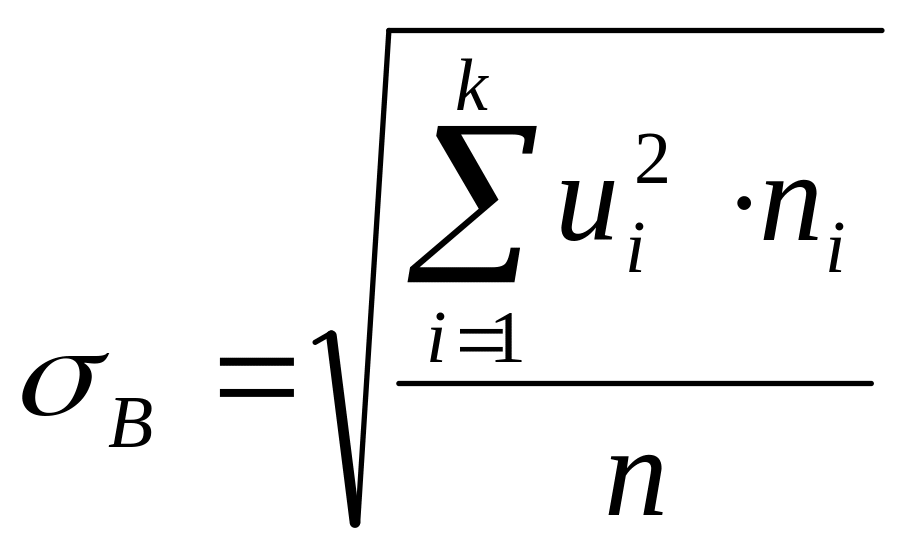Тоді теоретичні частоти , де .

Розраховується , де .

Для нормального розподілу кількість параметрів дорівнює 2, таким чином , звідси .

По числам та знаходимо число .

Розрахунки оформлюються у вигляді таблиці:

1

Критерій Колмогорова. Параметричні гіпотези

Параметричні гіпотези це гіпотези про значення або властивості ознак генеральної сукупності.

Для перевірки таких гіпотез розглядають варіаційний ряд :

На основі його аналізу пропонують гіпотезу про те, що

Критерій Стьюдента Критерій Фішера.

Критерій Кохрена (Cochran)

Критерій Кохрена був запропонований в 1941 році в роботі

Cochran W. G. The distribution of the largest of a set of estimated variances as a fraction of their total // Annals of Eugenics. 1941. V. 11. P. 47-52.

Нехай дано k вибірок рівного об’єму n.

вибіркова оцінка дисперсії -ї вибірки, яка обчислюється за формулою

.

Треба, для рівня значимості перевірити гіпотезу про те що дисперсії всіх вибірок рівні.

Спостережуване значення критерію Ко хрена обчислюються за формулою:

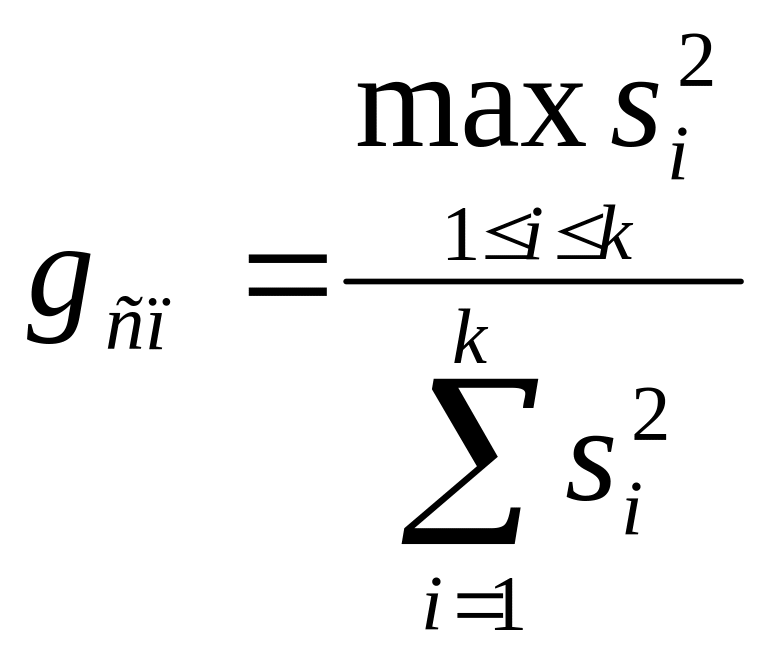
Критичне значення критерію Кохрена для рівня значимості визначається з формули:

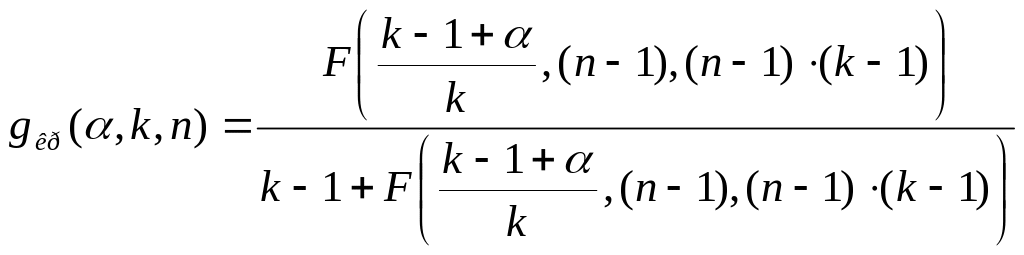
Значення функції визначається або з спеціальних таблиць для оберненої функції розподілу Фішера-Снедекора, або шляхом використання спеціальної статистичної функції Excel FРАСПОБР .

Якщо то нульова гіпотеза відхиляється.

Приклад використання критерію Кохрена.

Нехай є декілька однакових станків для свердління, і треба перевірити чи працюють вони з однаковою точністю. Для цього на всіх станках роблять однакову кількість отворів рівного діаметра. Вимірюють отримані отвори і складають з цих величин вибірку для кожного станка. До даної вибірки застосовують критерій Кохрена.