Побудова довірчого інтервалу для генерального середнього при невідомому значенні генерального середнього квадратичного відхилення із заданою надійністю .

Нехай дискретний статистичний розподіл задається таблицею

і нехай ознака генеральної сукупності має нормальний закон розподілу.

Нехай

об’єм вибірки

вибіркова середня

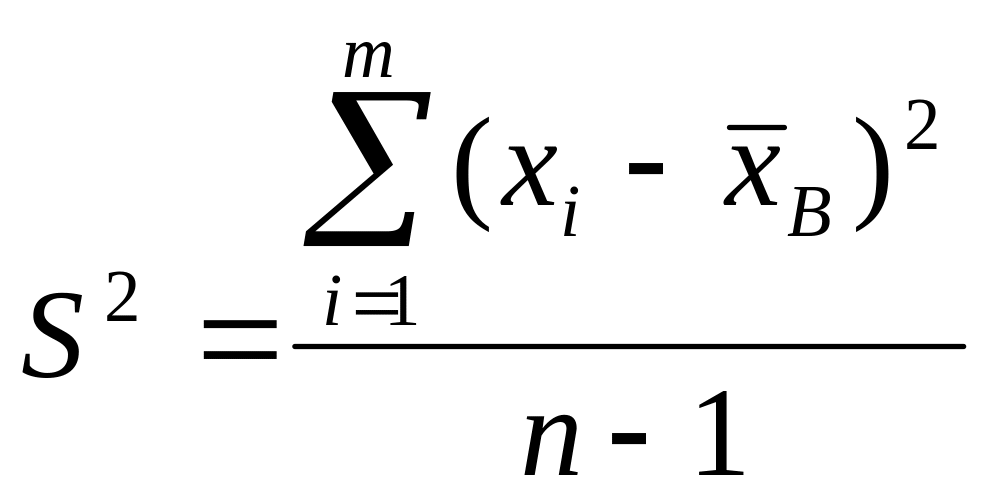виправлена дисперсія

надійність

Для побудови довірчого інтервалу для генерального середнього при невідомому значенні генерального середнього квадратичного відхилення із заданою надійністю застосовується випадкова величина

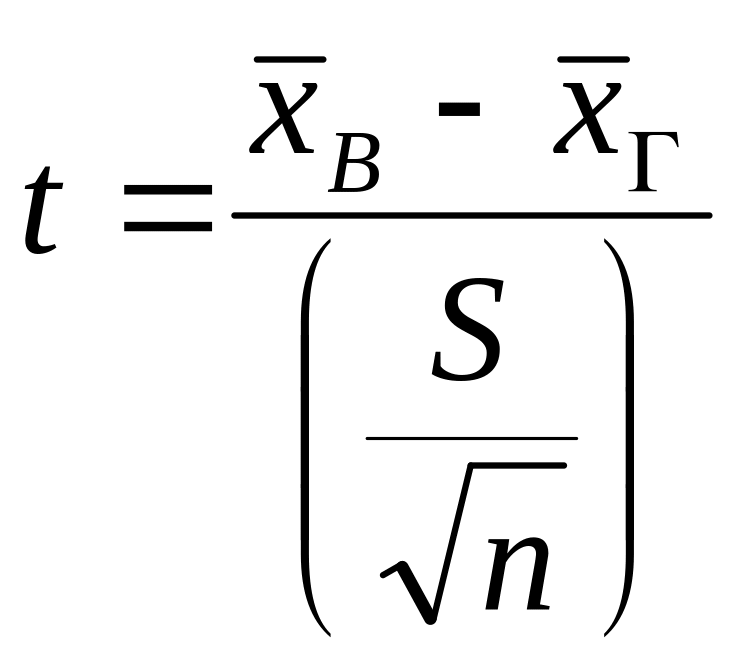
Вона має розподіл Стьюдента з ступенями свободи.

Нагадаємо, що випадкова величина має розподіл Стьюдента з ступенями свободи якщо її щільність має вигляд

,

де гамма-функція.

Основні числові характеристики.

Рівняння 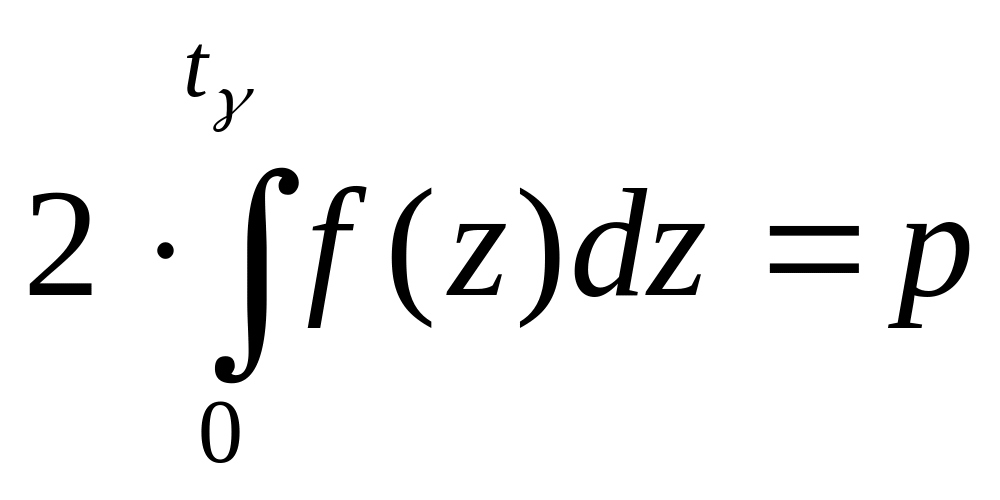у випадку коли об’єм вибірки дорівнює n може бути розв’язане або за допомогою спеціальних таблиць, або за допомогою функції Excel СТЬЮДРАСПОБР((1-p),(n-1))

Нехай розв’язок рівняння

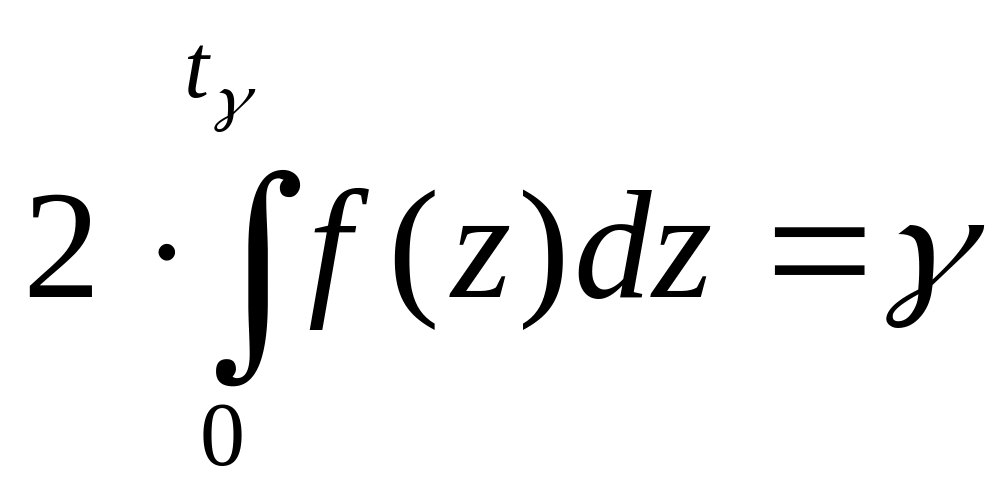
Тоді довірчий інтервал для генерального середнього , у випадку коли ознака генеральної сукупності не обов’язково має нормальний закон розподілу, при невідомому значенні середнього квадратичного відхилення із заданою надійністю і відомому об’ємі вибірки має вигляд: де точність інтервальної оцінки.

Побудова довірчого інтервалу для генеральної дисперсії і

середнього квадратичного відхилення із заданою надійністю.

***************************************************************

СТАТИСТИЧНІ ГІПОТЕЗИ

Основні поняття

Поняття статистичної гіпотези. Параметричні і непараметричні статистичні гіпотези. Нульова та конкуруюча гіпотеза. Помилки першого та другого роду. Рівень значимості. Статистичний критерій. Потужність критерію.

Критична область. Область прийняття гіпотези. Критичні межі. Односторонні та двосторонні критичні області.

Статистичною гіпотезою називають будь-яке твердження про вид або властивості розподілу випадкової величини, що спостерігається в експерименті.

Статистична гіпотеза називається параметричною статистичною гіпотезою якщо це є гіпотеза про значення, або властивості параметрів ознак генеральної сукупності.

Статистична гіпотеза називається непараметричною статистичною гіпотезою якщо це є гіпотеза про закон розподілу ознаки генеральної сукупності.

Нульовою (основною) гіпотезою називають висунуту гіпотезу .

Конкуруючою (альтернативною) гіпотезою називають гіпотезу (або ) яка суперечить нульовій.

Математична статистика не дає рекомендацій щодо вибору нульової гіпотези.

Цей вибір повністю визначається дослідником і залежить від постановки задачі.

Помилкою першого роду називають помилку яка полягає в тому, що гіпотеза відхиляється у випадку, коли вона справедлива.

Рівнем значимості називають ймовірність допущення помилки першого роду, її позначають .

Стандартні рівні значимості: 0,1; 0,05; 0,01; 0,001.

Помилкою другого роду називають помилку яка полягає в тому, що гіпотеза приймається у випадку, коли вона несправедлива.

Ймовірність помилки другого роду позначають через .

Статистичний критерій це оціночний показник, обчислений на основі фактичних спостережень, відповідно до якого приймають або відхиляють нульову гіпотезу.

Статистичний критерій позначають .

Потужністю критерію називають ймовірність того, що нульова гіпотеза відхиляється, якщо справедлива конкуруюча.

Потужність критерію дорівнює .

Критичною областю називають підмножину всіх можливих значень статистичного критерію, при яких гіпотеза відхиляється. Її позначають .

Критичні області будують таким чином, щоб потужність критерію була максимальною.

Областю прийняття гіпотези називають підмножину всіх можливих значень статистичного критерію, при яких гіпотеза приймається. Її позначають .

Критичними межами (критичними точками) називають межі множини (або ).

Критичні точки визначаються з спеціальних таблиць, або розраховуються на комп’ютері.

Критичні точки позначаються (або якщо їх кілька).

Критична область називається односторонньою якщо вона має вигляд: (лівостороння критична область) або (правостороння критична область).

Критична область називається двосторонньою якщо вона має вигляд: .