Емпірична функція для інтервального статистичного розподілу та її властивості.

Відносною частотою класового інтервалу називають число , де .

Накопиченими частотами називають числа

Тепер ми можемо дати означення інтервального статистичного розподілу вибірки:

Функція аргументу , що визначає відносну частоту події називається емпіричною функцією інтервального статистичного розподілу або комулятою.

При побудові комуляти для інтервального статистичного розподілу вибірки за основу береться припущення, що ознака на кожному частинному інтервалі має рівномірну щільність ймовірностей, тому у проміжках , для , є лінійною функцією.

Властивості функції :

2. де найменша варіанта варіаційного ряду

3. де найбільша варіанта варіаційного ряду

4. У проміжках , для , є лінійною функцією, яка визначається з умови , .

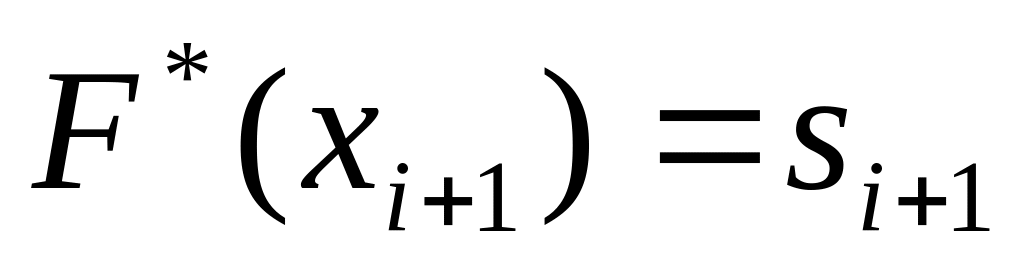5. є неспадною функцією

6. є неперервною функцією

Властивості 4 та 6 показують різницю у властивостях для інтервальних та дискретних статистичних розподілів.

Числові характеристики інтервального статистичного розподілу вибірки.

Медіаною інтервального статистичного розподілу називається число для якого виконується умова .

Для обчислення треба знайти такий інтервал , для якого і . Цей інтервал називають медіанним частковим інтервалом. Якщо такий інтервал знайдений тоді обчислюється за формулою:

Мода інтервального статистичного розподілу

де

- початок модального інтервалу

- частота модального інтервалу

- частота домодального інтервалу

- частота післямодального інтервалу

Вибіркова середня, дисперсія та середнє квадратичне відхилення для інтервального статистичного розподілу визначається шляхом переходу від інтервального до дискретного статистичного розподілу, варіантами якого є середини часткових інтервалів .

Відповідний дискретний статистичний ряд буде мати вигляд:

Вибірковою середньою інтервального статистичного розподілу називається число

Дисперсією інтервального статистичного розподілу називається число

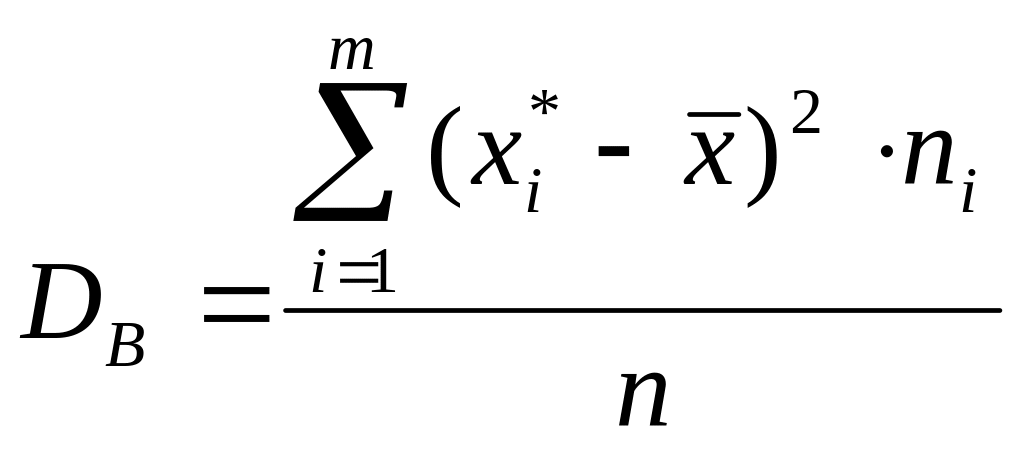
Середнім квадратичним відхиленням інтервального статистичного розподілу називається число

Графічне зображення інтервальних статистичних розподілів: гістограма частот, графік комуляти інтервального статистичного розподілу.

Нехай інтервальний статистичний розподіл задається таблицею

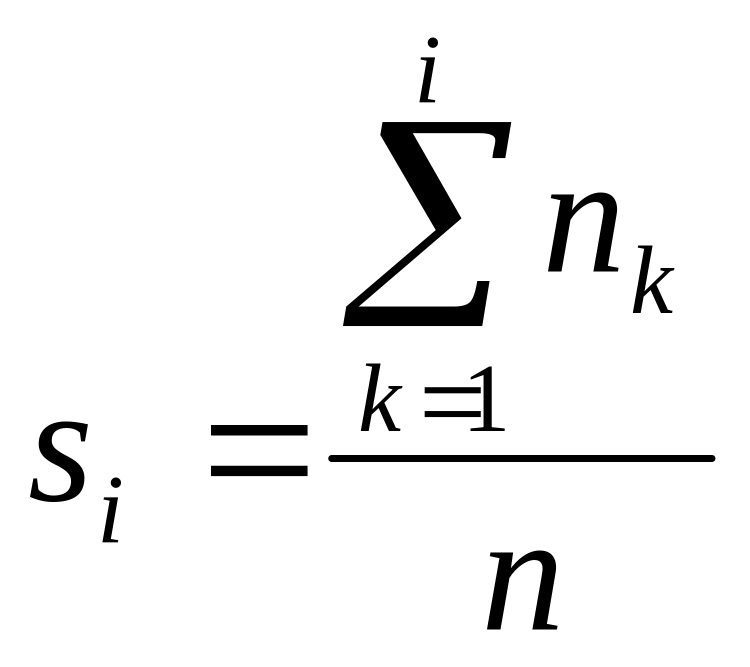накопичені частоти.

Гістограмою частот інтервального статистичного розподілу називається фігура що складається з прямокутників кожний з яких має основу і висоту, що дорівнює .

Гістограму частот інтервального статистичного розподілу розташовують на координатній площині , основа -го прямокутника відповідає відрізку .

При побудові комуляти для інтервального статистичного розподілу вибірки за основу береться припущення, що ознака на кожному частинному інтервалі має рівномірну щільність ймовірностей. Тому комулята інтервального статистичного розподілу має вигляд ламаної лінії яка ( в межах ) послідовно з’єднує точки , для вона співпадає з віссю абсцис, а для вона співпадає з прямою .

СТАТИСТИЧНІ ОЦІНКИ

Поняття статистичної оцінки.

Параметри генеральної сукупності є величинами сталими, але їх числове значення невідоме. Ці параметри оцінюються параметрами вибірки.

Якщо параметр генеральної сукупності, відповідну йому статистичну оцінку позначають . При цьому , а випадкова величина, що має певний закон розподілу ймовірностей.

ТОЧКОВІ СТАТИСТИЧНІ ОЦІНКИ

Означення точкової статистичної оцінки.

Класифікація точкових оцінок.

Статистична оцінка яка визначається одним числом, називається точковою статистичною оцінкою.

Точкова оцінка називається незміщеною якщо її математичне сподівання дорівнює параметру, що оцінюється:

Нехай вибірка з досліджуваної генеральної сукупності з параметром , через позначимо точкову оцінку яка визначається цією вибіркою.

Точкова оцінка називається обгрунтованою якщо вона збігається по ймовірності до оцінюваного параметра тобто: .

Оцінки, які мають властивості незміщеності та обґрунтованості можуть відрізнятися дисперсіями.

Точкова оцінка називається ефективною якщо вона має мінімальну дисперсію.

Теорема

Нехай випадкова величина і нехай проведено незалежних дослідів по її дослідженню і відповідні статистичні дані є .

Тоді:

Незміщеною оцінкою математичного сподівання є вибіркове середнє .

Незміщеною оцінкою дисперсії є виправлена дисперсія

Незміщеною оцінкою центрального моменту 3-го порядку є вибірковий центральний момент третього порядку

Незміщеною оцінкою центрального моменту 4-го порядку є вибірковий центральний момент четвертого порядку

Незміщеною оцінкою коефіцієнта асиметрії

є вибірковий коефіцієнт асиметрії

Незміщеною оцінкою коефіцієнта ексцесу

є вибірковий коефіцієнт ексцесу

Вибірковий коефіцієнт асиметрії використовується для перевірки на симетричність, а також для грубої перевірки на нормальність розподілу.

Він дозволяє відхиляти, але не дозволяє прийняти гіпотезу про нормальність розподілу.

Вибірковий коефіцієнт ексцесу також використовується для грубої перевірки на нормальність розподілу.

Він дозволяє відхиляти, але не дозволяє прийняти гіпотезу про нормальність розподілу.

У випадку коли всі частоти дорівнюють 1, вибіркова середня величина обчислюється за допомогою функції СРЗНАЧ( ) табличного процесора EXCEL. Кількість аргументів не повинна перевищувати 30.

У випадку коли частоти дорівнюють , які не всі дорівнюють 1, вибіркова середня величина обчислюється за допомогою функції СУММПРОИЗВ(Діапазон зміни варіант; Діапазон зміни частот)/СУММ(Діапазон зміни частот) табличного процесора EXCEL.

Виправлена дисперсія обчислюється за допомогою функції ДИСП( ) табличного процесора EXCEL. Кількість аргументів не повинна перевищувати 30.

Вибірковий коефіцієнт асиметрії обчислюється за допомогою функції СКОС( ) табличного процесора EXCEL. Кількість аргументів не повинна перевищувати 30.

Вибірковий коефіцієнт ексцесу обчислюється за допомогою функції ЕКЦЕСС( ) табличного процесора EXCEL. Кількість аргументів не повинна перевищувати 30.

Методи визначення точкових статистичних оцінок

Метод аналогій

Цей метод базується на тому, що для параметрів генеральної сукупності вибирають такі самі параметри вибірки. Наприклад, для оцінок , вибирають, відповідно, , .

Метод максимальної правдоподібності

Метод максимальної правдоподібності для дискретних випадкових величин.

Нехай Х дискретна випадкова величина, яка в результаті n незалежних дослідів приймає значення . Припускається, що вид закону розподілу відомий, але невідомий параметр який входить до нього, тобто .

Ймовірність події яка полягає в тому, що одночасно будуть спостерігатися значення дорівнює (це випливає з теореми про ймовірність добутку незалежних подій).

Чим більше , як функція , тим параметр кращий в тому сенсі, що довіра до набору є більшою, тому функцію називають функцією правдоподібності, для дискретної випадкової величини Х.

Суть методу найбільшої правдоподібності полягає в тому, що за оцінку беруть таке його значення яке дає функції максимум.

Метод найбільшої правдоподібності, запропонований англійським біологом, математиком і статистиком Р. Фішером (1890-1962)

Функцію - називають оцінкою найбільшої правдоподібності.

Оскільки і досягають максимуму при тому ж значенні то на практиці розглядають задачу максимізації , тому що працювати з сумами простіше ніж з добутками.

Логарифм функції правдоподібності називають логарифмічною функцією правдоподібності.

Для розв’язку задачі максимізації треба:

1) розв’язати систему

2) для знайденого розв’язку системи перевірити умову матриця складена з елементів є від’ємно визначеною.

У випадку скалярного параметра наведений алгоритм має особливо простий вигляд: