Властивості множення матриць

1. Некомутативність: добуток двох матриць залежить від порядку множників, тому для більшості випадків .

Проте для деяких пар квадратних матриць А і В може трапитись, що ; такі матриці називаються переставними.

2. Асоціативність: якщо добутки АВ і ВС визначені, то .

3. Дистрибутивність відносно операції додавання матриць:

a) якщо добутки АС і ВС визначені, то ;

b) якщо добутки СА і СВ визначені, то .

4. Дистрибутивність відносно числа: якщо добуток АВ визначений, то для будь-якого числа  виконуються рівності (АВ)=(А)В=А(В).

5. Існує нейтральний елемент відносно множення квадратних матриць. Це одинична матриця того ж порядку, тобто для будь-якої матриці справджуються рівності .

6. Визначник добутку матриць дорівнює добутку визначників цих матриць: .

Матриці, для яких має місце рівність АВ=ВА, називаються переставними.

3.2.3.Транспонування матриць

Крім розглянутих основних операцій над матрицями застосовується ще одна – транспонування – таке перетворення матриці, при якому рядки цієї матриці стають її стовпцями з тими самими номерами.

Сума і добуток матриць та добуток матриці на число транспонуються за такими правилами:

1. Для будь-яких матриць А та В того самого розміру .

2. Якщо добуток АВ матриць А та В визначений, то .

3. Для кожної матриці і будь-якого числа  .

Квадратна матриця А називається симетричною, якщо дорівнює транспонованій до неї матриці, тобто , і кососиметричною, якщо дорівнює транспонованій до неї матриці, яка взята з протилежним знаком, тобто . Причому, довільну квадратну матрицю можна записати у вигляді суми симетричної і кососиметричної матриць, де симетрична матриця знаходиться за формулою , а кососиметрична .

Приклад 3.6. Записати матрицю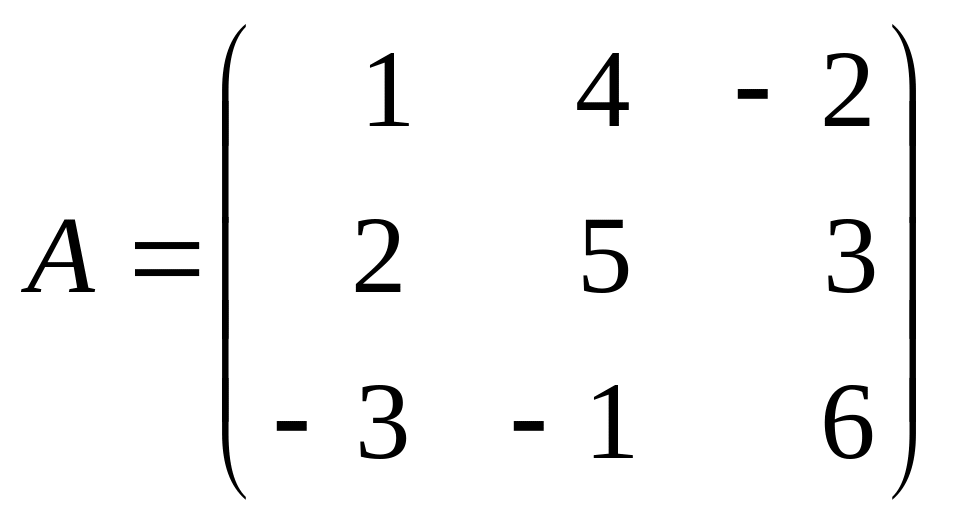 у вигляді суми симетричної і кососиметричної матриці.

 Знайдемо матрицю, транспоновану до даної 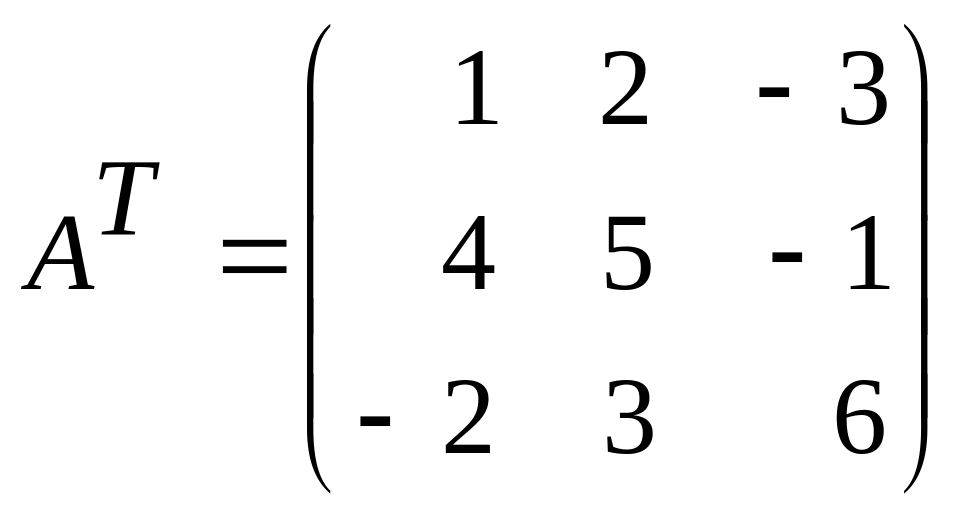, і за вище записаними формулами обчислимо симетричну матрицю і кососиметричну матрицю 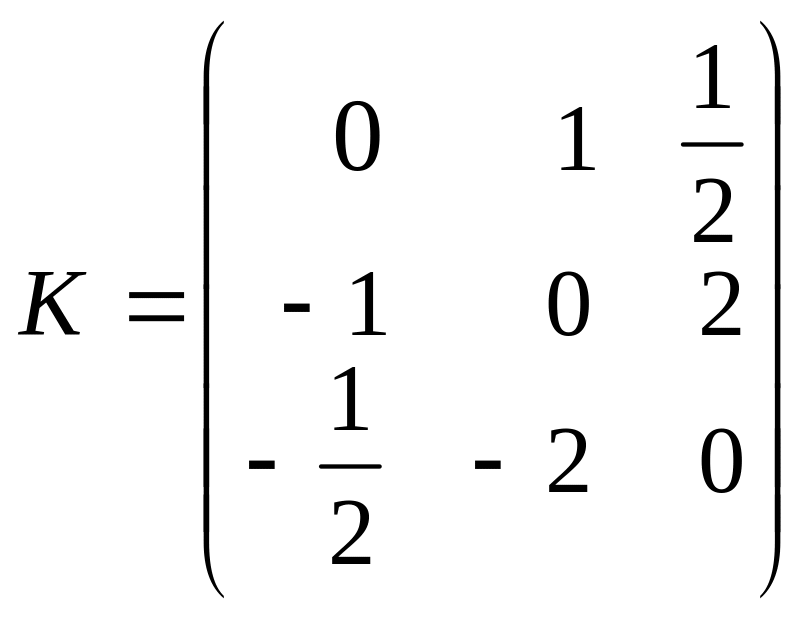. Отже, матриця . 

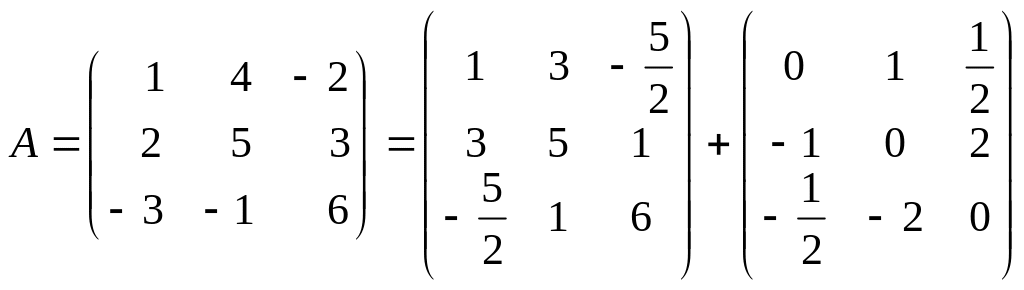3.2.4. Обернена матриця

Матриця називається оберненою до матриці А, якщо . Матриця називається невиродженою (або неособливою), якщо її визначник відмінний від нуля, і виродженою (або особливою), якщо визначник дорівнює нулю.

3.2.4.1. Обчислення оберненої матриці за допомогою алгебраїчних доповнень

Нехай – довільно вибрана матриця n-го порядку. Матриця , в якій елементами i-го рядка є алгебраїчні доповнення елементів i-го стовпця матриці А, називається взаємною матрицею до матриці А, тобто

Щоб отримати цю матрицю , потрібно на місце кожного елемента матриці А поставити його алгебраїчне доповнення і одержану матрицю транспонувати (дія, аналогічна транспонуванню визначника). Тепер обчислимо добутки і . Користуючись формулами (1.8) – (1.11), дістанемо

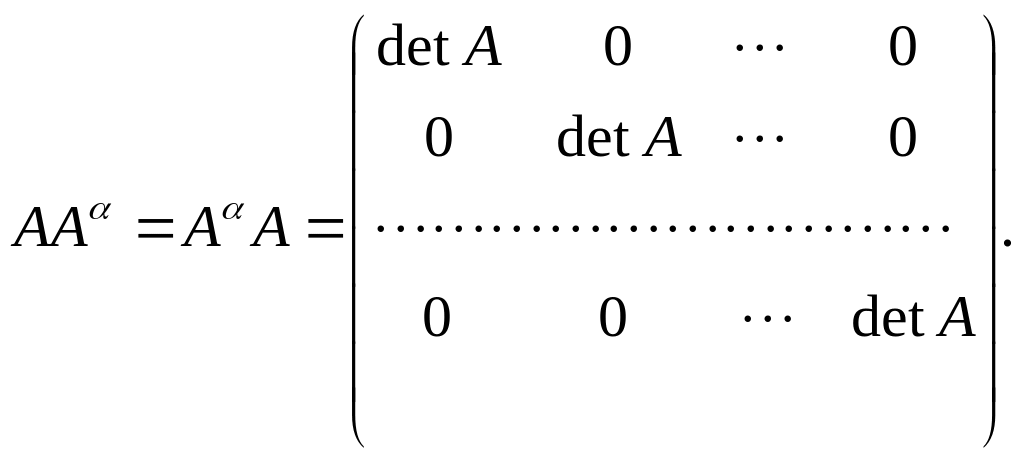(3.7)

Тепер для одержання в формулі (2.7) одиничної матриці необхідно поділити кожен елемент даної матриці на , а цю дію можна виконати лише за умови, що визначник матриці А відмінний від нуля, тобто матриця А є невиродженою.

Теорема 3.2. Для того, щоб існувала матриця, обернена до матриці А, необхідно і достатньо, щоб матриця А була невиродженою.

Отже, виконавши умови теореми 2.2, маємо формулу оберненої матриці:

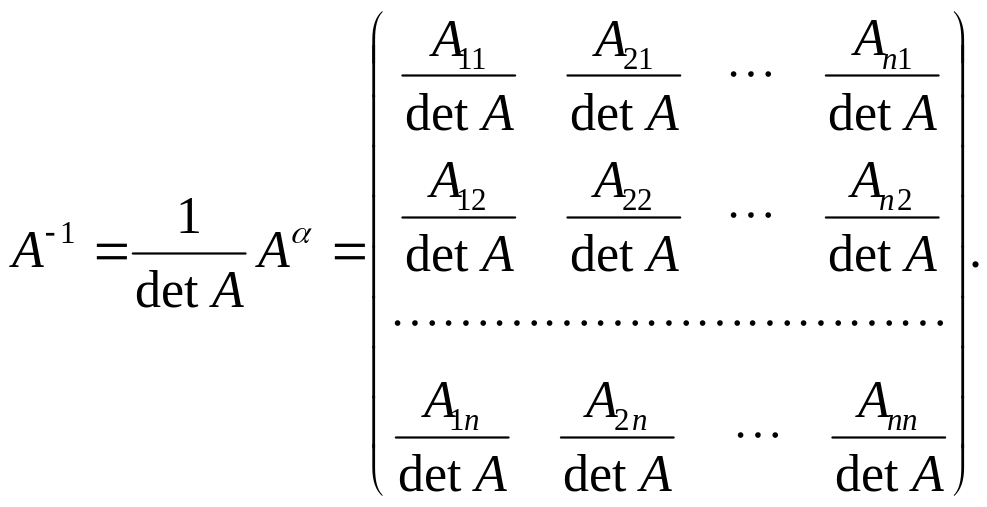(3.8)

Приклад 3.7. Знайти матрицю, обернену до матриці

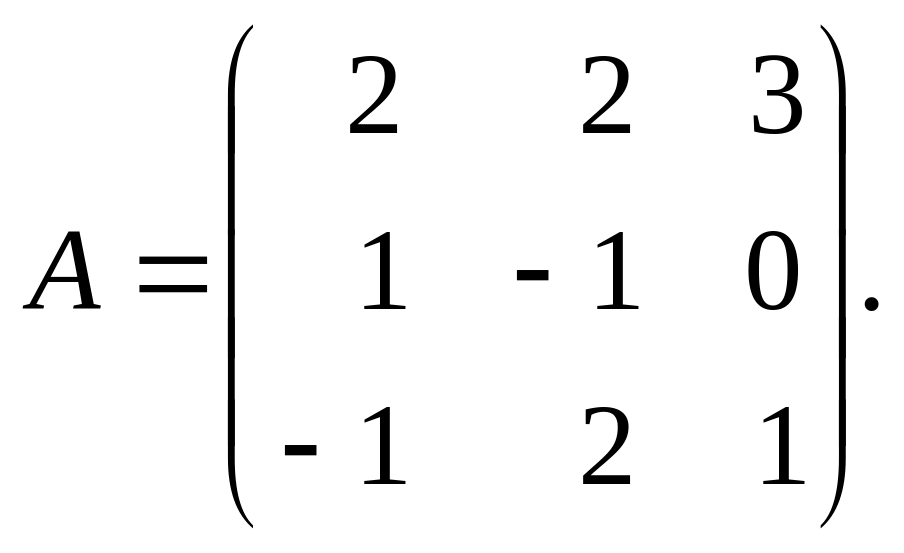
 Обчислимо визначник цієї матриці .

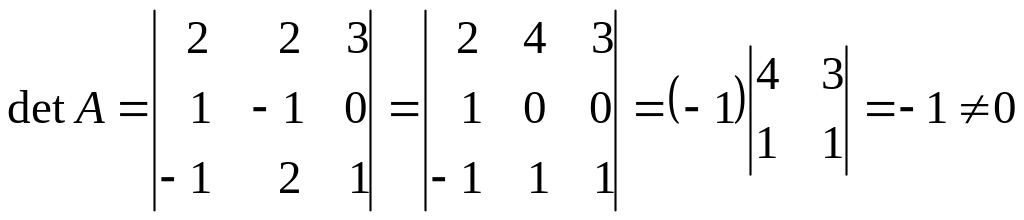Визначник відмінний від нуля, отже, обернена матриця існує. Знайдемо алгебраїчні доповнення всіх елементів матриці А:

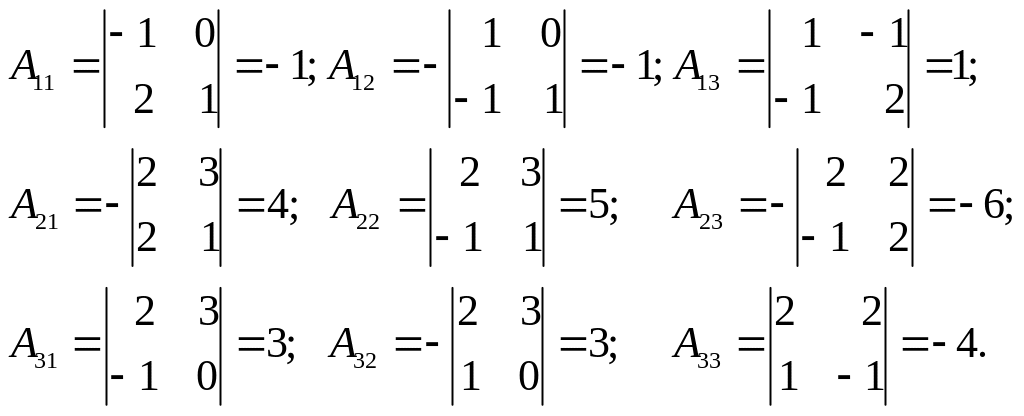
За формулою (3.8) складемо обернену матрицю

