Постройте доверительный интервал для оценки математического ожидания объединенной выборки. Сравнить со значениями, вычисленными в лабораторной работе № 1.

5. Контрольные вопросы

1. Какие выборки называются однородными?

2. Какие значения основных статистических параметров должны иметь однородные выборки?

3. Как выполняется проверка гипотезы о равенстве дисперсий?

4. Как выполняется проверка гипотезы о равенстве математических ожиданий?

5. В каком случае можно объединять две выборки?

ЛАБОРАТОРНАЯ РАБОТА № 5 ОБЪЕДИНЕНИЕ СЕРИЙ НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ /двухвыборочный t-тест для средних/

1. Цель работы

Изучить основные особенности и методы объединения результатов разных серий измерений в общий массив значений.

2. Задание

Выполнить объединение двух выборок разного объема из разных нормальных совокупностей с одинаковым математическим ожиданием и разной дисперсией, используя приближенный двухвыборочный t-критерий.

3. Краткая теория

В предыдущей работе была рассмотрена процедура проверки гипотезы о равенстве средних (математических ожиданий) двух нормальных распределений с неизвестными дисперсиями. При этом делалось предположение о равенстве дисперсий между собой.

Если при анализе результатов измерений была обнаружена неравноточность серий (условие (4.3) работы № 4 не выполнено), то гипотезу о равенстве математических ожиданий можно проверить по приближенному критерию:

, (5.1)

где

. (5.2)

Статистика t в выражении (5.1) подчиняется распределению Беренса-Фишера, пользование которым весьма затруднительно из-за отсутствия нужных таблиц и сложности процедуры пользования имеющимися. Приближенное выражение (5.2) позволяет пользоваться таблицами t-распре­деления.

Если обнаружена неравноточность измерений в сериях, но серии однородны по условию (5.1), при совместной их обработке неравноточность учитывается при расчете среднего арифметического введением весов , а вычисления выполняются по формулам:

(5.3)

где выборочные средние, общее среднее (среднее арифметическое объединенных серий), выборочные оценки дисперсии.

Из курса теории вероятностей известно, что случайная величина в виде суммы двух случайных нормальных величин имеет также нормальное распределение. Однако в данном случае нельзя говорить о сумме случайных величин. Мы имеем дело со смесью двух распределений, нормальных, но с разными параметрами. Закон распределения такой смеси идентифицировать нельзя – он зависит от объемов выборок и от параметров обоих распределений. Чтобы убедиться в этом, можно построить гистограмму для объединенного массива для заметно различающихся объемов выборок, дисперсий или математических ожиданий (последнее наиболее наглядно покажет правильность нашего утверждения).

По этой причине оценивание математического ожидания доверительным интервалом Стьюдента будет весьма приближенным. По этой же причине мы не рекомендуем вычислять оценку СКО для объединенного массива как не имеющую смысла при неизвестном законе распределения. Наконец, по этой же причине в метрологии при объединении неравноточных результатов обычно ограничиваются указанием значения . Можно воспользоваться интервалом Чебышева, хотя скорее всего он будет излишне широким.

Интервал Чебышева – интервал вероятности для случайной величины, распределенной по любому закону, но с конечными математическим ожиданием и дисперсией, имеет вид (в качестве случайной величины используем общее среднее):

Поскольку неизвестна, воспользуемся ее оценкой по последней формуле из (5.3). Задавшись вероятностью, например, 0.90, мы приближенно получим откуда приближенный доверительный интервал Чебышева примет вид:

(5.4)

при доверительной вероятности 0.90 (напомним, что для конкретного численного доверительного интервала следует говорить «при надежности 0.90»).

4. Ход работы

1. Получите n1_i~N(5;4) и n2_i~N(5;1), – две серии случайных чисел, распределенных по нормальному закону, с математическим ожиданием равным 5, и дисперсиями равными 4 и 1 соответственно (для этого выполните шаги п.2, лабораторной работы № 1). Размерность серий может быть произвольной, необязательно одинаковой.

2. Выполните расчет двухвыборочного F-теста для дисперсий, используя одноименный инструмент надстройки Анализ данных (см. рис. 4.1 лаб. работы № 4).

Таблица результатов работы надстройки «Двухвыборочный F-тест для дисперсий» для данной работы представлена на рис. 5.1.

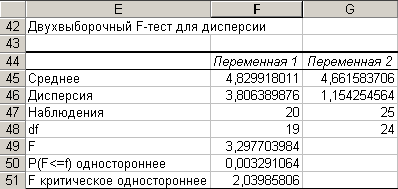
Рис. 5.1. Таблица результатов расчета F-теста

Обратите внимание, что в качестве Интервала переменной1 выбрана серия с большим значением оценки дисперсии, а в качестве Интервала переменной2 – с меньшей.

3. Проверьте гипотезу о равенстве дисперсий в сериях n1 и n2 по таблице значений параметров надстройки «Двухвыборочный F-тест для дисперсий» (рис. 5.1).

Основное описание работы F-теста приведено в лаб. работе № 4.

• По формулам, описанным в предыдущей лаб. работе, получены следующие двусторонние критические значения (см. рис. 5.1) = = 0,407776923 и = 2,345153405. Таким образом, при двусторонней оценке получим критическую область как объединение двух интервалов .

• Однако и в случае двусторонних оценок значение критерия F принадлежит правому критическому интервалу, следовательно, гипотеза не принимается.

4. Сравните расчетное значение F с параметром F критическое одностороннее по формуле (4.3), если F  F_кр., гипотеза также не принимается.

• В случае, если в качестве Интервала переменной1 указана серия с меньшим значением оценки дисперсии, то тогда для расчетного значения F и F критического одностороннего необходимо найти их обратные значения, которые и необходимо сравнивать по формуле (4.3). Для вычисления F критического одностороннего также подходит формула =FРАСПОБР(0,05;G48;F48), где ячейки F48 и G48 содержат значения соответствующего числа степеней свободы выборок.

4. Выполните проверку однородности (гипотезу о равенстве математических ожиданий) серий измерений по таблице значений параметров надстройки «Двухвыборочный t-тест с различными дисперсиями» (рис. 5.2). Значения Среднего (ячейки F60 и G60), Дисперсии (ячейки F61 и G61) рассчитываются с помощью соответствующих функций, описанных в лаб. работе № 1.

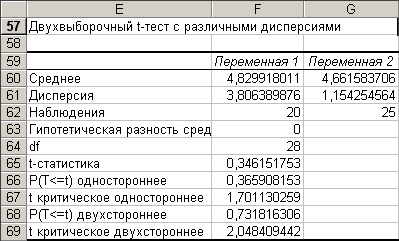
Рис. 5.2. Таблица результатов расчета t-теста

• Число степеней свободы (показатель df) рассчитывается в ячейке F64 по формуле (5.2). В синтаксисе Excel это выражение запишется так:

=((F61/F62+G61/G62)^2/((F61/F62)^2/(F62+1)+(G61/G62)^2/(G62+1))-2)

После этого полученное значение округляется в меньшую сторону функцией ОКРУГЛВНИЗ до целого, для чего вторым аргументом записывается нуль.

• Основной показатель данной надстройки t-статистика вычисляется согласно формуле (5.1). В синтаксисе Excel формула примет следующий вид:

=ABS(F60-G60)/КОРЕНЬ(F61/F62+G61/G62)

Здесь значения функций, применяемых в формуле интуитивно понятны. В случае сомнений см. Справочную систему Excel.

• Модуль значения t критического двустороннего вычисляется в ячейке F69 по формуле =СТЬЮДРАСПОБР(0,05;F64). Сведения по функции СТЬЮДРАСПОБР можно найти в лаб. работе № 2.

• Для расчета значения одностороннего (ячейка F66) и двустороннего (ячейка F68) -значения t-теста можно использовать функцию ТТЕСТ, родственную режиму «Двухвыборочный t-тест с одинаковыми дисперсиями» (рис. 5.2). Сведения по функции ТТЕСТ приведены в лаб. работе № 4.

Для случая различных дисперсий P(T<=t) одностороннее (ячейка F66 рис. 5.2) вычисляется по формуле

=СТЬЮДРАСП(F65;F64;1).

Сравните полученное значение с вычисленным по формуле

=ТТЕСТ(A43:A62;C43:C67;1;3),

для неокругленного числа степеней свободы.

Значение P(T<=t) двустороннего (ячейка F68 рис. 5.2) вычисляется по формуле

=СТЬЮДРАСП(F65;F64;2).

Сравните полученное значение с вычисленным по формуле

=ТТЕСТ(A43:A62;C43:C67;2;3),

для неокругленного числа степеней свободы.

• Сравните значение t-статистики с t критическим односторонним или двусторонним. Для принятия гипотезы значение t-статистики не должно попадать ни в один из критических интервалов . Так как условие (5.1) выполняется, а также значение t-статистики не попадает ни в один критический интервал, то гипотезу о равенстве математических ожиданий принимаем.

4. Для объединения однородных неравноточных серий результатов измерений выполните расчет основных статистически параметров, используя формулы (5.3).

5. Постройте доверительный интервал для оценки математического ожидания объединенной выборки по формуле (5.4). Сравните со значениями, вычисленными в лабораторной работе № 1.

6. Постройте гистограмму частот с равным шагом, как описано в работе 2. Сравните свою гистограмму с гистограммами других студентов, сделайте вывод.

5. Контрольные вопросы

1. В каком случае нельзя объединять две выборки данных?

2. Почему закон распределения объединенного массива неравноточных выборок оказывается отличным от нормального?

3. Какой доверительный интервал для математического ожидания шире – Стьюдента или Чебышева и по какой причине?

4. Предположим, Вы по объединенному массиву проверили гипотезу о нормальности распределения и не отвергли ее. Каким доверительным интервалом для математического ожидания Вы воспользуетесь?

ЛАБОРАТОРНАЯ РАБОТА № 6 ПОСТРОЕНИЕ ЛИНЕЙНОЙ ЭМПИРИЧЕСКОЙ ЗАВИСИМОСТИ ПО ОПЫТНЫМ ДАННЫМ /метод наименьших квадратов/

1. Цель работы

Изучить основные особенности и методы построения линейного прибли­жения экспериментальных данных.

2. Задание

Методом наименьших квадратов построить линейную эмпирическую зависимость по опытным данным. Выполнить проверку адекватности математической модели опытным данным с помощью статистических критериев. Оценить погрешность эмпирической зависимости совместными доверительными F-интервалами.

3. Краткая теория

Метод наименьших квадратов

Одновременные измерения двух или более разнородных физических величин с целью нахождения зависимости между ними называются совместными измерениями [2]. Обычно выполняется измерений, при которых в заданных или точно измеренных значениях аргумента определены значения функции . Задача состоит в том, чтобы по парам ( , ) построить зависимость (эмпирическую), которая была бы несмещенной и эффективной оценкой истинной зависимости, общий вид которой считают известным. Например, известно, что истинная зависимость есть прямая линия, представленная в виде

. (6.1)

Параметры , неизвестны, их следует оценить по опытным данным. Будем считать ошибки измерений случайными с нулевым математическим ожиданием и дисперсией при любом , а также некоррелированными для разных . При этих условиях найти несмещенные и эффективные оценки , параметров , (а следовательно и зависимости (6.1) в целом) можно с помощью метода наименьших квадратов (МНК).

Будем определять оценку функции в виде

, (6.2)

а оценки , искать таким способом, чтобы сумма квадратов отклонений от по всем узлам была минимальной (этот подход называют также принципом Лежандра):

. (6.3)

Это эквивалентно условию , что приводит к уравнениям вида:

(6.4)

Учитывая, что , – некоторые числа, при этом , получаем

(6.5)

Отметим, что если бы мы записали выражение (6.1) в обычном виде , мы вынуждены были бы решать систему уравнений, выражая параметры один через другой и проводя более сложные вычисления. Использование линейной зависимости в виде (6.1) позволило упростить вычисления (что очень важно для более сложных зависимостей) и получить статистически независимые оценки и .

Учитывая это свойство, можно записать:

Переходя к оценкам, получаем:

(6.6)

При любом законе распределения (если удовлетворяются указанные выше условия) несмещенной оценкой (а при нормальном законе распределения и эффективной) является остаточная дисперсия

, (6.7)

где – число коэффициентов регрессии (для прямой линии =2).

Окончательно получаем

, (6.8)

то есть оценка СКО является функцией от . Значение минимально при и увеличивается к началу и к концу интервала значений аргумента.

Статистическая проверка адекватности модели

Все приведенные выше выражения справедливы при выполнении предположения о том, что истинный вид зависимости заранее известен, причем эта зависимость линейна по искомым параметрам. Если же это не так, что обычно и имеет место, то утверждение о несмещенности оценок , параметров , оценки дисперсии и оценки (эмпирической зависимости) неизвестной истинной зависимости становится необоснованным, и правильнее исходить из предположения об их смещенности. Для того, чтобы проверить гипотезу о несмещенности модели (говорят об адекватности модели опытным данным), пользуются статистическими критериями.

Известный F-критерий проверки адекватности модели опытным данным использует статистику в виде отношения остаточной дисперсии (6.7) к независимой несмещенной оценке дисперсии опытных данных , где – число степеней свободы этой оценки:

. (6.9)

На практике исследователь часто не имеет в своем распоряжении независимой несмещенной оценки дисперсии опытных данных и не может воспользоваться критерием (6.9). В этом случае можно воспользоваться следующим критерием:

. (6.10)

Этот критерий использует статистику в виде отношения двух последовательных по числу параметров модели остаточных дисперсий; здесь, как обычно, число степеней свободы . В нашем конкретном случае, когда модель имеет вид прямой линии, остаточная дисперсия (6.7) соответствует (числитель статистики). Для нахождения знаменателя следует перейти к более сложной модели, содержащей не 2, а 3 параметра (параболе второй степени), и найти для нее остаточную дисперсию. Однако этот вопрос выходит за рамки изучаемого курса, поэтому в данной работе предполагается, что имеется независимая несмещенная оценка дисперсии, либо известна сама дисперсия .

Линейному регрессионному анализу посвящено множество работ разной сложности, из которых отметим [6, 12, 13, 14]. Наиболее доступно он изложен в [5, 6].

Оценивание погрешности эмпирической зависимости

Погрешность – это некий интервал, построенный в обе стороны от результата измерений и включающий в себя ("накрывающий") неизвестное истинное значение измеряемой физической величины с высокой вероятностью (с заданной или оцененной). Имея оценку СКО эмпирической зависимости (6.8), можно при каждом значении аргумента вычислить доверительные границы для истинного значения при данном значении аргумента, т.е. построить доверительный t-интервал для истинного значения при данном значении аргумента. Такие доверительные t-интервалы называются индивидуальными t-интервалами. Если повторять опыты (каждый раз с новыми опытными данными в тех же узлах) и следить за любым выбранным узлом, то доля индивидуальных t-интервалов, накрывающих истинное значение в этом узле (любом) будет в точности равна заданной доверительной вероятности. Однако, если мы будем следить за несколькими узлами (например, за всеми), то мы заметим, что доля узлов, в которых накрытие не имеет место в данном опыте, совсем не соответствует этой доверительной вероятности. Доля узлов, в которых накрытие не имеет места, может оказаться весьма значительной. От этого недостатка свободны так называемые совместные доверительные интервалы, которые обеспечивают одновременное накрытие истинных значений во всех узлах с вероятностью не меньше заданной.

Погрешность эмпирической зависимости будем выражать совместными доверительными интервалами [12, 5], например, F-интервалами Шеффе, которые проще всего вычислить (они имеют и более серьезные преимущества по сравнению с другими совместными интервалами). Интервалы Шеффе имеют вид:

, (6.11)

где – критическое значение статистики f для выбранного уровня значимости и с числами степеней свободы (числитель) и (знаменатель).

4. Ход работы

1. Для построения регрессионной прямой по методу наименьших квадратов можно воспользоваться двумя подходами: 1) решить систему линейных алгебраических уравнений, корнями которой будут коэффициенты и уравнения прямой регрессии (6.2); 2) воспользоваться встроенными функциями Microsoft Excel. Опишем оба подхода к решению задачи.

   • Вычислите вспомогательные суммы xi, yi, xi^2, yi*xi (функция СУММ(диапазон_значений) или кнопка на палитре инструментов со знаком 'сигма'), а также подсчитайте количество точек данных (функция СЧЕТ(диапазон_значений)). Составьте матрицу из полученных значений согласно формулам метода наименьших квадратов.

   • Для вычисления корней системы можно 1) найти обратную матрицу (функция МОБР(массив), при том надо помнить следующее, для того чтобы получить матрицу необходимо сначала выделить тот диапазон ячеек, в которых предполагается получить значения элементов обратной матрицы, затем ввести функцию в строке формул, и, наконец, нажать комбинацию клавиш CTRL+SHIFT+ENTER. Если нажать одну клавишу ENTER, то Excel вычислит только первый элемент матрицы. Это относится ко всем функциям массива Excel). Умножить обратную матрицу на столбец свободных членов (функция МУМНОЖ(массив1; массив2). Это также функция массива). В результате получаются коэффициенты прямой. 2) по методу Крамера вычислить определители системы и вспомогательные определители переменных (функция МОПРЕД(матрица) – для получения результата достаточно нажать ENTER). Затем вычислить корни системы – коэффициенты прямой.

2. Для реализации второго подхода нужно применить функцию ЛИНЕЙН, которая рассчитывает статистику для ряда с применением метода наименьших квадратов, для вычисления прямой линии, которая наилучшим образом аппроксимирует имеющиеся данные. Функция возвращает массив, который описывает полученную прямую. Поскольку возвращается массив значений, функция должна задаваться в виде формулы массива. Кроме того, нужно использовать функцию ИНДЕКС, с помощью которой можно выделить нужное значение.

Функция ЛИНЕЙН

Синтаксис:

ЛИНЕЙН(извест_значения_y;извест_значения_x;конст; статист)

Извест_значения_y – это множество значений y, которые уже известны для соотношения (6.2).

Замечания:

• Если массив извест_значения_y имеет один столбец, то каждый столбец массива извест_значения_x интерпретируется как отдельная переменная.

• Если массив извест_значения_y имеет одну строку, то каждая строка массива извест_значения_x интерпретируется как отдельная переменная. Извест_значения_x – это необязательное множество значений x, которые уже известны для соотношения (6.2). Массив извест_значения_x может содержать одно или несколько множеств переменных. Если используется только одна переменная, то извест_значения_y и извест_значения_x могут быть массивами любой формы при условии, что они имеют одинаковую размерность. Если используется более одной переменной, то извест_значения_y должны быть вектором (то есть интервалом высотой в одну строку или шириной в один столбец).

• Если извест_значения_x опущены, то предполагается, что это массив {1;2;3;...} такого же размера как и извест_значения_y.

Конст – это логическое значение, которое указывает, требуется ли, чтобы константа была равна 0.

• Если конст имеет значение ИСТИНА или опущено, то вычисляется обычным образом. Если конст имеет значение ЛОЖЬ, то полагается равным 0.

Статистика – это логическое значение, которое указывает, требуется ли вернуть дополнительную статистику по регрессии.

• Если статистика имеет значение ИСТИНА, то функция ЛИНЕЙН возвращает дополнительную регрессионную статистику, так что возвращаемый массив будет иметь вид: {mn;mn-1;...;m1;b:sen;sen1;...;se1; seb:r2;sey:F;df:ssreg; ssresid}. Если статистика имеет значение ЛОЖЬ или опущена, то функция ЛИНЕЙН возвращает только коэффициенты и постоянную .

Функция ИНДЕКС

Синтаксис:

ИНДЕКС(массив;номер_строки;номер_столбца)

Массив – это интервал ячеек или массив констант. Номер_строки – это номер строки в массиве, из которой нужно возвращать значение. Если номер_строки опущен, то аргумент номер_столбца нужно задавать обязательно. Номер_столбца – это номер столбца в массиве, из которого нужно возвращать значение.

Замечания:

• Если номер_столбца опущен, то аргумент номер_строки нужно задавать обязательно. Если используются оба аргумента номер_строки и номер_столбца, то функция ИНДЕКС возвращает значение, находящееся в ячейке на пересечении номер_строки и номер_столбца.

• Если массив содержит только одну строку или один столбец, то соответствующий аргумент номер_строки или номер_столбца не является обязательным.

• Если массив занимает больше, чем одну строку и больше, чем один столбец, а задан только один аргумент номер_строки или номер_столбца, то функция ИНДЕКС возвращает массив из целой строки или целого столбца аргумента массив.

• Если задать номер_строки или номер_столбца равным 0 (нулю), то функция ИНДЕКС вернет массив значений для целого столбца или целой строки, соответственно. Для того, чтобы использовать значения, возвращаемые как массив, функцию ИНДЕКС нужно ввести как формулу массива в горизонтальный интервал ячеек. Для ввода формулы массива нажмите клавиши CTRL+SHIFT+ENTER.

Таким образом, для вычисления коэффициента в строке формул запишем:

=ИНДЕКС(ЛИНЕЙН(B2: B20;A2:A20);1).

Для вычисления коэффициента –

=ИНДЕКС(ЛИНЕЙН(B2:B20;A2:A20);2).

Полученные по обоим способам значения коэффициентов прямой будут идентичны.

3. Постройте столбец значений регрессионной прямой, вычисленных по формуле (6.2), где х – известные значения аргумента, и – коэффициенты, вычисленные одним из описанных способов.

4. Постройте графики исходной зависимости и МНК-прямой в одних осях (мастер диаграмм).

5. Вычислите значения оценки СКО для МНК-прямой и погрешности х по формуле в точках .

6. Нанесите полученные значения погрешности на тот же график. Для точек МНК-прямой в диалоговом окне Формат рядов данных показать обе планки погрешностей по Х. Сравнить с вычисленными значениями погрешностей.

7. Выполните построение МНК-прямой и вычисление различных статистических параметров с помощью категорией «Регрессия» Пакета анализа Excel. Сравните полученные результаты с результатами предыдущих пунктов работы.

5. Контрольные вопросы

1. В чем суть метода наименьших квадратов построения линейной эмпирической зависимости? Сформулируйте принцип Лежандра.

2. Что такое остаточная дисперсия? Каковы статистические характеристики остаточной дисперсии при нормальном законе распределения?

3. Какие статистические критерии используются для проверки адекватности модели опытным данным при наличии и отсутствии независимой несмещенной оценки дисперсии?

4. Что такое погрешность? Как определить погрешность эмпирической зависимости?

ЛАБОРАТОРНАЯ РАБОТА № 7 ОЦЕНКА СВЯЗИ НОМИНАЛЬНЫХ ПРИЗНАКОВ /таблицы сопряженности/

1. Цель работы

Освоить элементарные приемы анализа таблиц сопряженности 22, в которых представлены результаты наблюдений в номинальных шкалах, с целью оценки связи номинальных признаков.

2. Задание

Создать с помощью генератора случайных чисел 4 случайных двухзначных числа из равномерной совокупности и представить их в виде таблицы 22 для некоторых условных признаков Проверить гипотезу о независимости признаков, вычислить коэффициент связи

3. Краткая теория

Начнем с примера. В приведенной ниже табл. 1 представлены сведения о числе людей, заболевших и не заболевших холерой с указанием, была ли им сделана противохолерная прививка (пример взят из [11]).

Таблица 1

	Незаболевшие	Заболевшие	Всего
Привитые	1625	5	1630
Непривитые	1022	11	1033
Всего	2647	16	2663

Задача состоит в том, чтобы выяснить, эффективна ли прививка, значимо ли ее влияние на вероятность заболевания. Видно, что доля заболевших среди непривитых больше, чем среди привитых, но не объясняется ли это случайными факторами? Аналогичных примеров можно привести множество – это и обработка анкет разного рода, исследований социологического, медицинского, экономического характера, иначе говоря – данных, представленных в номинальных шкалах (вместо числового значения указывается то или иное имя). Если градация признаков и групп (будем называть признаками «имена», указанные в крайнем левом столбце, а группами – указанные в верхней стоке) осуществлена по принципу «да – нет», причем суммы по нижней строке и правому столбцу совпадают, то такая таблица называется таблицей сопряженности (признаков) 22. Отметим, что существуют таблицы сопряженности размером , если группы и признаки разбиты на подгруппы и уровни. Мы ограничимся статистическим анализом таблицы сопряженности 22. Ознакомиться подробнее с таблицами сопряженности и их обработкой можно по [11].

В качестве нулевой гипотезы примем утверждение: прививка не оказывает заметного влияния на вероятность заболевания, а видимый эффект есть следствие случайных вариаций числа заболевших. На языке математической статистики это звучит так: вероятность заболевания для привитых и непривитых равна одному и тому же значению Иначе можно записать так:

Замечание: Мы сильно осложнили бы свою задачу, если бы в качестве нулевой гипотезы выдвинули противоположное утверждение о значимости влияния прививки, т.к. такая гипотеза оказывается множественной (нам пришлось бы указывать, насколько сильно влияние прививки, во сколько раз или на сколько она снижает вероятность заболевания).

Но вероятность остается нам неизвестной, значит надо воспользоваться ее оценкой. По теореме о сходимости (по вероятности) относительной частоты события к его вероятности такой оценкой является средняя относительная частота заболевания по всей исследуемой выборке (по обеим группам): Соответственно, вероятность не заболеть приблизительно равна Таким образом, нам следует сравнить полученные в опыте частоты ( ) с теоретическими, вычисленными в предположении, что гипотеза справедлива. Это проще всего сделать с помощью известного из курса теории вероятностей и математической статистики критерия . Отметим, что это приближенный критерий, существуют и другие, более точные критерии, но они более сложны. Составим новую таблицу, в которой наряду с наблюдаемыми частотами (верхнее число в каждой ячейке) укажем также ожидаемые в предположении справедливости нулевой гипотезы частоты, равные произведению общего числа наблюдений на соответствующие вероятности или (они указаны во второй строке ячеек в круглых скобках). В третьей строке каждой ячейки укажем разность между наблюдаемыми и теоретическими частотами (в квадратных скобках).

Таблица 2

Привитые	1625 (1620.21) [4.79]	5 (9.79) [-4.79]
Непривитые	1022 (1026.79) [-4.79]	11 (6.21) [4.79]

Критерий согласия имеет вид:

, (7.1)

где – верхний -предел статистики , а число степеней свободы, как обычно, равно общему числу слагаемых минус 1 и минус число уравнений связи

(7.2)

Общее число слагаемых (мы имеем двойную сумму) равно 4, а число уравнений связи равно 2 (сумма по строкам равна сумме по столбцам и равна ), т.е. Обратите внимание на то, что разности между частотами в каждой ячейке равны по модулю, т.е. чтобы найти их нужно сделать лишь одно вычисление.

Найдем наблюденное значение статистики критерия:

По таблице процентных точек распределения путем интерполяции найдем приближенное значение :

• уровню значимости 2.5 % соответствует предел ;

• уровню значимости 1 % соответствует предел .

Следовательно, значение 6.07 соответствует уровню значимо­сти

Это и есть «уровень значимости нулевой гипотезы», он слишком мал, чтобы считать гипотезу верной. Опыт вынуждает нас отклонить гипотезу о том, что прививка не оказывает влияния на вероятность заболевания, и мы приходим к выводу, что прививка заметно уменьшает эту вероятность.

4. Ход работы

1. Создайте таблицу сопряженности размерностью 22. Для этого вспомните ситуацию из личного опыта о наличии (отсутствии) некоторого признака у двух групп людей (социологическое исследование). Ситуация должны быть типа «да-нет», т.е. в первой строке предполагается наличие признака, во второй – его отсутствие (см. табл. 1).

   • Укажите названия признаков в первом столбце таблицы и названия групп в верхней строке (если затрудняетесь, то в качестве имен укажите числительные «первая», «вторая»).

   • Выполните генерацию случайных чисел, распределенных по равномерному закону (см. лаб. работу № 1). Каждое полученное число умножьте на 1000 и округлите до целого (подумайте почему?)

   • Найдите суммы полученных значений по строкам, столбцам и общую сумму.

2. В отдельной таблице рассчитайте теоретические частоты для выбранной гипотезы по формуле , где – сумма значений по строке; – сумма значений по столбцу; – общая сумма (общее число наблюдений). Пользуйтесь абсолютными ссылками!

   • Для контроля значений теоретических частот вычислите суммы. Они должны совпадать с вычисленными в исходной таблице.

3. Вычислите значение статистики по формуле (7.1). При необходимости сформируйте вспомогательную таблицу значений выражения под знаком суммы.

4. По таблице процентных точек распределения определите уровень значимости . Вычислите критическое значение с помощью функции Excel ХИ2РАСП(х;Степени_свободы) (см. лаб. раб. № 3 «Проверка нормальности…»). Сделайте вывод о принятии гипотезы .

5. Контрольные вопросы

1. Какие признаки называются номинальными?

2. В каких случаях используются таблицы сопряженности признаков?

3. Какую гипотезу и почему выдвигают при обработке таблиц сопряженности?

4. На основании чего делается вывод о зависимости признаков?

Заключение

В пособии рассмотрены лишь 7 задач по обработке данных, но эти задачи являются основными и на их базе строится дальнейший, более глубокий анализ результатов измерений и наблюдений. Приведенные в них теоретические сведения довольно кратки, но их достаточно для понимания того, какие именно операции выполняет или должен выполнить компьютер. В любом случае студенту на этапе освоения пакета электронных таблиц MS Excel в части применения его к решению описанных задач, рекомендуется внимательно ознакомиться с прил. 1–3, в которых отмечены как тонкости процедур диалога с компьютером, так и типичные ошибки операторов. Полезно также контролировать правильность действий и получаемые результаты с помощью отдельных контрольных операций с использованием статистических таблиц, приведенных в прил. 4.

Отметим в заключение, что хотя пакет Excel не является наилучшим статистическим пакетом, его широкое распространение в различных сферах человеческой деятельности послужили толчком к составлению данного сборника.

«Цель вычислений – понимание, а не числа» (Р. Хэмминг).

Приложение 1 Установка надстройки "Пакет анализа"

Для того, чтобы отыскать команду вызова надстройки Пакет анализа в Microsoft Excel, необходимо воспользоваться меню Сервис (рис. 1).

Здесь возможны следующие ситуации:

1. В меню Сервис присутствует команда Анализ данных… (рис. 1). Это самый простой и идеальный случай, так как достаточно щелкнуть указателем мыши, чтобы воспользоваться окном надстройки.

2. В меню Сервис отсутствует команда Анализ данных… В этом случае необходимо в том же меню выполнить команду Надстройки… В результате раскроется одноименное диалоговое окно со списком доступных надстроек (рис. 2). Среди доступных надстроек выберите элемент Пакет анализа. После этого в меню Сервис появится соответствующая команда. Эта ситуация наиболее типична, так как надстройка Пакет анализа инсталлируется при стандартной установке.

3. В меню Сервис отсутствует команда Анализ данных…, а в списке окна Надстройки нет элемента Пакет анализа. Это самая сложная ситуация, так как без установочного комплекта MS Office не обойтись. После установки дистрибутивного компакт-диска Microsoft Office, перейдите в папку Панель управления (главное меню Пуск) – Установка и удаление программ (рис. 3). Выберите кнопку Заменить, затем следуйте инструкциям Мастера установки, выбирая те пункты и опции, которые вам необходимы. При установки надстройки Пакет анализа установите и все другие надстройки Microsoft Excel. Они значительно расширят возможности программы, а при этом займут на винчестере совсем немного места. Вид диалогового окна Установка и удаление программ может отличаться в разных операционных системах.

Окончание прил. 1

Рис. 3. Диалоговое окно Установка и удаление программ

Если все сделано правильно и названия папок были оставлены по умолчанию, то в папке C:\ Program Files\ Microsoft Office\ Of­fice\ Library\ Analysis появится файл надстройки analysis32.xll.

Приложение 2 Виды ошибок при задании формул

Формула представляет собой синтаксическую конструкцию со знаком “=” в первой позиции, набирается с клавиатуры или кнопкой   Изменить формулу. По этому признаку Excel запускает Палитру формул, которая проверяет синтаксис, автоматически исправляет распространенные ошибки и обеспечивает справочными сведениями.

Формула может содержать следующие элементы:

Выражение – это операнды, соединенные знаками операций. Используемые в формулах Excel операции приведены в таблице 1. Порядок вычисления выражений слева направо с учетом приоритетов операций и может быть изменен скобками ( ).

Таблица 1

Операции в формулах Excel

Операнд – это константа, ссылка на ячейку или диапазон ячеек, заголовок, имя или функция.

Константа – это число или текст, введенные с клавиатуры, в отличие от формулы или возвращаемого ею значения.

Ссылка на ячейку – это адрес ячейки, однозначно определяющий ее месторасположение, в Excel по умолчанию используется стиль адресации А1 по букве столбца и номеру строки, на пересечении которых расположена ячейка. При помощи ссылок можно использовать в одной формуле данные из разных частей листа, а также использовать в нескольких формулах значение одной ячейки.

При создании формул используются следующие типы ссылок.

Абсолютная ссылка – фиксированный адрес ячейки на листе, например, $А$3. Абсолютные адреса предваряются знаком $.

Относительная ссылка – относительно ячейки с формулой, содержащей эту ссылку, например, A3.

Продолжение прил. 2

Смешанная ссылка. Например, А$1 – абсолютная ссылка на первую строку, $A1 – абсолютная ссылка на первый столбец.

Ссылки на ячейки других листов той же книги, Лист2!А1.

Внешние ссылки на другие книги, [Книга2]Лист1!A1 на открытую книгу, иначе с полным путем к книге на локальном диске, ‘С:\Мои документы\[Книга2]Лист1’!$A$1.

Удаленные ссылки на данные других приложений; сетевые адреса и URL (Uniform Resource Locator, унифицированный указатель ресурса, адреса интернета).

Трехмерные ссылки на несколько листов, Лист2:Лист13!A1.

Циклические ссылки – это последовательность ссылок, при которой формула ссылается на себя напрямую или через другие ссылки. Вычисление следующих значений по предыдущим в таких замкнутых последовательностях называется итерацией. Excel прекращает итерационный процесс по заранее установленным ограничениям на количество итераций, по умолчанию 100, или на невязку (разность значений с двух соседних итераций), по умолчанию 0,001.

Ячейки, на которые есть ссылки в указанной ячейке, называются влияющими. Ячейки, в которых есть ссылки на указанную ячейку, называются зависимыми.

При перемещении ячейки, ее формула не изменяется. При этом во всех зависимых ячейках ссылки всех типов выправляются на новое местоположение перемещенной ячейки.

При копировании формулы абсолютные ссылки не обновляются. Относительные ссылки при копировании формулы в другую ячейку обновляются автоматически так, что взаимное расположение влияющих ячеек и формулы сохраняется. Например, формула в ячейке A3 =$A$1+A2 после копирования в ячейку В3 =$A$1+B2. Копирование формулы в примыкающий диапазон можно быстро осуществить протаскиванием маркера заполнения.

Диапазон – это несколько ячеек листа. Ссылка на непрерывный прямоугольный диапазон задается как адрес левой верхней ячейки : адрес правой нижней ячейки. В ссылке на несмежный диапазон поддиапазоны перечисляются через ; и выделяются на листе с нажатым Ctrl.

Формула может содержать одну или несколько функций, связанных между собой арифметическими операторами или вложенных друг в друга. Функции – это встроенные в программу Excel формулы, которые выполняют вычисления по своим аргументам. Обращение к функции идет по имени функции и в скобках списку аргументов через запятую. Вставку функции можно выполнить, используя меню Вставка – Функция… либо одноименную кнопку на панели инструментов Стандартная. В результате будет запущен двухшаговый Мастер функций, содержащий всю коллекцию функций Excel в более чем 10 различных категорий.

Продолжение прил. 2

Аргумент функции – это число, текст, логическая величина, массив, значение ошибки, ссылка, формула или функция. Тип аргумента должен соответствовать типу в описании функции.

Если при задании формулы были допущены ошибки, результатом ее вычисления будет так называемое значение ошибки.

Ошибка #####

Причины возникновения ошибки

1. Введенное числовое значение или результат работы функции не умещается в ячейке.

Меры по устранению ошибки – увеличьте ширину столбца путем перемещения границы, расположенной между заголовками столбцов. Кроме того, можно изменить формат числа ячейки (меню Формат – Ячейки…, вкладка Число).

2. При работе с датами получается отрицательное значение.

Меры по устранению ошибки – введите правильную формулу.

Ошибка #ЗНАЧ!

Причины возникновения ошибки

1. Вместо числового или логического значения введен текст.

Меры по устранению ошибки – проверьте в формуле правильность задания типов аргументов.

2. После ввода или редактирования формулы массива нажимается клавиша Enter.

Меры по устранению ошибки – для редактирования формулы укажите ячейку или диапазон ячеек, содержащих формулу массива, нажмите клавишу F2, а затем – комбинацию клавиш Ctrl+Shift+Enter.

3. Использована неправильная размерность матрицы данных в одной из матричных функций.

Меры по устранению ошибки – укажите правильную размерность при работе с матрицами данных.

Ошибка #ДЕЛ/0!

Причины возникновения ошибки

1. В качестве делителя используется ссылка на ячейку, содержащую нулевое или пустое значение (если аргумент является пустой ячейкой, то ее содержимое интерпретируется как нуль). Такая ситуация чаще всего возникает случайно.

Меры по устранению ошибки – измените ссылку или введите ненулевое значение в ячейку, используемую в качестве делителя.

Продолжение прил. 2

Ошибка #ИМЯ?

Причины возникновения ошибки

1. Используемое в формуле имя было удалено или не определено.

Меры по устранению ошибки – определите имя. Для этого выполните команду Имя меню Вставка

2. Имеется ошибка в написании имени функции.

Меры по устранению ошибки – исправьте написание имени функции вручную или вставьте функцию с помощью мастера функций.

3. В формулу введен текст, не заключенный в двойные кавычки. Excel пытается распознать такой текст как имя, хотя это не предполагается.

Меры по устранению ошибки – заключите текст формулы в двойные кавычки. Например, ессли в ячейке А1 содержится значение 200, я в ячейке В1 – формула = «Итого:»&А1, то в ячейке В1 будет выведен результат Итого:200.

4. В ссылке на диапазон ячеек пропущен знак двоеточия (:).

Меры по устранению ошибки – исправьте формулу так, чтобы во всех ссылках на диапазон ячеек использовался знак двоеточия, например =СУММА(А1:С10).

Ошибка #Н/Д

Причины возникновения ошибки

1. В формуле массива используется аргумент, не соответствующий размеру диапазона, определяющегося числом строк и столбцов.

Меры по устранению ошибки – если формула массива введена в несколько ячеек, проверьте диапазон ссылок формулы на соответствие числу строк и столбцов или введите формулу массива в недостающие ячейки.

2. Не заданы один или несколько аргументов стандартной или пользовательской функции листа.

Меры по устранению ошибки – задайте все необходимые аргументы функции.

3. Используется пользовательская функция, обращение к которой приводит к ошибке.

Меры по устранению ошибки – проверьте, что книга, использующая функцию листа, открыта, и убедитесь в правильности работы функции (проведите отладку в программной среде VBA).

Ошибка #ССЫЛКА!

Причины возникновения ошибки

1. Ячейки, на которые ссылаются формулы, были удалены или в эти ячейки было помещено содержимое других скопированных ячеек.

Окончание прил. 2

Меры по устранению ошибки – измените формулы или сразу же после удаления или вставки скопированного восстановите прежнее содержимое ячеек с помощью кнопки Отменить.

Ошибка #ЧИСЛО!

Причины возникновения ошибки

1. В функции с числовым аргументом используется неприемлемый аргумент.

Меры по устранению ошибки – проверьте правильность использования в функции аргументов.

2. Задана функция, при вычислении которой используется итерационны процесс. При этом итерационный процесс не сходится и результат не может быть получен.

Меры по устранению ошибки – используйте другое начальное приближение для этой функции.

3. Введена формула, рассчитывающая числовое значение, которое слишком велико или слишком мало, чтобы его можно было представить в Microsoft Excel.

Меры по устранению ошибки – измените формулу так, чтобы в результате ее вычисления получалось число, попадающее в диапазон от -110³⁰⁷ до 110³⁰⁷.

Ошибка #ПУСТО!

Причины возникновения ошибки

1. Использован оператор, задающий пересечение диапазонов, не имеющих общих ячеек.

Меры по устранению ошибки – задайте правильно размерность пересекающихся диапазонов или не используйте оператор пересечения, если диапазоны не являются таковыми. В Microsoft Excel оператором пересечения диапазонов является пробел ( ).

Приложение 3 Кратка теория диаграмм

Диаграммы являются средством визуального анализа данных. В любой современной системе программирования есть подобные графические чарты (chart – диаграмма). В табл. 1 приведены основные параметры диаграмм Excel 2000/XP.

Таблица 1

Технические характеристики Excel-диаграмм

Excel предоставляет пользователю 14 стандартных типов диаграмм: гистограмма, линейчатая, график, круговая, точечная, с областями, кольцевая, лепестковая, поверхность, пузырьковая, биржевая и другие. Каждый стандартный тип имеет несколько разновидностей. Постоянно наращивается палитра встроенных нестандартных типов. Коллекция типов диаграмм доступна из меню Диаграмма – Тип диаграммы. Инженерные приложения используют следующие типы диаграмм:

-  график отображает значения однозначной функции y(х) с равными промежутками по аргументу x.

- точечный график строит график функции по точкам (x,y) без ограничений на вид функции.

- сглаженные линии на Графике и Точечной диаграмме соединяют точки плавной кривой.

- поверхность – это график трехмерной поверхности z(x,y).

- контурная поверхность, проекция трехмерной поверхности на координатную плоскость XY в виде карты изолиний z(x,y) = Const.

Организация данных в диаграммах описывается следующей терминологией.

Диаграмма – графический объект на листе Excel. Активная диаграмма запускает в верхнем меню пункт Диаграмма, а также меню Вид и Формат настраиваются для работы с конкретной диаграммой.

Продолжение прил. 3

Элементы диаграммы – отдельные объекты, составляющие диаграмму, довольно разнородные и отличаются для разных типов диаграмм. Элементы активной диаграммы собраны в список на панели инструментов Диаграммы. Все элементы диаграмм оснащены всплывающими подсказками.

Область диаграммы – прямоугольная область, охватывающая все элементы диаграммы. Область построения на плоских диаграммах – это ограниченный координатными осями прямоугольник, содержащий ряды данных. На объемных диаграммах – охватывает три координатные оси со всеми подписями.

Заголовок диаграммы – надпись с описательным текстом. По умолчанию располагается по центру над областью построения.

Ряд данных – группа связанных данных диаграммы. Например, ряд данных для графика составляет диапазон значений функции. На одной диаграмме можно изобразить несколько рядов данных, каждый своим цветом. В качестве имен рядов данных Excel использует заголовки столбцов (или строк) диапазона данных. Если автоматическое распознавание имен рядов прошло безуспешно, Excel сгенерирует имена рядов по умолчанию: Ряд1, Ряд2, Ряд3,.. Имена рядов выводятся в легенду. Точка данных обозначается на диаграмме маркером – это точка, маркер, столбик, сегмент или другой графический примитив, например, на гистограмме это цветной столбик, на графике – квадратик в 5 пунктов.

Легенда. Подпись с условными обозначениями цвета/закраски рядов данных. Легенда обычно располагается справа от области построения. Ключ легенды – условное обозначение в легенде слева от имени ряда, назначенное этому ряду.

Категории – это значения независимой переменной, от которой зависят значения рядов данных, обычно откладываются на горизонтальной оси. Например, на графике значения категорий – это значения аргумента функции. Имена категорий используются для подписей делений оси категорий. Excel пытается распознать заголовки строк (или столбцов) данных для использования их в качестве имен категорий по отличающемуся форматированию первого столбца, иначе автоматически нумерует категории 1, 2, 3,.. В противном необходимо вручную указать адреса ячеек с именами категорий.

Оси – это линии, используемые как основа измерений для построения данных на диаграмме. Ось категорий обычно отображается по горизонтальной оси, например, на графике соответствует оси X, оси независимой переменной. Ось значений – это обычно вертикальная ось, ось Y. Например, на графике значение точки данных изображает расстояние от маркера точки по вертикали до оси категорий в выбранных единицах измерения. Деления и подписи делений осей – это короткие насечки на оси через одинаковые расстояния, их подписи показывают откладываемую по оси меру, а также могут обозначать категории или ряды. Линии сетки – параллельные осям линии, облегчающие просмотр данных на диаграмме.

Окончание прил. 3

Подписи значений отображают дополнительные сведения: значения в отдельных точках, названия категорий, рядов или их комбинации.

К элементам диаграмм также относятся заголовки осей, линии проекции, вспомогательные оси, линии рядов, тренды, коридоры колебания, полосы повышения и понижения, планки погрешности и другие.

В табл. 2 приведены способы создания диаграммы в Excel. Рекомендуется использовать последний способ. Четырехшаговый мастер диаграмм выпытает у вас все параметры диаграммы и создаст с первого раза близкий к желаемому результат.

Таблица 2

Способы создания диаграммы

Размещенная на отдельном листе книги или внедренная в текущий лист диаграмма связана с данными, на основе которых она создана, и обновляется автоматически при их изменении.

Приложение 4 Статистические таблицы

Приведены краткие выдержки из таблиц математической статистики, необходимые и достаточные для выполнения упражнений, приведенных в сборнике. Более точные таблицы см. в [9].

Таблица 1

Интегральная функция нормированного нормального распределения

; ;

В первом столбце и в верхней строке указаны значения аргумента.

Продолжение прил. 4

Таблица 2

Дифференциальная функция нормированного нормального распределения (плотность вероятности)

; ;

Продолжение прил. 4

Таблица 3

Коэффициенты Стьюдента (двухсторонние границы t-распределения)

Таблица 4

Критические значения для наибольшего отклонения эмпирической функции распределения от теоретической (критерий Колмогорова).

Значения , удовлетворяющие условию

Для используют аппроксимации:

.

Продолжение прил. 4

Таблица 5

Распределение (процентные точки). Значения , удовлетворяющие условию или эквивалентному условию

Для построения двухстороннего интервала вероятности для случайной величины, имеющей ‑распределение, удовлетворяю­щего условию , следует учесть, что

Верхнюю границу такого интервала находят по таблице для , а нижнюю – для .

Продолжение прил. 4

Таблица 6

Значения для = 0.05 (верхние 5‑процентные критические значения, односторонний критерий)

Значения для = 0.10 (верхние 10‑процентные критические значения, односторонний критерий)

Окончание прил. 4

Полезные соотношения:

; ,

где – -процентная точка t-распределения, соответствующая вероятности или коэффициент Стьюдента (двухсторонняя граница t-распределения, табл. 3).

Список литературы

1. Макарова Н.В. Статистика в Excel: Учебное пособие/ Макарова Н.В., Трофимец В.Я. – М.: Финансы и статистика, 2002. – 368 с.

2. Селиванов М. Н. Качество измерений / Селиванов М.Н., Фридман А.Э., Кудряшева Т.Ф. – Л.: Лениздат, 1987.

3. Новицкий П. В. Оценка погрешностей результатов измерений / Новицкий П.В., Зограф И.А. – Л.: Энергоатомиздат, 1985.

4. Гмурман В.Е. Теория вероятностей и математическая статистика/ Гмурман В.Е. – М.: Высшая школа, 1997.

5. Чашкин Ю.Р. Статистика для инженеров. Основы регрессионного анализа/ Чашкин Ю.Р. – Хабаровск: Изд-во ДВГУПС, 2003. – 162 с.

6. Худсон Д. Статистика для физиков / Худсон Д. – М.: Мир, 1970.

7. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. Пособие для студентов вузов. Изд. 5-е, стер/ Гмурман В.Е. – М.: Высш. шк., 1999.

8. Чашкин Ю.Р. Математическая статистика. Статистическая обработка результатов измерений. Уч.-метод. пособие для самостоят. работ студентов / Чашкин Ю.Р. – Хабаровск: Изд-во ДВГУПС, 1999.

9. Большев Л.Н. Таблицы математической статистики / Большев Л.Н., Смирнов Н.В. – М.: Наука, 1983.

10. Тюрин Ю.Н. Статистический анализ данных на компьютере / Тюрин Ю.Н., Макаров А.А. Под ред. В.Э.Фигурнова – М.: ИНФРА-М, 1998.

11. Справочник по прикладной статистике. – В 2-ч т. – Т.1: Пер. с англ. / Под ред. Э. Ллойда, У.Ледермана, Ю.Н.Тюрина. – М.: Финансы и статистика, 1989. –370с.

12. Себер Дж. Линейный регрессионный анализ / Себер Дж. – М.: Мир, 1980.

13. Вучков И. Прикладной линейный регрессионный анализ / Вучков И., Бояджиева Л., Солаков Е. –М.: Финансы и статистика, 1987.

14. Дрейдер Н. Прикладной регрессионный анализ. В 2-х кн. Пер. с англ. – 2-е изд., перераб.и доп. / Дрейдер Н., Смит Г. – М.: Финансы и статистика, 1987.

15. Вихтенко Э. М. Численные методы на ЭВМ/ Вихтенко Э.М., Коломийцева С.В., Комова О.С. – Хабаровск: ДВГУПС, 2003. –71с.

Оглавление

ВВЕДЕНИЕ 3

ЛАБОРАТОРНАЯ РАБОТА № 1 ПЕРВИЧНАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ПРЯМЫХ МНОГОКРАТНЫХ ИЗМЕРЕНИЙ /вычисление основных статистических параметров/ 4

1. Цель работы 4

2. Задание 4

3. Краткая теория 4

4. Ход работы 7

5. Контрольные вопросы 12

ЛАБОРАТОРНАЯ РАБОТА № 2 ПОСТРОЕНИЕ ГИСТОГРАММЫ ПО РЕЗУЛЬТАТАМ ПРЯМЫХ МНОГОКРАТНЫХ ИЗМЕРЕНИЙ /на примере результатов математического эксперимента/ 13

1. Цель работы 13

2. Задание 13

3. Краткая теория 13

4. Ход работы 16

5. Контрольные вопросы 20

ЛАБОРАТОРНАЯ РАБОТА № 3 ПРОВЕРКА НОРМАЛЬНОСТИ ЗАКОНА РАСПРЕДЕЛЕНИЯ /тремя различными методами/ 20

1. Цель работы 20

2. Задание 20

3. Краткая теория 20

4. Ход работы 24

5. Контрольные вопросы 28

ЛАБОРАТОРНАЯ РАБОТА № 4 ОБЪЕДИНЕНИЕ РАВНОТОЧНЫХ СЕРИЙ ИЗМЕРЕНИЙ /двухвыборочный t-тест для средних/ 28

1. Цель работы 28

2. Задание 28

3. Краткая теория 28

4. Ход работы 30

5. Контрольные вопросы 36

ЛАБОРАТОРНАЯ РАБОТА № 5 ОБЪЕДИНЕНИЕ СЕРИЙ НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ /двухвыборочный t-тест для средних/ 37

1. Цель работы 37

2. Задание 37

3. Краткая теория 37

4. Ход работы 39

5. Контрольные вопросы 42

ЛАБОРАТОРНАЯ РАБОТА № 6 ПОСТРОЕНИЕ ЛИНЕЙНОЙ ЭМПИРИЧЕСКОЙ ЗАВИСИМОСТИ ПО ОПЫТНЫМ ДАННЫМ /метод наименьших квадратов/ 42

1. Цель работы 42

2. Задание 42

3. Краткая теория 42

4. Ход работы 46

5. Контрольные вопросы 49

ЛАБОРАТОРНАЯ РАБОТА № 7 ОЦЕНКА СВЯЗИ НОМИНАЛЬНЫХ ПРИЗНАКОВ /таблицы сопряженности/ 49

1. Цель работы 49

2. Задание 49

3. Краткая теория 50

4. Ход работы 52

5. Контрольные вопросы 53

ЗАКЛЮЧЕНИЕ 53

ПРИЛОЖЕНИЕ 1 54

Установка надстройки "Пакет анализа" 54

ПРИЛОЖЕНИЕ 2 56

Виды ошибок при задании формул 56

ПРИЛОЖЕНИЕ 3 61

Кратка теория диаграмм 61

ПРИЛОЖЕНИЕ 4 64

Статистические таблицы 64

СПИСОК ЛИТЕРАТУРЫ 70

Учебное издание

Коломийцева Светлана Валерьевна

Чашкин Юрий Романович

Статистическая обработка данных на эвм

Сборник лабораторных работ

Технический редактор Н.В. Мильштейн

—————–––––––––————————————————————————

План 2004 г. Поз. 3.25.

ИД № 05247 от 2.07.2001 г. ПЛД № 79-19 от 19.01.2000 г.

Сдано в набор 31.03.2004 г. Подписано в печать 03.02.2005 г. Формат 6084¹/₁₆. Бумага тип. № 2. Гарнитура Arial. Печать плоская.

Усл. печ. л. 4,4. Зак. 15. Тираж 100 экз. Цена 79 р.

————––––––––—————————————————————————

Издательство ДВГУПС

680021, Г. Хабаровск, ул. Серышева, 47.

Министерство транспорта Российской Федерации

Федеральное агентство железнодорожного транспорта

ГОУ ВПО «Дальневосточный государственный университет путей сообщения»

Кафедра «Прикладная математика»

С.В. Коломийцева Ю.Р. Чашкин

Статистическая обработка данных на эвм

Сборник лабораторных работ

Хабаровск

Издательство ДВГУПС

2005

1 Несмотря на широкое распространение, нормальное распределение не универсально. Если нет уверенности в его применимости, следует проверить возможность использования нормального распределения для описания случайной величины с помощью критериев согласия (см. лаб. работу «Проверка нормальности закона распределения»).

1 Это определение является строгим лишь для распределений экспоненциального типа, например, нормального. В этом случае существует так называемая «граница Крамера-Рао» как минимально возможная дисперсия оценки. Оценка, дисперсия которой достигает этой границы, называется эффективной.

Для распределений с плотностью вероятности, имеющей точки разрыва 1-го или 2-го рода (равномерного, арксинусного, двойного экспоненциального и др.) могут быть построены сверхэффективные оценки (их дисперсия существенно меньше дисперсии среднего арифметического).

1 Одинаковые значения в вариационном ряде должны повторяться столько раз, сколько они встречаются в выборке.

2 Функция ОКРУГЛВВЕРХ округляет число по модулю до ближайшего большего целого. Вторым аргументом является количество цифр, до которого округляется число.

Замечание: Если количество цифр больше 0 (нуля), то число округляется с избытком до заданного количества десятичных разрядов после десятичной запятой. Если количество цифр равно 0 или опущено, то число округляется с избытком до ближайшего целого. Если количество цифр меньше 0, то число округляется с избытком, с учетом десятичных разрядов слева от десятичной запятой.

1 Теоретическая кривая nPj рассчитывается по результатам лаб.раб. №3 «Проверка нормальности…» с помощью критерия согласия . В данной работе может служить огибающей гистограммы. Приводится для наглядности.

1 Отметим, что вопрос о минимальном числе значений в интервале не имеет строгого решения. Автор критерия К.Пирсон считает, что не должно быть пустых интервалов [8]. Мы можем порекомендовать следующий выход из положения: примем . Если при вычислении статистики критерия одно из слагаемых окажется существенно больше остальных, причем будет мало (< 5), объедините этот интервал с соседним.

1 Нужно отметить, что границ интервалов на одно значение больше чем частот, поэтому первому или последнему значению границы интервала будет соответствовать пустая ячейка частоты.

1 функция ФТЕСТ рассчитывает двустороннее -значение F-теста, поэтому для рассматриваемого случая это значение делится на 2.

2 Если то -значение F-теста рассчитывается с помощью функции FРАСП, вычтенной из 1.

1 Сведения о Парном двухвыборочном t-тесте для средних см. в Справочной системе Microsoft Excel.

75