Сравните значения статистических параметров выборки, полученные обоими способами.

5. Контрольные вопросы

1. Что называют прямыми измерениями?

2. Какие измерения являются многократными?

3. Что обычно принимается за результат измерения?

4. Что такое вариационный ряд?

5. Назовите основные характеристики точечных оценок.

6. Каковы преимущества среднего арифметического перед другими оценками?

7. Что является недостатком среднего арифметического?

8. Что такое дисперсия?

9. Что делать, если дисперсия неизвестна?

ЛАБОРАТОРНАЯ РАБОТА № 2 ПОСТРОЕНИЕ ГИСТОГРАММЫ ПО РЕЗУЛЬТАТАМ ПРЯМЫХ МНОГОКРАТНЫХ ИЗМЕРЕНИЙ /на примере результатов математического эксперимента/

1. Цель работы

Цензурирование выборки (исключение промахов).

Освоить основные приемы построения различных гистограмм по результатам многократных измерений, а также элементарной проверки предположения о нормальном законе распределения.

2. Задание

Найти и исключить промахи из выборки.

Построить гистограмму частот или гистограмму статистического распределения. Проверить гипотезу о нормальном законе распределения по ее виду. По имеющейся выборке значений построить доверительный интервал для неизвестного истинного значения.

3. Краткая теория

Поскольку (а следовательно и ) чувствительно к промахам, такой результат (промах) подлежит исключению. Таковыми могут оказаться и . Вопрос об исключении отдельного результата решается с помощью статистических критериев. Вычислив предварительные оценки и , можно проверить и по статистике для резко выделяющихся наблюдений:

, (2.1)

или

. (2.2)

Вычисленные по формулам (2.1) или (2.2) значения статистики следует сравнить с критическим (предельным для данной статистики) значением для уровня значимости . Если вычисленное значение превышает , результат признается промахом и отбрасывается. После исключения промаха вычисления и производят заново без учета отброшенного значения.

Построение гистограммы

Для построения гистограммы вариационный ряд разбивают на интервалы одинаковой, произвольной или специальным образом выбранной длины. В простейшем случае интервалы берут одинаковой длины. Вопрос о необходимом числе интервалов для построения гистограммы не имеет строгого решения. Обычно для определения числа интервалов одинаковой длины пользуются формулой Старджеса:

(2.3)

Ч исло результатов отдельных измерений в каждом интервале называется частотой попадания в k-й интервал, а относительная частота называется в метрологии частностью (мы будем использовать выражение «относительная частота), здесь – общее число измерений. Гистограммой частот будет являться график в виде прямоугольников, причем по оси абсцисс отложены границы интервалов, а по оси ординат – частоты или относительные частоты (рис. 2.1). Ширина прямоугольников равна длине интервала, а высота – соответствующей частоте или относительной частоте. На гистограмме частот сумма всех высот прямоугольников равна , а на гистограмме относительных частот – единице. Для обоих видов гистограмм все интервалы должны иметь одинаковую длину ( называется также шагом гистограммы).

Если по оси ординат отложить величину , то такая гистограмма называется гистограммой статистического распределения, она является выборочной оценкой функции плотности вероятности . Сумма площадей всех прямоугольников на этой гистограмме равна 1. При построении такой гистограммы не обязательно сохранять постоянной длину интервалов.

По любой из этих гистограмм – частот, относительных частот (обе – только с постоянным шагом, иначе возможны значительные искажения формы гистограммы) и статистического распределения – можно составить представление о законе распределения. Удобнее всего это сделать с помощью гистограммы относительных частот. Относительная частота есть оценка вероятности попадания в k-й интервал. Теоретическую вероятность можно вычислить по формуле:

, (2.4)

где – нижняя и верхняя границы k-го интервала; ; – значение интегральной функции стандартного нормального распределения для .

Поскольку при нормальном распределении случайная величина может принимать значения на интервале от до , а в реальном случае интервал конечный ( , ), сумма всех вероятностей по всем r интервалам будет меньше единицы. Проверку правильности вычислений можно осуществить следующими способами:

• вычислить вероятности попадания случайной величины во внешние интервалы ( , ) и ( , ) и прибавить полученные значения к сумме вероятностей по всем r интервалам (в результате должна получиться 1);

• вычислить вероятность попадания случайной величины в интервал ( , ) – эта вероятность должна быть равна сумме вероятностей по всем r интервалам.

Краткие технические сведения о построении различных диаграмм и графиков средствами Excel можно найти в прил. 3 «Теория диаграмм».

Доверительным называется интервал значений, который в последующих опытах накрывает неизвестное истинное значение с вероятностью равной заданной [4, 5].

Для построения доверительного интервала для математического ожидания (истинного значения при центрированных ошибках) воспользуемся соотношением, называемым дробью Стьюдента, которое имеет t-распределение:

, (2.5)

Пользуясь таблицами t-распределения, можно построить доверительный интервал для истинного значения :

(2.6)

где – критическое значение t-распределения при уровне значимости и числе степеней свободы (числе независимых слагаемых в (1.9) и (2.5)) .

Интервал в метрологии называется доверительной случайной погрешностью. Доверительным интервалом по выражению (2.6) пользуются, когда ошибки измерений имеют нормальное распределение. В данной работе предлагается визуально по гистограмме проверить гипотезу о нормальности распределения случайной величины.

Полуширину доверительного интервала можно рассчитать так:

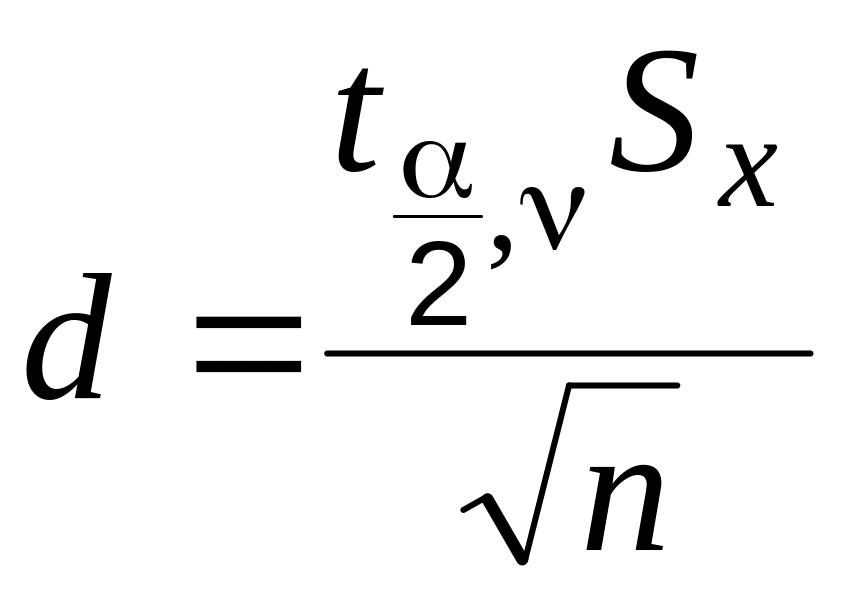, (2.7)

где значения и нужно определить по выборке (лаб. работа «Первичная обработка…»).

Следует при этом иметь в виду, что использование терминов «вероятность» и «доверительная вероятность» применительно к конкретному интервалу , построенному по данной выборке некорректно. Этот интервал может в действительности накрыть неизвестное истинное значение (и тогда следовало бы сказать, что вероятность равна единице), либо не накрыть его (тогда следовало бы сказать, что вероятность равна нулю). Это остается неизвестным исследователю. Однако, если достаточно мало, можно ожидать, что скорее всего накрытие имеет место, то есть доля «накрывающих» интервалов, равная , гораздо больше, чем доля противоположных, равная ). Чтобы отразить нашу уверенность, что скорее всего построенный нами интервал относится к «накрывающим», используется термин «надежность». Надежность численно равна доверительной вероятности:

.

4. Ход работы

1. В книге лабораторных работ по математической статистике Листу2 присвойте оригинальное имя, например, «Гистограмма». Либо выполняйте расчеты на том же листе, что и в предыдущей работе.

2. Выявить и исключить промахи из выборки по методике, описанной в краткой теории, либо см. [9], табл. 4.8 «Критерии исключения резко выделяющихся наблюдений».

3. Постройте гистограмму статистического распределения случайной величины. Для этого выполним несколько шагов:

• О

  

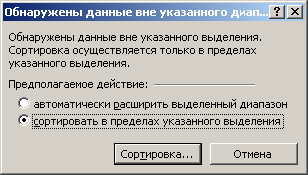
  Рис. 2.2. Вспомогательное диалоговое окно

  тсортируйте выборку в порядке неубывания значений – построение вариационного ряда¹. Для этого придется формулу в каждой ячейке заменить ее значением. Это можно сделать, нажав F9 в строке формул каждой ячейки выборки. Затем необходимо выделить диапазон тех ячеек, которые будут отсортированы и выполнить команду меню Данные-Сортиров­ка... Если появилось окно, представленное на рис. 2.2, укажите вторую опцию (см. рис. 2.2) и нажмите кнопку Сортировка…В диалоговом окне Сортировка диапазона в категории «Сортировать по» укажите нужный столбец и направление сортировки (по возрастанию).

• Вычислите оптимальное число интервалов гистограммы, воспользовавшись, например, формулой Старджеса (2.3). В Excel выражение будет иметь следующий вид: ОКРУГЛВВЕРХ(LOG(25;2)+1;0)². Мы используем эту функцию, чтобы получить целое число интервалов, при этом максимальное значение выборки попадает в последний интервал.

• Вычислите длину каждого интервала h =  . Здесь либо в качестве размаха можно использовать значение показателя Интервал на рис. 1.4.

• Заданную выборку разбейте на вычисленное число интервалов длины h. Для этого к первому значению вариационного ряда прибавьте шаг h – получим первый интервал, к полученному значению снова прибавьте h – получим второй интервал и т.д. до последнего значения вариационного ряда.

• Вычислите частоты попадания значений вариационного ряда в найденные интервалы, для чего воспользуйтесь функцией Excel {=ЧАСТОТА(D2:D26; E9:E14)} как формулой массива (о работе с формулами массива можно почитать в справочной системе Excel или, например, в [15]). Здесь первый аргумент D2:D26 – диапазон значений вариационного ряда, второй аргумент E9:E14 – диапазон значений интервалов для гистограммы.

• Постройте гистограмму статистического распределения с помощью мастера диаграмм Excel. Исходными данными для гистограммы являются найденные интервалы (ось Х) и частоты попадания в них значений вариационного ряда (ось Y).

4. Выполните расчет частот и построение гистограммы с помощью надстройки Пакет анализа:

• Вызовите диалоговое окно Анализ данных (см. рис. 1.1). В категории Инструменты анализа выберите Гистограмма (рис. 2.3).

• В

  

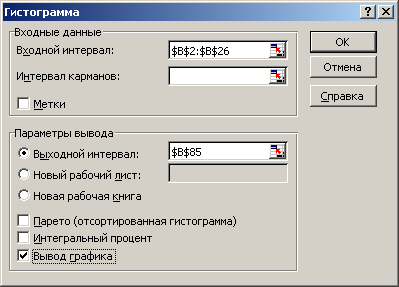
  Рис. 2.3. Диалоговое окно Гистограмма

  поле Входной интервал раздела Входные данные: укажите диапазон значений выборки $B$1:$B$25 (вариационный ряд).

• В поле Интервал карманов (интервалы гистограммы) данные вводить необязательно. В этом случае набор отрезков, равномерно распределенных между минимальным и максимальным значениями данных, будет создан автоматически.

• Введите ссылку на левую верхнюю ячейку выходного диапазона. Размер выходного диапазона будет определен автоматически, и на экран будет выведено сообщение в случае возможного наложения выходного диапазона на исходные данные.

• Установите флажок для автоматического создания встроенной диаграммы на листе, содержащем выходной диапазон. В результате выполнения команды будет рассчитана таблица частот и интервалов гистограммы, а также построен график по данным таблицы. Сравните полученные значения с результатами предыдущих пунктов.

5. По виду гистограммы выполните проверку предположения о нормальном законе распределения значений выборки.

6. Постройте доверительный интервал, накрывающий математическое ожидание случайной величины по значениям выборки, полученной в предыдущей работе. Примерный образец выполнения данной лабораторной работы представлен на рис. 2.4¹.

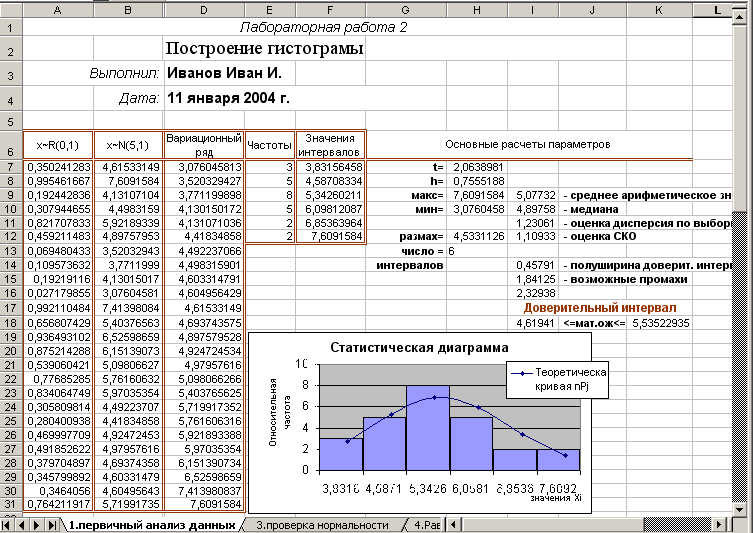
Рис. 2.4. Пример выполнения лабораторной работы

• Для этого, во-первых, найдите коэффициент Стьюдента для числа степеней свободы n-1 (число n вычисляется функцией СЧЁТ(В1:В25) – вычисляется количество заполненных ячеек) и выбранной доверительной вероятности 0,95 (задается произвольно). Воспользуйтесь функцией СТЬЮДРАСПОБР(0,05;СЧЁТ(B1:B25)-1). В качестве первого аргумента функции задается величина 1-0,95; 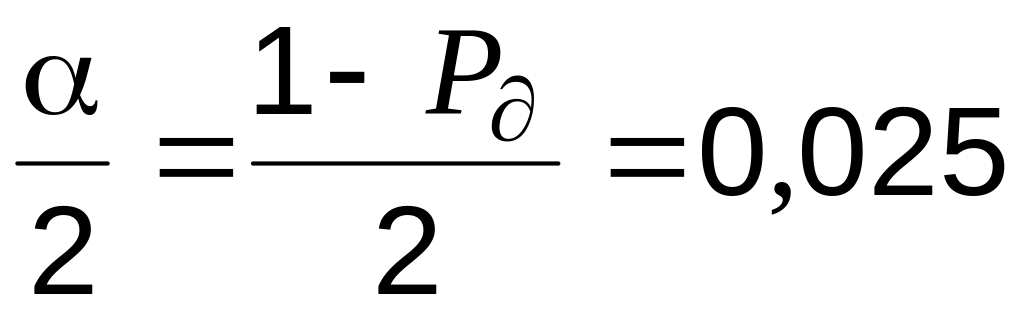, так как 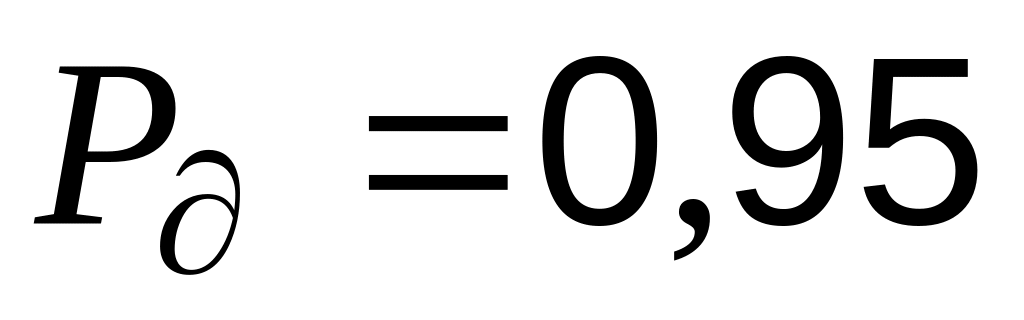(выбранное нами значение доверительной вероятности); второй аргумент – число степеней свободы . Данная функция возвращает t-значение распределения Стьюдента как функцию вероятности и числа степеней свободы, то есть СТЬЮДРАСПОБР=p(t<X), где X – это случайная величина, соответствующая t-распределению.

• Далее вычислите полуширину доверительного интервала по формуле (2.7). В синтаксисе Excel формула примет следующий вид: D1*G4/КОРЕНЬ(СЧЁТ(B1:B25)), где D1 – значение коэффициента Стьюдента, G4 – оценка СКО, функция СЧЕТ(В1:В25) возвращает количество элементов выборки. Построим доверительный интервал для математического ожидания по формуле (2.6).

Замечание. В расчетах мы не воспользовались встроенной функцией Excel ДОВЕРИТ(0,05;F7;СЧЁТ(B1:B25)), которая возвращает доверительный интервал для среднего генеральной совокупности (математического ожидания). Здесь F7 – это стандартное отклонение, которое предполагается известным. Однако в реальном опыте, как правило, нам не известно стандартное отклонение. Мы только можем оценить его значение по выборке.

5. Контрольные вопросы

1. Что такое доверительный интервал? Как его построить средствами Excel?

2. Что такое доверительная вероятность? Надежность?

3. В каком случае результат измерения признается промахом?

4. Что такое гистограмма? Какие виды гистограмм Вы знаете?

5. Как построить гистограмму относительных частот?

6. Каковы особенности гистограммы относительных частот?

7. Как по виду гистограммы проверить предположение о нормальном законе распределения? Убедительно ли свидетельствует гистограмма о нормальности распределения значений выборки?

ЛАБОРАТОРНАЯ РАБОТА № 3 ПРОВЕРКА НОРМАЛЬНОСТИ ЗАКОНА РАСПРЕДЕЛЕНИЯ /тремя различными методами/

1. Цель работы

Освоить основные методы и приемы проверки гипотезы о виде закона распределения результатов измерений.

2. Задание

Выполнить проверку гипотезы о нормальности распределения результатов математического эксперимента графическим методом (методом линеаризации интегральной функции, или методом вероятностной бумаги), с помощью модифицированного критерия Колмогорова и критерия согласия .

3. Краткая теория

При обработке экспериментальных данных и определении погрешности результатов измерений основополагающим является предположение о виде закона распределения ошибок измерений – статистическая гипотеза. Чаще всего предполагается нормальный закон распределения, что должно быть подтверждено объективными методами.

Метод линеаризации интегральной функции распределения.

Для проверки гипотезы о виде закона распределения необходимо расположить результаты измерений в неубывающем порядке – построить вариационный ряд:

.

Эмпирической функцией распределения называют функцию , определяемую соотношением:

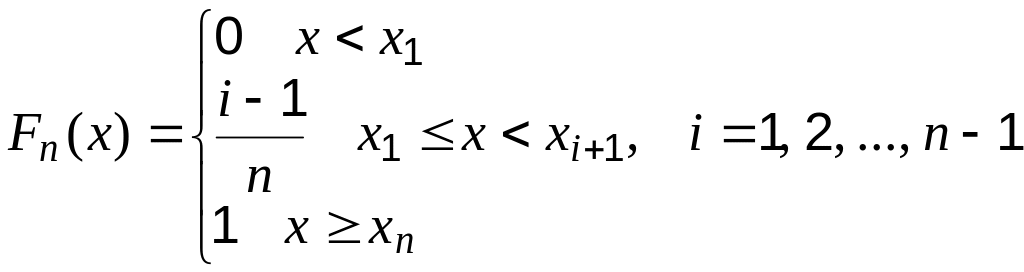. (3.1)

Эмпирическая функция распределения обладает всеми свойствами функции распределения вероятностей и является несмещенной и состоятельной оценкой функции распределения генеральной совокупности, из которой извлечена выборка.

Поставив в соответствие каждому значению вариационного ряды в качестве оценки функции распределения соответствующую долю эмпирической функции распределения, равную (3.1), приравняв ее к функции распределения и, пользуясь таблицами предполагаемого закона распределения (в данном случае – нормального, ), находят теоретические значения аргумента , соответствующие значениям, полученным в опыте для эмпирической функции . Поскольку между и существует линейная зависимость

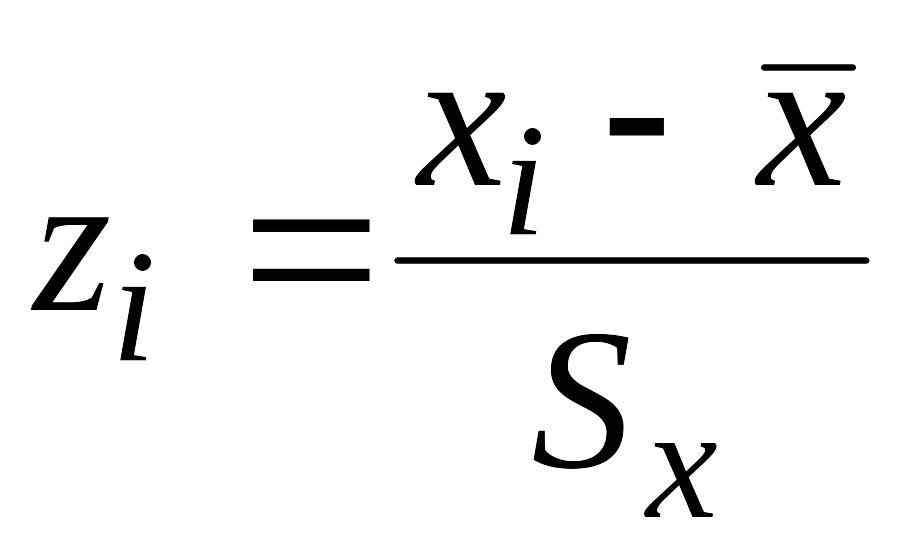(3.2)

(при неизвестных и заменяем их выборочными точечными оценками), характер графика не изменится, если по оси ординат мы отложим значения , а соответствующие им опытные значения отложим по оси абсцисс. Расположение точек на графике вдоль прямой линии подтверждает линейную зависимость между экспериментальными значениями измерений и теоретическими , что свидетельствует о возможности принятия гипотезы о виде закона распределения.

Проведя на глаз прямую через точки, можно по графику приближенно найти оценки и значений и . Значение абсциссы в точке пересечения ее с построенной прямой равно . Значение можно найти из выражения (3.2). Задав любое значение , неравное нулю, по проведенной прямой находят соответствующее ему значение и вычисляют . Если положить = 1, тогда .

Близость графических оценок к вычисленным значения и (см. лабораторную работу № 1) является подтверждением правильности гипотезы о законе распределения.

О графическом методе проверки нормальности закона распределения можно прочитать также в [6, 7, 8].

Проверка гипотез, осуществляемая с помощью статистических критериев, является более объективной. Статистический критерий – это правило, по которому принимается решение по гипотезе. Для построения критерия выбирают статистику – некую функцию от результатов измерений или наблюдений, находят (или заранее знают) ее распределение и (при традиционном подходе к применению статистических критериев) задаются некоторым ее значением, вероятность превышения которого считается пренебрежимо малой. Если наблюденное в опыте значение выбранной статистики оказывается меньше выбранного предельного, то гипотеза принимается, иначе она отвергается. Принятое предельное значение статистики называется критическим.

Уровнем значимости критерия является вероятность попадания статистики критерия в критическую область (когда гипотеза верна, но критерий ее отвергает, поэтому вероятность называется также вероятностью ошибки 1-го рода), здесь – вероятность попадания в допустимую область (в интервал вероятности). Значение считается таким, когда шансы принять неверную гипотезу или отвергнуть правильную гипотезу, приблизительно равны.

Применение критерия Колмогорова

График функции представляет собой ступенчатую фигуру со скачками, равными или кратными величине в точках, определяемых членами вариационного ряда. Как оценка функция случайна. Допустимые (с задаваемой вероятностью) отклонения ее от даются критерием Колмогорова, использующего статистику в виде

, (3.3)

т.е. для любых конечных значений х статистика представляет собой самое большое по модулю отклонение от .

Для практических вычислений [9] удобнее использовать следующие формулы:

, , .

Критерий Колмогорова имеет вид [9]:

, (3.4)

где – верхний -предел статистики при объеме выборки .

Критерий Колмогорова применим при любом законе распределения (то есть, он свободен от распределения), если – непрерывная функция, причем не зависит от выборки, т. е. не зависит от ; здесь x_i – элементы вариационного ряда (упорядоченной выборки).

Если же связана с выборкой (содержит выборочные оценки математического ожидания и дисперсии , как при проверке гипотезы о нормальном распределении – обозначим эту функцию распределения ), то критерием Колмогорова пользоваться нельзя [10], т.к. границы в правой части (3.4) оказываются заметно меньше, причем это уменьшение оказывается разным при разных законах распределения. Экспериментальные исследования границ ( -пределов статистики ) выполнены Стефенсом (см. [10, 11]). Для нормального распределения границы Стефенса хорошо аппроксимируются для и выражением [5]

, (3.5)

где значения берутся из таблиц статистики Колмогорова [9] или вычисляются по формуле

, (3.6)

где (для ) или (для ).

Если в критерии Колмогорова (3.4) использовать новые границы (3.5), то критерий становится модифицированным критерием Колмогорова. Модифицированный критерий Колмогорова оказывается зависим от распределения, он становится параметрическим, разным для разных законов распределения. Однако важнейшее [11] его свойство сохраняется – он работает с негруппированными данными и полностью использует всю информацию, содержащуюся в выборке.

Применение критерия согласия

При объеме выборки для проверки гипотезы о виде распределения применяют критерий согласия (критерий Пирсона), широко представленный в литературе [2,10,11] и широко распространенный на практике. Он применяется для группированных данных (как при построении гистограммы), когда в каждом интервале находится не менее 5 измерений. Если число измерений в интервале оказывается меньше 5, этот интервал объединяют с соседним¹.

Критерий согласия имеет вид

, (3.7)

где – число данных в k-м интервале (k = 1, 2, …, r); – теоретическая вероятность попадания случайной величины х в k-й интервал, равная при нормальном законе

, (3.8)

где – нижняя, а – верхняя границы интервала; – теоретическая интегральная функция нормированного нормального распределения; – объем выборки; r – число интервалов; – число степеней свободы; j – число параметров закона распределения, определяемых по выборке.

В случае нормального закона распределения j = 2, так как по выборке оцениваются два параметра распределения – математическое ожидание и дисперсия.

Вычисленное по выражению (3.7) значение сравнивается с табличным для распределения при выбранном уровне значимости . Если , то гипотеза о виде распределения принимается, в противном случае она отвергается и строится новая гипотеза – предлагается другой закон.

На практике критерием (3.7) пользуются при объеме выборки  (40–50), при этом необходимо помнить, что в этом случае критерий (3.7) обладает повышенной вероятностью ошибки 1-го рода (признать неверной проверяемую гипотезу, когда она верна). Если выборка имеет малый объем и выводы о виде закона распределения по критериям Колмогорова и Пирсона окажутся противоречащими друг другу, предпочтение должно быть отдано критерию Колмогорова.

4. Ход работы

Метод линеаризации интегральной функции распределения

1. В книге лабораторных работ по математической статистике Листу3 присвойте оригинальное имя, например, «Проверка нормальности».

2. Для проверки закона распределения методом линеаризации постройте данные в виде табл. 3.1.

Таблица 3.1

3. Получите x_i~N(5,1) – выборку случайных чисел, распределенных по нормальному закону, с математическим ожиданием равным 5, и стандартным отклонением равным 1 (для этого выполните шаги п.2, лабораторной работы № 1). Можно использовать данные, полученные в указанной лабораторной работе, выполнив ссылку на соответствующий лист.

4. Постройте вариационный ряд, упорядочив полученные значения по неубыванию. Результат поместите в столбец 2 табл. 3.1.

5. Вычислите значения эмпирической функции распределения вероятностей F_n(х_i) = 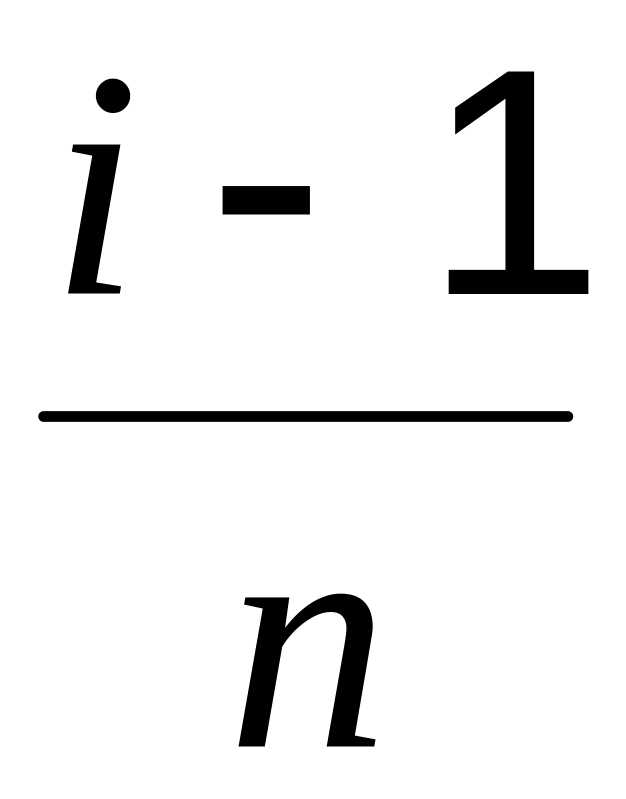, где i – номер точки в упорядоченной выборке (столбец 3 таблицы 3.1).

• Для вычисления значений функции в отдельной ячейке подсчитайте количество элементов выборки, используя функцию СЧЁТ(D4:D28). Диапазон D4:D28 содержит значения вариационного ряда х_i.

• Постройте вспомогательный столбец номеров i точек вариационного ряда. Для этого в строке, соответствующей первому значению вариационного ряда, запишем 1. Удерживая клавишу CTRL, выполним автоматическое заполнение ячеек столбца номеров. При заполнении Excel указывает текущее значение номера (столбец 1 табл. 3.1).

6. Найдите теоретические значения аргумента, соответствующие значениям, полученным в опыте для эмпирической функции F_n(x_i) , где 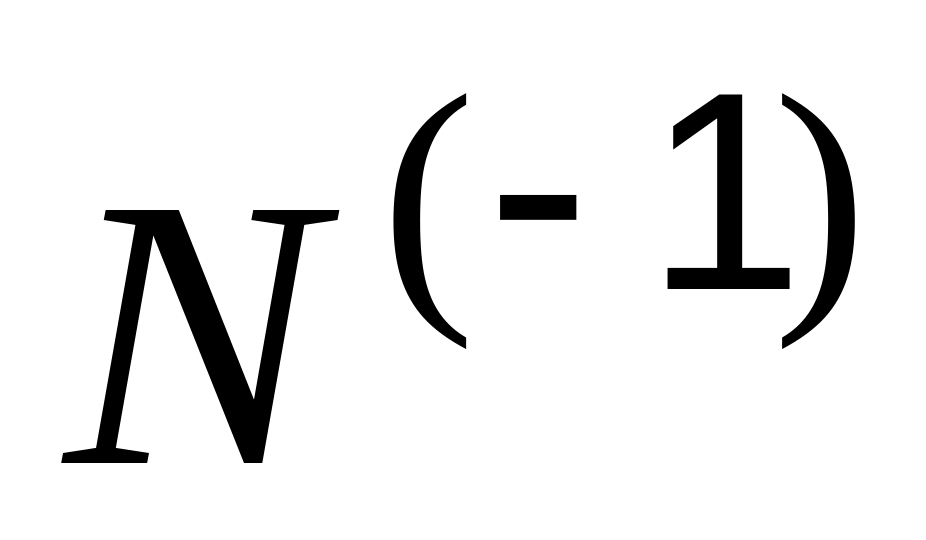– функция обратного нормального распределения. Для этого используйте функцию Excel НОРМСТОБР(), аргументом которой является значение функции F_n(Z_i) (столбец 4 табл. 3.1).

7. 

   Рис. 3.1. График точек с прямой

   Постройте график точек , используя мас­тер диаграмм (рис. 3.1).

8. Для точек функции добавьте линию тренда (одноименная функция контекстного меню рядов данных) (рис. 3.1). Изменяя параметры линейной аппроксимации, добейтесь наилучшего приближения прямой к точкам, не учитывая при этом по 1–2 крайние точки с каждой стороны. Это можно сделать, установив значение точки пересечения кривой с осью Y в диалоговом окне «Формат линии тренда», вкладка «Параметры».

9. Вычислите по графику приближенные значения среднего арифметического 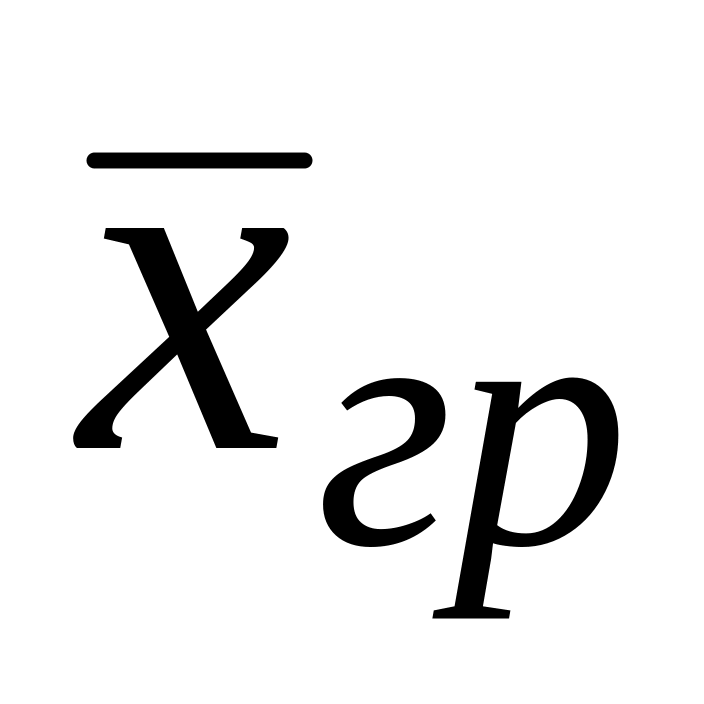(точка пересечения прямой тренда с осью абсцисс) и оценки СКО 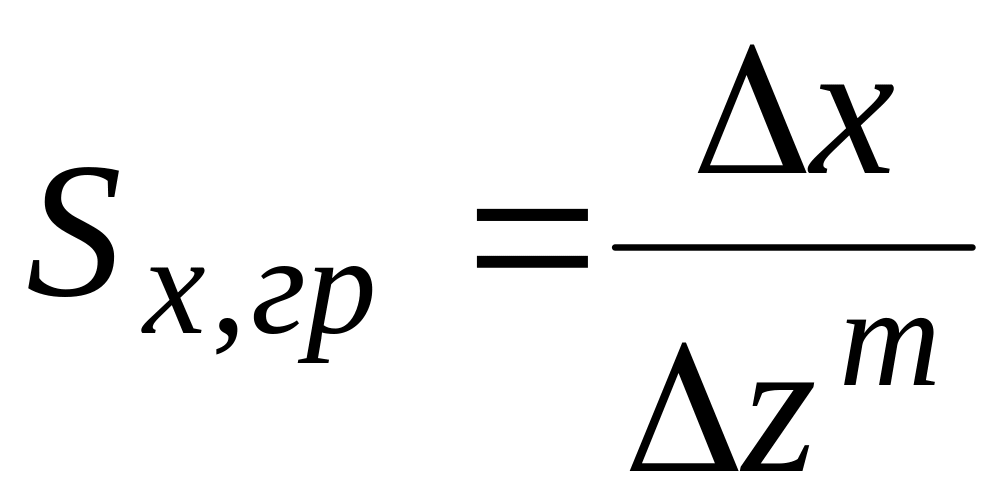. Близость графических оценок к вычисленным значениям 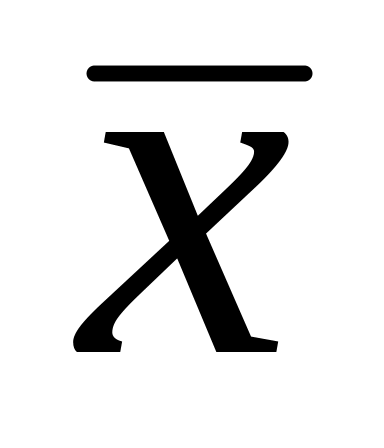и (см. работу № 1) является подтверждением правильности гипотезы о законе распределения.

Применение модифицированного критерия Колмогорова

1. Используя упорядоченные массивы х_i~N(5,1) и F_n(х_i) = , вычислите значения функции распределения вероятностей F(х_i, , ):

• Вычислите значения оценки СКО и среднего арифметического для исходной выборки в отдельных ячейках, используя стандартные статистические функции (см. работу № 1).

• z_i для распределения, характеризуемого средним и стандартным отклонением по формуле (3.2).

• Значения функции распределения вероятностей F вычислите с помощью функции НОРМРАСП(x;среднее;СКО;1), которая возвращает нормальную функцию распределения для указанного среднего и СКО. Последний аргумент определяет вид функции: 1 означает, что функция НОРМРАСП возвращает интегральную функцию распределения; 0 –возвращается функция плотности распределения. Уравнение для плотности нормального распределения имеет вид:

.

• Вычислите абсолютные значения отклонений эмпирической функции распределения от теоретической в отдельном столбце (диапазон N4:N28) и найдите максимальное из них (3.3), используя функцию МАКС(N4:N28).

2. Вычислите 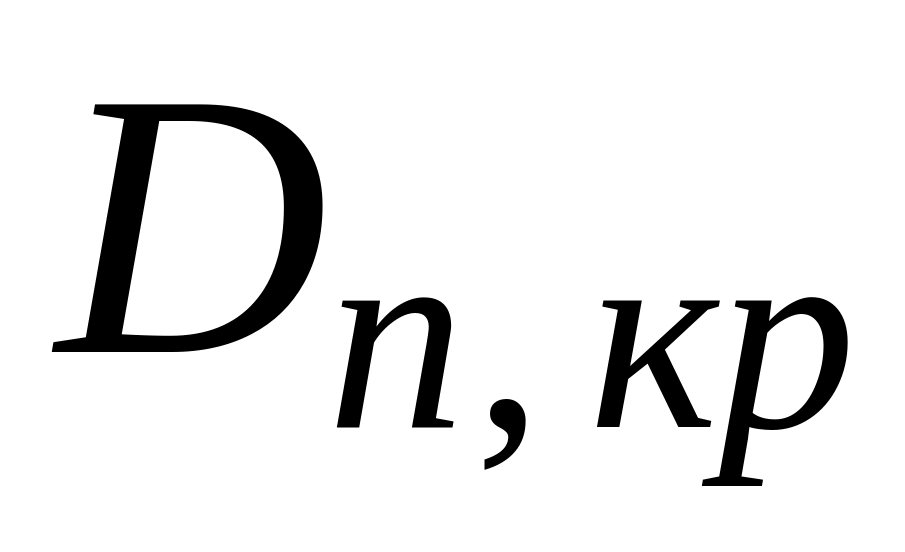для выбранного уровня значимости приближенным выражением

.

3. Наконец найдите значение модифицированного критерия Колмогорова (3.5). Если выполняется условие 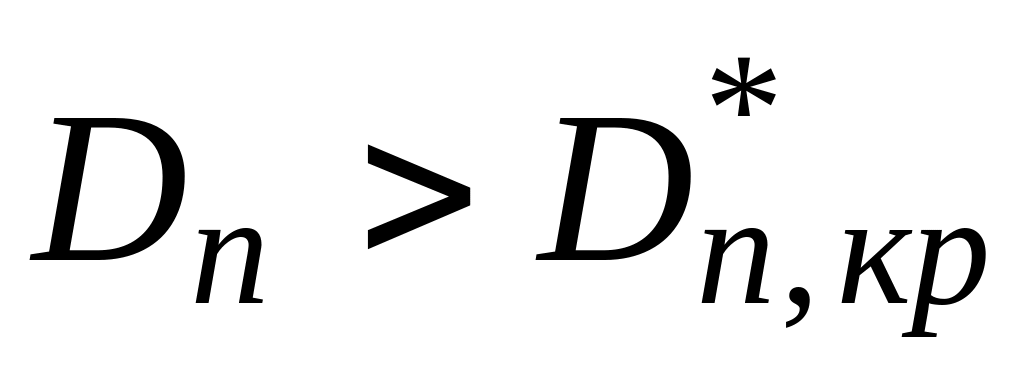гипотеза о нормальности отвергается, в противном случае гипотеза принимается.

Использование критерия согласия

1. Для проверки закона распределения по критерию согласия Пирсона постройте данные в виде табл. 3.2.

Таблица 3.2

2. Заполните столбец 1, автоматическим заполнением ячеек.

3. В ячейки столбца 2 внесите ссылки на ячейки столбца значений границ интервалов, расположенных на листе построения гистограммы относительных частот. Число значений в интервале равно соответствующей частоте попадания значений вариационного ряда в интервал¹.

4. Вычислите значения теоретической вероятности (столбец 5):

• Вычислите для каждой границы интервала ее нормированное значение по формуле (3.2). Для этого воспользуйтесь функцией НОРМАЛИЗАЦИЯ(х;среднее;СКО) (столбец 4 табл. 3.2).

• Используя полученные значения в качестве аргумента, вычислите теоретическую интегральную функцию нормированного нормального распределения 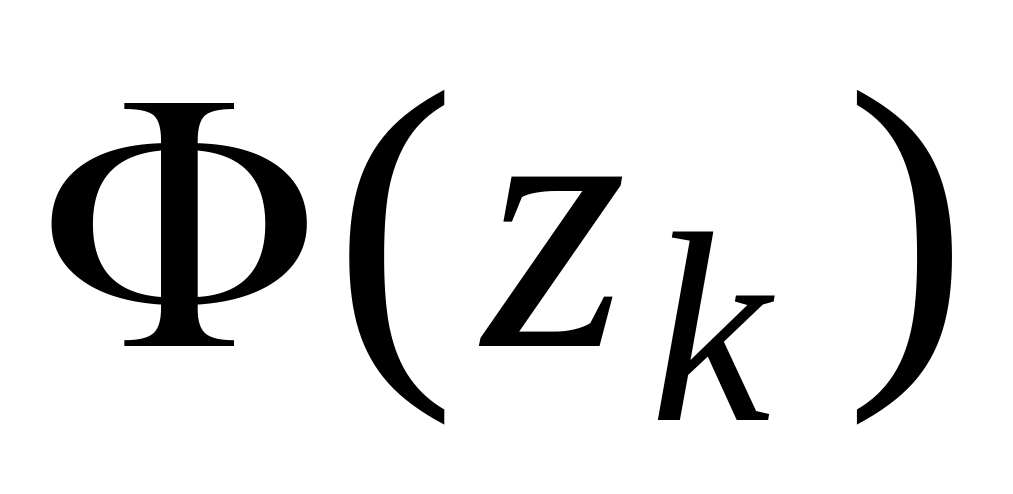. Функция Excel НОРМРАСП. Значения аргументов: среднего = 0, оценка СКО = 1, так как значения границ уже нормированы.

• Далее по формуле (3.8) вычислите значения теоретической вероятности .

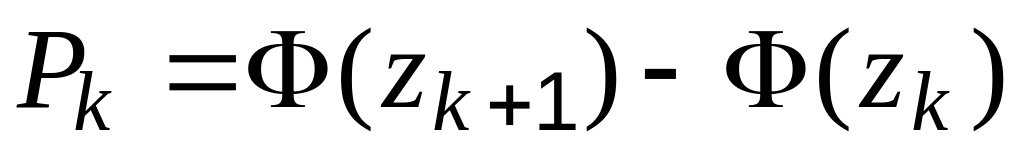5. Заполните столбец 6, предварительно вычислив объем выборки (функция СЧЕТ). Для контроля правильности вычислений выполните суммирование значений ячеек столбца 6 – результат должен быть немного меньше 1 (см. раздел 3, п. «Построение гистограммы» лабораторной работы № 2).

• Постройте график зависимости от значений середин интервалов. Результатом является теоретическая кривая нормального распределения. Сравните с графиком гистограммы, полученной в работе № 2.

6. Отдельно вычислите значение статистики критерия согласия Пирсона по формуле (3.7), предварительно заполнив ячейки столбца 7. Вычисленное значение сравнивается с табличным (критическим) при выбранном одностороннем уровне значимости . Если 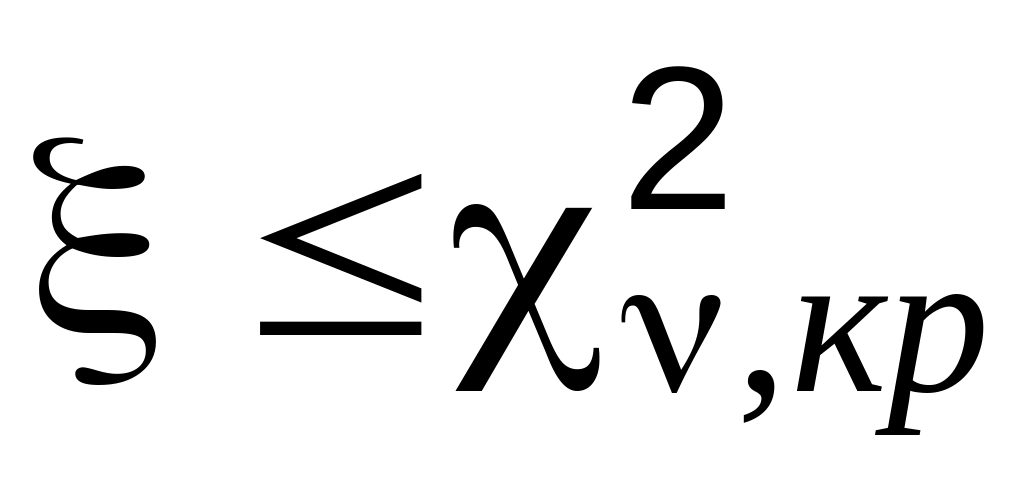, то гипотеза о виде распределения принимается. Критическое значение статистики критерия можно вычислить с помощью функции ХИ2РАСП(x;степени_свободы), которая возвращает одностороннюю вероятность распределения . х – это значение, для которого требуется вычислить распределение. В нашем случае это значение статистики критерия согласия Пирсона, вычисленное по формуле (3.7). Степени_свободы – это число степеней свободы.

7. Для вычисления уровня значимости наблюденного значения статистики , т.е. такого значения , при котором значение критерия становится критическим, можно воспользоваться методом интерполяции табличных значений -распределения или приближенным выражением [6]:

,

где .

Решите обе задачи использования критерия Пирсона: п.6 и п.7. Сравните результаты вычислений.

5. Контрольные вопросы

1. В чем заключается метод линеаризации интегральной функции распределения проверки гипотезы о виде закона распределения?

2. Что такое статистические критерии?

3. Что показывает уровень значимости статистического критерия?

4. Как используется критерий Колмогорова?

5. Как используется критерий согласия Пирсона?

6. Что делать если при объеме выборки 20 критерий Колмогорова и Пирсона дают противоречивые результаты?

ЛАБОРАТОРНАЯ РАБОТА № 4 ОБЪЕДИНЕНИЕ РАВНОТОЧНЫХ СЕРИЙ ИЗМЕРЕНИЙ /двухвыборочный t-тест для средних/

1. Цель работы

Изучить основные особенности и методы объединения результатов разных серий измерений в общий массив значений.

2. Задание

Выполнить объединение двух выборок разного объема из одной генеральной совокупности при отсутствии систематических ошибок и нормальном законе распределения случайных ошибок измерений, используя двухвыборочный t-критерий.

3. Краткая теория

Предположим, что измерительную информацию о некоторой физической величине постоянного размера получают сериями – в разное время, в разных условиях, разными методами, разные операторы. Если объединить все результаты измерений в общий массив, то можно было бы получить более точный и надежный результат за счет увеличения объема выборки. Однако такое объединение возможно только при условии, что вид закона распределения (например, нормальный) обеих выборок один и тот же и математические ожидания у них равны (дисперсии могут быть различны).

В математической статистике однородными называются серии (выборки), взятые из одной генеральной совокупности, то есть имеющие одинаковый вид закона распределения, одинаковые математические ожидания и одинаковые дисперсии. В метрологии однородные серии могут иметь различные дисперсии [2].

Если дисперсии в сериях одинаковы (не выборочные их оценки, а сами дисперсии), то в простейшем случае для двух серий измерений критерий однородности (t-критерий) имеет вид [4, 5, 7, 8, 11]:

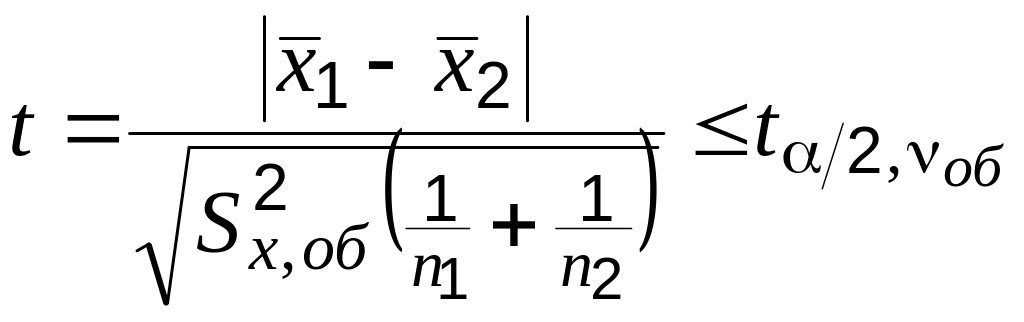, (4.1)

где и – средние арифметические в сериях; и – объемы серий; – табличное значение t-статистики; – объединенная оценка дисперсии :

, (4.2)

где и – выборочные оценки дисперсии в сериях; – число степеней свободы оценки и табличного значения t-статистики .

Прежде чем воспользоваться критерием (4.1), необходимо убедиться, что и есть оценки одной и той же дисперсии . Только в этом случае может быть использована объединенная оценка дисперсии в виде выражения (4.2). Проверка гипотезы о равенстве дисперсий в сериях при нормальном распределении осуществляется с помощью F-критерия (критерия дисперсионного отношения) [4, 5, 7, 8, 11]:

, (4.3)

где – максимальная из двух оценок и ; – число степеней свободы числителя ( ); – минимальная из двух оценок, – число степеней свободы знаменателя. Значение берется из таблиц F-распределения при одностороннем уровне значимости и числах степеней свободы числителя и знаменателя .

Если условие (4.3) выполняется, гипотеза о равенстве дисперсий принимается на уровне значимости . В противном случае она отвергается.

Если условия (4.3) и (4.1) выполняются, делается вывод о равноточности и однородности серий. В этом случае все экспериментальные данные объединяются и обрабатываются как единый массив, для которого вычисляются оценки основных статистических параметров:

. (4.4)

Поскольку для серий оценки и обычно бывают уже вычислены, то удобнее пользоваться другими формулами. Для двух серий они имеют вид

, (4.5)

где – общее число данных объединенного массива.

Критериями (4.1) и (4.3) можно пользоваться и тогда, когда число серий больше двух, но в сериях приблизительно одинаковы. Если серии с максимально различающимися и не будут отвергнуты критериями, тогда и остальные серии принимаются к объединению.

При построении t-интервала для истинного значения в случае объединения равноточных серий берут число степеней свободы .

4. Ход работы

1. Получите n1_i и n2_i из N(5;1), – две серии случайных чисел, распределенных по нормальному закону, с математическим ожиданием равным 5, и дисперсией 1 (для этого выполните шаги п.2 или п.3, лабораторной работы № 1). Размерность серий может быть произвольной, необязательно одинаковой.

2. Выполните расчет двухвыборочного F-теста для дисперсий, используя одноименный инструмент надстройки Анализ данных (см. рис. 4.1).

Примерный вид результатов работы надстройки «Двухвыборочный F-тест для дисперсий» представлен на рис. 4.2.

Рис. 4.1. Двухвыборочный F-тест для дисперсий

3. Проверьте гипотезу = 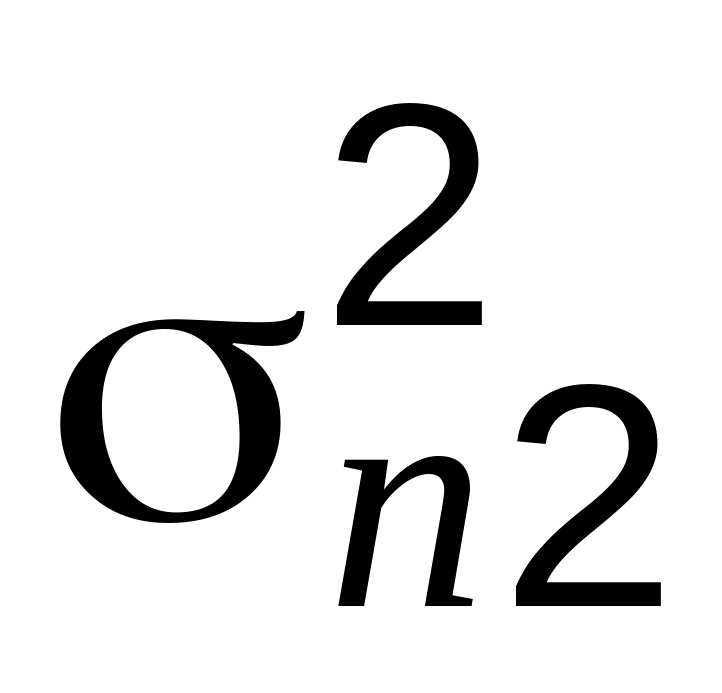о равенстве дисперсий в сериях n1 и n2 по таблице значений параметров надстройки «Двухвыборочный F-тест для дисперсий» (рис. 4.2).

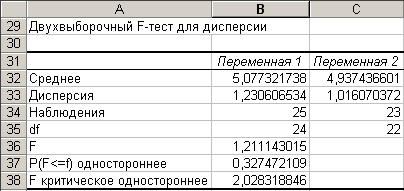
Рис. 4.2. Примерный результат расчета F-теста

• Число степеней свободы (показатель df) рассчитывается в ячейках В35 и С35 по формулам =В34-1 и =С34-1 соответственно.

• Значение критерия F вычисляется в ячейке В36 по формуле =В33/С33, где в ячейках В33 и С33 рассчитываются оценки дисперсии с помощью функции ДИСП (сведения о функции ДИСП см. в лаб. работе № 1). Это соответствует формуле (4.3). В случае, когда при расчете двухвыборочного F-теста для дисперсий в качестве интервала переменной 1 (рис. 4.1) выбирается выборка с меньшей дисперсией, то для соответствия с формулой (4.3) необходимо найти значение F, обратное вычисленному в ячейке В36.

• Значение Р(F=f) показывает уровень значимости, при котором значение F становится критическим.

• Значение показателя F критическое одностороннее определяется в ячейке В38 по формуле =FРАСПОБР(1-0,05;В35;С35), которая рассчитывает обратное F-распределение. Функция используется в ситуациях, когда известен уровень надежности (или уровень значимости) и необходимо рассчитать значение F-критерия. Первый аргумент – вероятность, соответствующая двустороннему F-распределению (уровень значимости . Второй аргумент – число степеней свободы для первой выборки n1. Третий аргумент – число степеней свободы для второй выборки n2. Замечания: если вероятность < 0 или вероятность > 1, то функция FРАСПОБР возвращает значение ошибки #ЧИСЛО!; если степени_свободы1 или степени_свободы2 не целое число, то оно усекается; функция FРАСПОБР использует метод итераций для вычисления значения и производит вычисления, пока не получит результат с точностью  310^-7. Если результат не сходится после 100 итераций, то функция возвращает значение ошибки #Н/Д.

• Можно получить двустороннюю оценку F_кр., используя функцию FРАСПОБР при уровне значимости 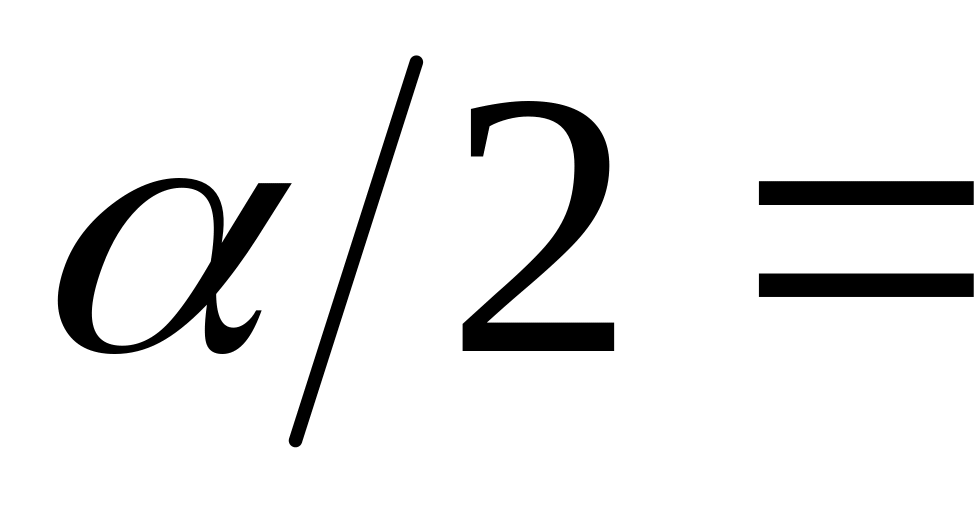0,025. Тогда формула =FРАСПОБР (1-0,025; В35; С35) рассчитает значение левосторонней критической точки = 0,43555736, а формула =FРАСПОБР(0,025; В35; С35) – значение правосторонней критической точки = 2,331503879. Таким образом, при двусторонней оценке получим критическую область как объединение двух интервалов . Однако и в случае двусторонних оценок значение критерия F не принадлежит ни одному критическому интервалу, следовательно, гипотеза принимается.

• Сравните расчетное значение F с параметром F критическое одностороннее по формуле (4.3), если F F_кр., гипотеза 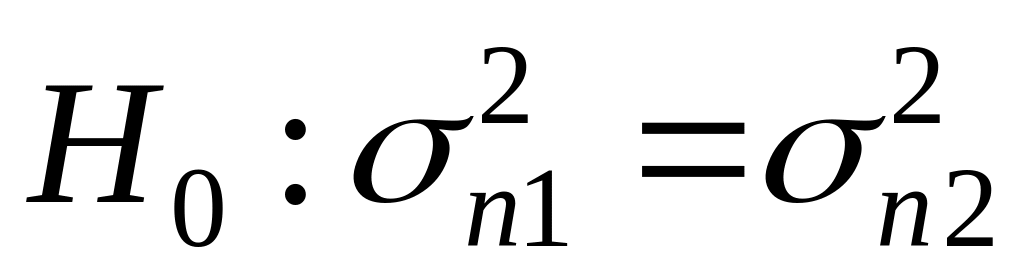также принимается.

• Для расчета значения параметра Р(F<=f) одностороннее в ячейке В37 (рис.4.2) можно использовать следующие функции, родственные режиму «Двухвыборочный F-тест для дисперсий».

Функция FРАСП

Синтаксис:

FРАСП(х; степени_свободы1; степени_свободы2)

Рассчитывает значение вероятности F-распределения (распределения Фишера). Х – значение, для которого вычисляется F-распределение. Степени_свободы1 – число степеней свободы для первой выборки n1. Степени_свободы2 – число степеней свободы для второй выборки n2.

Замечания:

• если какой-либо аргумент не является числом, то функция FРАСП возвращает значение ошибки #ЗНАЧ!;

• если аргумент степени_свободы1 или степени_свободы2 не целое число, то оно усекается;

• если аргумент степени_свободы1 или степени_свободы2 меньше 1 или больше 10¹⁰, то функция FРАСП возвращает значение ошибки #ЧИСЛО!.

Распределение Фишера (оно иногда называется распределением Снедеко­ра, Снедекора–Фишера, Фишера–Снедекора или распределением дисперсионного отношения) – это распределение случайной величины в виде отношения двух независимых случайных величин , каждая из которых имеет распре­деление , где – число степеней свободы. Связь между -распре­де­лением и распределением , таким образом, дается формулой:

.

распределение Фишера со степенями свободы и . На практике чаще применяется функция FРАСПОБР.

Функция ФТЕСТ

Синтаксис:

ФТЕСТ(массив1; массив2)

Рассчитывает для двух выборочных массивов данных двустороннее -значение F-теста. Массив1 – первая выборка данных. Массив2 – вторая выборка данных.

Замечания:

• аргументы должны быть числами или именами, массивами или ссылками, содержащими числа;

• если аргумент, который является массивом или ссылкой, содержит текстовые значения или пустые ячейки, то такие значения игнорируются; однако ячейки с нулевыми значениями учитываются;

• если количество точек данных в аргументе массив1 или массив2 меньше 2 или если дисперсия аргумента массив1 или массив2 равна 0, то функция ФТЕСТ возвращает значение ошибки #ДЕЛ/0!.

Для наших данных (рис. 5.2) Р(F<=f) одностороннее в ячейке В77 рассчитывается по формуле =ФТЕСТ(A43:B62;C43:C67)/2¹, которая оказывается адекватна формуле =FРАСП(F49;F48;G48)².

4. Если дисперсии в сериях одинаковы, проверим однородность серий по формуле (4.1). Для этого воспользуемся режимом «Двухвыборочный t-тест с одинаковыми дисперсиями» надстройки Анализ данных… Microsoft Excel (рис. 4.3).

Рис. 4.3. Двухвыборочный t-тест c одинаковыми дисперсиями

Таблица значений, рассчитанных с использованием надстройки «Двухвыборочный t-тест с одинаковыми дисперсиями» представлена на рис. 4.4.

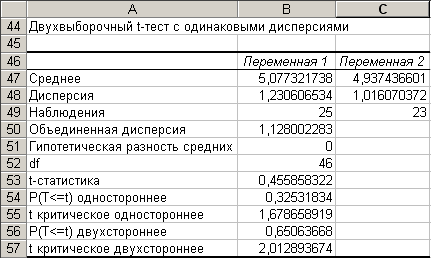
Рис. 4.4. Таблица расчетных значений двухвыборочного t-теста

4. Проверьте однородность (гипотезу о равенстве математических ожиданий) серий измерений по таблице значений параметров надстройки «Двухвыборочный t-тест с одинаковыми дисперсиями» (рис. 4.4).

   • Значения Среднего (ячейки В47 и С47), Дисперсии (ячейки В48 и С48) рассчитываются с помощью соответствующих функций, описанных в лаб. работе № 1.

   • Объединенная оценка дисперсии (ячейка В50) рассчитывается по формуле (4.2). В синтаксисе Excel формула примет следующий вид: =((B49-1)*B48+(C49-1)*C48)/(B49+C49-2).

   • Число степеней свободы (показатель df) рассчитывается в ячейке В52 по формуле =B49+C49-2 как и полагается для .

   • Основной показатель данной надстройки t-статистика вычисляется согласно формуле (4.1). В синтаксисе Excel формула примет следующий вид:

=ABS(B47-C47)/КОРЕНЬ(B50*(1/СЧЁТ(A3:A27)+1/СЧЁТ(B3:B25)))

Здесь значения функций, применяемых в формуле интуитивно понятны. В случае сомнений см. Справочную систему Excel. Диапазоны A3:A27 и B3:B25 содержат значения первой и второй выборок соответственно.

• Модуль значения t критического двустороннего вычисляется в ячейке В57 по формуле =СТЬЮДРАСПОБР(0,05;B52). Сведения по функции СТЬЮДРАСПОБР можно найти в лаб. работе № 2.

• Для расчета значения одностороннего (ячейка В54) и двустороннего (ячейка В56) -значения t-теста можно использовать функцию ТТЕСТ, родственную режиму «Двухвыборочный t-тест с одинаковыми дисперсиями» (рис. 4.4).

Функция ТТЕСТ

Синтаксис:

ТТЕСТ(массив1; массив2; хвосты; тип)

Возвращает вероятность, соответствующую критерию Стьюдента. Функция ТТЕСТ используется, чтобы определить, насколько вероятно, что две выборки взяты из генеральных совокупностей, которые имеют одно и то же среднее. Массив1 – первое множество данных. Массив2 – второе множество данных. Хвосты – число хвостов распределения. Если хвосты = 1, то функция ТТЕСТ использует одностороннее распределение. Если хвосты = 2, то функция ТТЕСТ использует двустороннее распределение. Тип – вид исполняемого t-теста.

Замечания:

• Если массив1 и массив2 имеют различное число точек данных, а тип = 1 (парный), то функция ТТЕСТ возвращает значение ошибки #Н/Д.

• Аргументы хвосты и тип усекаются до целых.

• Если хвосты или тип не является числом, то функция ТТЕСТ возвращает значение ошибки #ЗНАЧ!.

• Если хвосты имеет значение, отличное от 1 и 2, то функция ТТЕСТ возвращает значение ошибки #ЧИСЛО!.

Для случая равных дисперсий P(T<=t) одностороннее (ячейка В54 рис. 4.4) вычисляется по формуле

=ТТЕСТ(A3:A27;B3:B25;1;2),

которая адекватна формуле

=СТЬЮДРАСП(B53;B52;1),

а P(T<=t) двустороннее (ячейка В56 рис. 4.4) вычисляется по формуле

=ТТЕСТ(A3:A27;B3:B25;2;2),

которая адекватна формуле

=СТЬЮДРАСП(B53;B52;2).

Функция СТЬЮДРАСП возвращает вероятность для t-распределения Стьюдента, а численное значение (аргумент В53) – это вычисленное значение, для которого должны быть вычислены вероятности. Данную функцию можно использовать вместо таблицы критических значений t-распределения.

• Сравните значение t-статистики = 0,455858321612874 с t критическим односторонним или двусторонним. Для выполнения гипотезы критическая область образуется объединением интервалов 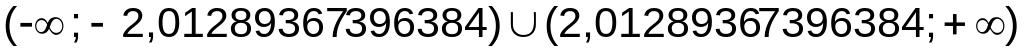. Так как условие (4.1) выполняется, т.е. значение t-статистики не попадает ни в один критический интервал, то гипотезу о равенстве математических ожиданий принимаем.

После объединения однородных серий результатов измерений выполните расчет основных статистических параметров, используя, например, режим «Описательная статистика» (см. лаб. работу № 1).