Министерство транспорта Российской Федерации

Федеральное агентство железнодорожного транспорта

ГОУ ВПО «Дальневосточный государственный университет путей сообщения»

Кафедра «Прикладная математика»

С.В. Коломийцева Ю.Р. Чашкин

Статистическая обработка данных на эвм

Сборник лабораторных работ

Рекомендовано методическим советом ДВГУПС в качестве учебного пособия

Хабаровск

Издательство ДВГУПС

2005

УДК 519.2:004.6 (075.8) ББК В 172я73+З973.2-018я73

К 612

Рецензенты:

доктор технических наук, зав. кафедрой «Прикладная математика» ДВГУПС, профессор А.И. Кондратьев

Кандидат технических наук, директор ВНИИФТИ (Дальстандарт)

Ю.И. Лыков

Кафедра «Высшая математика» Хабаровского государственного технического университета (заведующий кафедрой, профессор А.Г. Подгаев)

Коломийцева, С.В.

К 612 Статистическая обработка данных на ЭВМ: Сборник лабораторных работ / С.В. Коломийцева, Ю.Р. Чашкин. – Хабаровск: Изд-во ДВГУПС, 2005. – 74 с.

Сборник лабораторных работ соответствует ГОС ВПО направления 010500 «Прикладная математика и информатика».

Сборник содержит основные теоретические сведения математической статистики, а также задания для самостоятельных или лабораторных работ студентов по изучению методов и приемов первичной статистической обработки экспериментальных данных, содержащих случайные ошибки с помощью табличного процессора Microsoft Excel 2000 пакета Microsoft Office 2000 для операционной системы Windows.

Сборник предназначен для студентов 3 курса естественнонаучных и технических специальностей, изучающих математическую статистику, которым необходимо умение грамотно обработать результаты измерений. Он может быть использован и для других специальностей, использующих статистическую обработку данных.

Данный курс рассчитан на 7 занятий и предполагает наличие начального опыта работы с Microsoft Excel.

© ГОУ ВПО «Дальневосточный государственный университет путей сообщения» (ДВГУПС), 2005

Введение

В современном обществе к статистическим методам проявляется повышенный интерес как к одному из важнейших аналитических инструментариев в сфере поддержки процессов принятия решений. Большим шагом вперед к развитию статистической науки послужило применение экономико-математических методов и использование компьютерной техники в анализе различных явлений.

Цель данной работы – закрепление теоретических знаний студентов и приобретение ими практических навыков по статистической обработке результатов измерений начиная с простейшего построения вариационного ряда и гистограммы, идентификации закона распределения с помощью различных статистических критериев, заканчивая вопросами построения эмпирической зависимости при известном и неизвестном виде истинной зависимости и оценкой погрешности результатов. В качестве инструмента, с помощью которого студенты могут выполнять задания каждой из лабораторных работ, используется табличный процессор Microsoft Excel 2000, который входит в состав пакета программ Microsoft Office 2000 Professional для Microsoft Windows 2000.

Пакет предоставляет набор функций, характерных для систем обработки данных: анализ, графическая интерпретация, создание выборок случайных чисел, имеющих различные типы распределения и работа с ними; а также автоматизацию своих функций в записываемых макросах. Кроме того, пакет содержит ряд надстроек, позволяющих оптимизировать работу по анализу данных и принятию решений, о которых почти не упоминается в литературе [1].

Excel не является идеальным средством для статистической обработки экспериментальных данных, но он выбран, так как является наиболее распространенным в деловой сфере, универсальным программным продуктом, и поэтому нет необходимости подробно описывать интерфейс Excel и давать навыки работы с ним.

Настоящий сборник содержит краткие сведения из метрологии и математической статистики, касающиеся выполнения заданий в каждой лабораторной работе, однако это отнюдь не заменяет использование учебной и справочной литературы, список которой приведен в конце работы. Кроме того, в конце каждого раздела предлагается ответить на вопросы самоконтроля для лучшего усвоения материала.

Поскольку навыков работы с пакетом программ может быть недостаточно, в прил. 4 приведены краткие статистические таблицы, с помощью которых обучающиеся могут проверить правильность своих действий и результатов вычислений.

ЛАБОРАТОРНАЯ РАБОТА № 1 ПЕРВИЧНАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ПРЯМЫХ МНОГОКРАТНЫХ ИЗМЕРЕНИЙ /вычисление основных статистических параметров/

1. Цель работы

Освоить основные приемы статистической обработки данных многократных измерений на примере результатов математического эксперимента.

2. Задание

Используя возможности электронных таблиц Excel, получить выборку из нормального распределения. Оценить по выборке значения математического ожидания и среднеквадратического отклонения (СКО) генеральной совокупности, из которой извлечена выборка.

3. Краткая теория

Прямыми называются измерения, при которых искомое значение физической величины получают непосредственно с отчетного устройства средства измерения [2, 3]. Многократными называют измерения физической величины постоянного размера, повторенные несколько раз (не менее 4) при неизменных условиях. Задача состоит в том, чтобы найти оценку неизвестного истинного значения измеряемой физической величины. Обработка результатов многократных измерений производится методами математической статистики, где нет понятия «истинное значение», а используется понятие «математическое ожидание» как среднее значение по всей генеральной совокупности случайной величины. Однако для прямых измерений эти понятия оказываются адекватными, если ошибки измерений случайны и центрированы (имеют нулевое математическое ожидание).

Результаты измерений являются случайными величинами, то есть принимающими в зависимости от случая те или иные значения, заранее неизвестные и непредсказуемые. Каждое отдельное значение непрерывной случайной величины обладает нулевой вероятностью. Однако, нахождение возможных значений случайной величины в различных интервалах обладает различными и отличными от нуля вероятностями. Таким образом, для случайной величины можно определить закон распределения как функцию распределения случайной величины.

Функцией распределения случайной величины (интегральной функцией распределения) называется функция , задающая вероятность того, что случайная величина принимает значение, меньшее , т.е.

. (1.1)

Кроме того, непрерывную случайную величину можно задать дифференциальной функцией распределения или плотностью распределения, которая позволяет дать представление о характере распределения случайной величины в небольшой окрестности некоторой точки числовой оси.

. (1.2)

График дифференциальной функции распределения называется кривой распределения. Кривая распределения, выражающая общую закономерность данного типа распределения, называется теоретической кривой распределения.

В статистике широко используются различные виды теоретических распределений, каждое из которых имеет специфику и свою область применения. Чаще всего в качестве теоретического распределения используется нормальное распределение¹, имеющее уравнение для плотности распределения

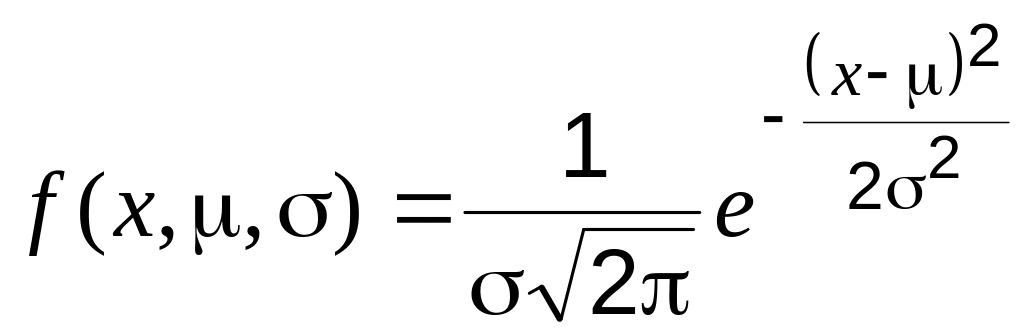, (1.3)

а уравнение интегральной функции распределения –

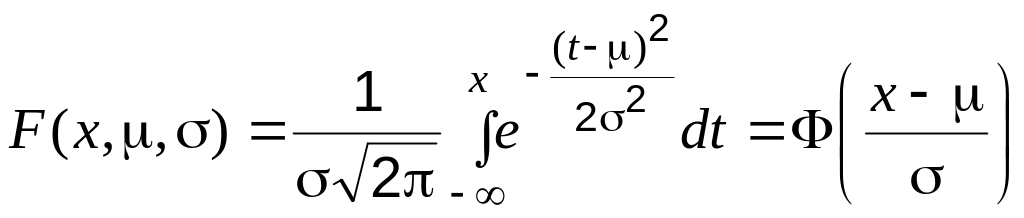, (1.4)

где – математическое ожидание случайной величины , – ее дисперсия, а – среднеквадратическое отклонение.

Параметры (числовые характеристики) закона распределения обычно остаются неизвестными. По выборке могут быть найдены лишь их оценки.

При многократных измерениях за результат измерений обычно принимается среднее арифметическое (СА):

. (1.5)

Иногда вместо СА используют выборочную медиану, которую при нечетном числе измерений находят по формуле:

, (1.6)

а при четном – по формуле:

, (1.7)

причем предварительно результаты измерений располагают в неубывающем порядке: . Такой порядок значений составляет вариационный ряд.

Реже используется выборочная мода как значение, соответствующее максимуму гистограммы (см. лаб. работу «Построение гистограммы…»).

Все эти оценки определяются по выборке и выражаются одним числом, то есть точкой на числовой оси, и называются точечными выборочными оценками математического ожидания (истинного значения физической величины).

Важными характеристиками точечных оценок являются следующие:

• несмещенность. Оценка (например, 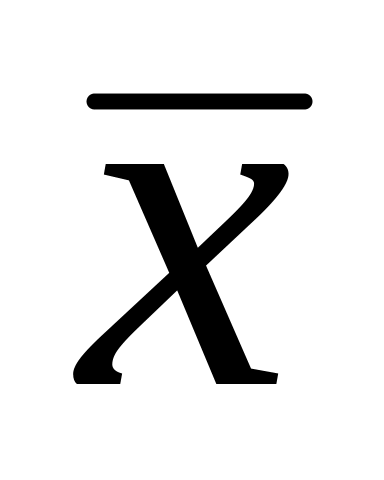) параметра (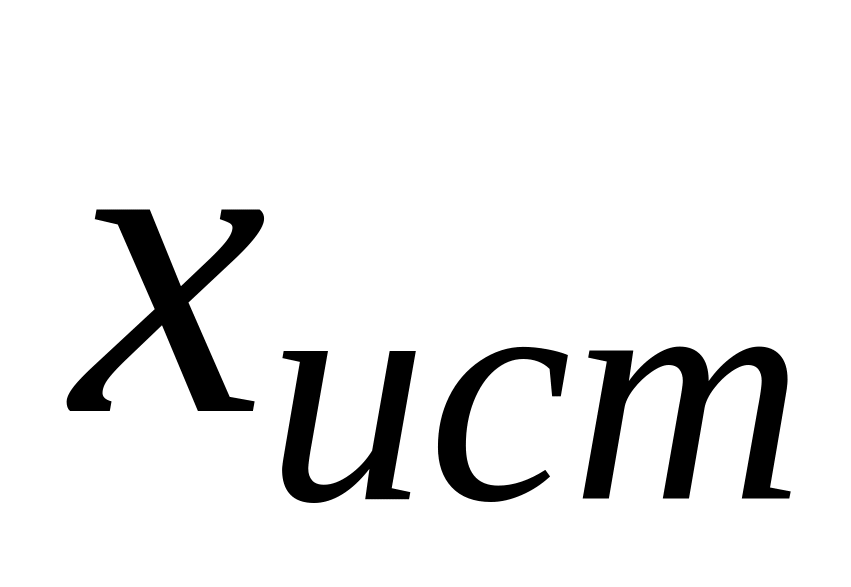 ) называется несмещенной, если ее математическое ожидание совпадает с оцениваемым параметром;

• состоятельность. Оценка называется состоятельной, если с увеличением объема выборки (число измерений) вероятность того, что оценка сходится к истинному значению, стремится к 1.

• эффективность. Оценка называется эффективной, если она обладает минимальной дисперсией по сравнению с другими оценками¹.

Чаще всего используется среднее арифметическое. Оно обладает следующими преимуществами перед другими оценками:

1. при любом законе распределения ошибок (с конечными математическим ожиданием и дисперсией) СА является несмещенной и состоятельной оценкой математического ожидания;

2. дисперсия СА в 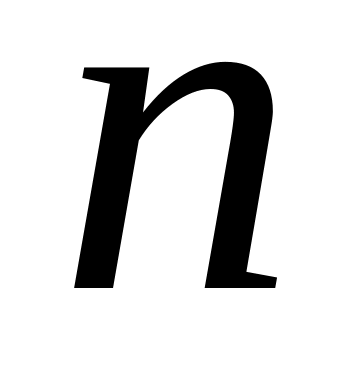раз меньше дисперсии отдельных результатов измерений, то есть дисперсии ошибок;

3. в случае нормального распределения ошибок измерений СА является эффективной оценкой математического ожидания;

4. в случае нормального распределения ошибок измерений СА распределено нормально, а при других распределениях ошибок – асимптотически нормально. Причем с увеличением объема выборки распределение СА быстро сходится к нормальному.

Недостатком СА является то, что оно весьма чувствительно к промахам (грубым ошибкам).

Найденное по выборке случайных величин СА , является случайной величиной. Разность между ним и неизвестным истинным значением называется в статистике ошибкой, а в метрологии погрешностью. Она остается неизвестной и также является случайной величиной.

При неизвестной дисперсии (и неизвестном математическом ожидании или истинном значении , если ошибки центрированы) ее точечной несмещенной и состоятельной, а при нормальном распределении ошибок и эффективной оценкой, является выборочная оценка дисперсии:

. (1.8)

Для вычисления оценки среднеквадратического отклонения по выборке обычно пользуются формулой:

. (1.9)

Для оценки среднеквадратического отклонения среднего арифметического пользуемся формулой, полученной из выражения (1.9) и свойства 2 среднего арифметического:

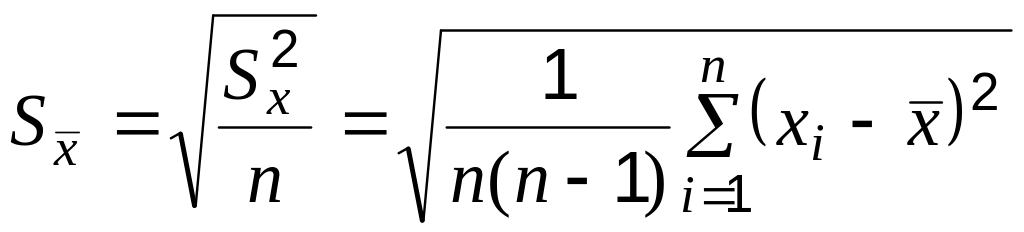. (1.10)

Более подробные теоретические сведения см. в [4,5].

В работе предлагается выполнить расчеты двумя способами: с помощью аппарата статистических функций, а также используя надстройку Excel Пакет анализа. Последовательность установки и основы работы с Пакетом анализа смотри в прил. 1.