
- •3. Визначники 2–го порядку та їх властивості.
- •Доведення:
- •6Означення визначника n-го порядку
- •7Властивості визначників n-го порядку
- •8Поняття вектора.Лінійні дії над векторами.
- •11 Декартова система координат
- •12Скалярний добуток векторів
- •13Векторний добуток векторів
- •14. Мішаний добуток трьох векторів.
- •21. Взаємне розташув 2 площ. Кут між прямою і площиною
- •22. Канонічне рівняння еліпса, його геометричні властивості.
- •27 Множення матриць
- •28 Елементарні перетворення матриць
- •32. Компл числа. Тригонометрична форма комплексного числа
- •33. Дії над компл. Числами. Ф-ла Муавра
- •34. Операції над многочленами.
- •35. Корені многочленів. Теорема Безу. Метод Горнера
- •36 Основна теорема алгебри
- •37. Раціональні дроби
- •38.Аксіоматичне визначення векторного простору
- •40.Підпростори векторного простору
- •41.Афінний простір...
- •42.Ранг матриці.
- •43.Підпр, утвор ровязк однор слр
- •44 Неоднор системи лінійних рівнянь. Теорема Кронекера-Капеллі
- •45.Лп та їх матриці. Дії над лп. Обернене лп.
- •46.Матриці лп. Подібні матриці.
- •47.Характеристичний многочл, власні числа і власні вектори лп
- •48. Означ евклід прост. Ортог вектори. Ортогоналізація Гр-Шмі.
- •49.Ортонормовані базиси і ортогональні матриці.
- •50.Ортогональні перетворення.
- •51 Означення квадратичних форм(кф). Основні ознаки додатної визначеності.
- •52 Зведення кф до канонічного вигляду
- •53) Поняття множини. Рівність множин.
- •54) Операції над множинами.
- •55) Означення функції. Види відображень.
- •56. Складена, обернена функція.
- •57. Параметричне та неявне відображення.
- •58. Аксіоми множин дійсних чисел
- •59. Розширення множини дійсних чисел
- •60. Основні характеристики дійсного числа.
- •61. Обмежені та необмежені числові множини.
- •62. Верхня та нижня межа множини.
- •63 Принцип Архімеда.
- •64. Принцип вкладених відрізків
- •65) Еквівалентність множин та поняття потужності
- •66) Зчисленна потужність
- •67) Континуальна потужність
63 Принцип Архімеда.
Т.
Для б-якого a
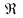 існує n
натуральне(n>0).
існує n
натуральне(n>0).
Дов(від
супротиіного). Нехай
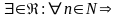 обмежена
зверху
обмежена
зверху
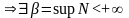 .
Скористаємося означенням sup
. Виберемо
.
Скористаємося означенням sup
. Виберемо
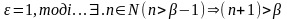 --суперечність.
--суперечність.
Наслідок—
принцип
Архімеда: Для
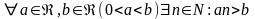 .
Для доведення в Т. Взяти замість а—b/a.
.
Для доведення в Т. Взяти замість а—b/a.
64. Принцип вкладених відрізків
Озн
1: Сист числ
відр [a1,b1],
[a2,b2]…
[an,bn],наз
сист вкладених відрізків(СВВ), якщо
a1<=a2<=…<=an<=bn<=…<=b2<=b1,
тобто
[an,bn]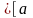 n+1;bn+1],
n+1;bn+1],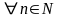
Теорема. Б-яка СВВ має непор переріз .
A={an, n N}—множина лівих кінц відр
B={bn, n N}—правих
Для б-якого нат m,n з озн СВВ вик am<=bn. За аксіомою непервності множ дійсних чтсел
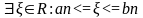 .
.
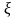 нал всім відр, тому їх переріз непорожній.
нал всім відр, тому їх переріз непорожній.
Озн
Сист
відр [an;bn]
, n—натуральне,
називається системою стяжних відрізків,
якщо довжини цих відрізків (bn-an) 0,
коли
0,
коли
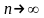
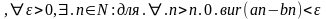 .
.
Принцип
вкладених відрізків. Для
б-якої СВВ існ єдина точка
, що
нал всім відр сиситеми, при чому
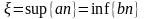
Дов :З теореми випливає, що переріз всіх відр непорохній. Доведемо, що цей переріз скл з єдиної точки (від супротивного).
Нехай,
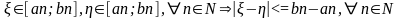 .
За означенням стяжних відр
.
За означенням стяжних відр
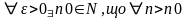 вик
вик
(bn-an)<
. Виберемо
=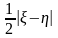 ,
тоді
,
тоді
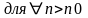 маємо
співвідн
маємо
співвідн
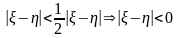 --суперечність.
Отже
--єдина.
--суперечність.
Отже
--єдина.
Зауваження an<=sup{an}<= <=inf{bn}<=bn, для б-якогог нат n. В силу єдиності маємо sup{an}=inf{bn}= .
Якщо
замість відр розгл інтервали або
пііввідрізки, то заданий принцмп не має
місця
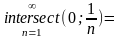 пуста
множина
пуста
множина
65) Еквівалентність множин та поняття потужності
Озн: множини А і В називаються еквівалентними, якщо існує бієктивне відображення з А в В ( f:A B) Позн: А~B
Властивості еквівалентних множин 1)A~A (рефлективність)
2) A~B => B~A (симетричність)
3) A~B B~C => A~C (транзитність)
4)
Ai~Bi
, i
L
, Ai
Aj =
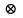 , Bi
Bj
0 , i
j
=> UAi~Ubi
, Bi
Bj
0 , i
j
=> UAi~Ubi
Спираючись на властивість еквів-сті множин можна розподілити всі мн-ни по класам еквівал-сті.Такі різні класи не перетинаються між собою.
Множини
одного класу еквівалентності називаються
рівнопотужними.
Кожній
множині з класу еквівалентності
приписують число, що наз потужністю і
позначається
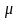 (A)
, де А – представник класу еквівал-сті.
(A)
, де А – представник класу еквівал-сті.
Озн: Множина А наз скінченною, якщо n N| , що А ~{1,2,…,n} причому n наз числом елементів множини А.
Порожня множина – скінченна, а ( )=0
Теорема: 2 скінченні множини еквівалентні ( рівні) тоді і тільки тоді, коли вони мають однакову кількість елементів.
Озн: Якщо множина не є скінченною , то вона наз нескінченною.
Приклад: множина парних натуральних чисел рівнопотужна множині натуральних чисел.
Між елементами існує бієкція
f
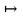 2n
, n
N|
2n
, n
N|множина цілих чисел рівнопотужна множині цілих чисел Z~N 2n n, n=1,2,… 2n+1 -n , n=0,1,2…
будь-які 2 скінченні інтервали ( відрізки) рівнопотужні [a,b]~[c,d] , a,b,c,d R , a<b , c<d (x-a)/(b-a)=(y-c)/(d-c) ; y= c+ (d-c)(x-a)/(b-a)
множина дійсних чисел рівнопотужна будь-якому скінченному інтервалу R~(a,b). З приклада 3 (a,b)~(c,d)~(0,1) встановимо бієкцію між (0,1) і R f: (0,1)->R f(x)=ctgПx
x R f:N->X f(n)=xn X , кажуть ,що задана числова послідовність, причому xn- центральний член послідовності, який набуває значення з множини Х. {xn,n N} Послідовність еквівалентна N,тобто нескінченна,а значення,які набувають члени послідовності можуть складати скінченну множину (Х-скінченна)
Правила порівняння потужностей
1) (А)= (В) <=> A~B
2) (А)< (B)(A не~B)^( C<B,C~A)
3) (A)< (B) => (B)> (A)
4) (A) (B) ( (A)< (B)) ( (A)= (B))
