48. Означ евклід прост. Ортог вектори. Ортогоналізація Гр-Шмі.

Векторний простір Е наз евклід простором, якщо для век-в цього простору виконані такі вимоги: 1) кожній парі в-вa a,b є Е ставиться у відповідність дійсне число (a,b) , яке наз скалярним добутком a і b.

2) скал добуток задовольняє аксіоми (a,b, с – вектори, λ-число)

1)(a,b) = (b,а) 2) (a+b,с) = (а,с) + (b,с) 3) (λ a,b)= λ(a,b) 4) (а,а)≥0 ↔а=0

Довжина вектора а евк простору Е наз величина |a|=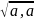 . На підставі аксіоми 4) скал добутку довжина ненульового вектора додатна, а довжина нульового вектора =0. Якщо а є Е, λ-число, то | λ а|=| λ ||а|.

Вектор, довжина якого = 1, наз нормованим. Якщо а є Е, а ≠ 0, то вектор 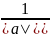а є нормованим і познач .

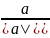Для будь якого вектора a,b є Е викон нерівність Коші-Буняковського:

(a,b)²≤(а,а)(b,b), причому рівність має місце тоді і тільки тоді, коли вектори а і b лінійно залежні.

Кут між векторами а, b є Е наз кут φ, φє[о,П], що виконується рівність:

cosφ= .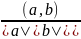

Вектори а, b є Е наз ортогональними (а┴b), якщо їх скал добуток =0.

Система векторів наз ортогональною, якщо або вона скл з одного вектора, або їх вектори попарно ортогональні.

Т. Ортогональна система ненульових векторів є лін незалежною.

Дійсно, припустимо, що вектори а₁, а₂….а_т ненульові і попарно ортогональні. Щоб довести їх лін незалежність, треба показати, що рівність 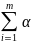_ia_i = 0 модлива лише при виконанні умов а₁= ….=а_т=0.

Помножимо справа обидві частини рівності по черзі на вектори а₁, а₂….а_т, одержимо, що _i (a_i,а_j) = 0, j=1,m. Оскільки (a_j,а_i)≠0 і (a_i,а_j)=0 при i≠j, то α_j=0, j=1,m. Отже, вектори а₁, а₂….а_т лін незалежні.

Ортогоналізація Грама-Шмідта

(перехід від с-ми ЛН векторів до ортогон с-ми векторів)

Теорема: Нехай вектори а1,а2,…,аем ЛН. Тоді можна побудувати ортогон с-му ненульових векторів b1,b2,…,bm, які визначаються за формулою:

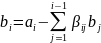i=2,m b1=a1

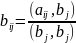
Основні співвідношення векторів:

1)Нерівність трикутника |a+b|<=|a|+|b|

2) Теорема cos: |a-b|²=|a|²+|b|²-2|a||b|cosφ

3) Теорема Піфагора: |a+b|²=|a|²+|b|²(a┴b)

49.Ортонормовані базиси і ортогональні матриці.

Базис е₁,е₂,…е_п евклідова простору Е_n наз ортогональним, якщо вектори цього базису попарно ортогональні. Якщо ж вектори базису, крім того, нормовані, то базис наз ортонормованим. Отже, маємо: e^T_ie_j=δ_ij, де δ_{ij –} символ Кронекера_, δ_ij = .

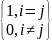Ортонормованим базисом простору Е_n є натуральний базис.

Знайдемо вираз для скалярного добутку довільних векторів a і b, через їх координати відносно ортонормованого базису. Нехай a,b є Е_n, е₁,е₂,…е_п - ортонорм-ий базис та а=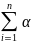 _ie_i, b = 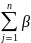_je_j, тоді на підставі аксіом скалярного добутку і рівності e^T_ie_j=δ_ij, маємо:

а^Т b= _ie_i)^Т( _je_j)=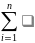 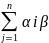_je_і^Те_j= 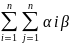_j δ_ij= _iβ_i

Зясуємо, як треба тлумачити коор-ти век-ра а відносно ортонормованог базису е₁,е₂,…е_п . Очевидно, що а^Те_j = _ie_i^Te_j= _iδ_ij = α_j, j= .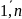

Це означає, що коор-ти довільного вектора відносно ортонормованого базису = скалярним добуткам цтого вектора на відпов базис вектори.

Матриця Q наз ортогональною, якщо Q^т Q=Е. Зауважимо, що Q^-1 Q=Е, тому Q^-1 = Q^т та Q Q^т =Е. Отже, матриця перетворення координат при переході від ортонормованого базису є ортогональною матрицею.

Властивості::

Т1.Матриця є ортогональною тоді, і тільки тоді, коли її стовпці(рядки) утворюють ортонормовану систему векторів.

Доведеня. є наслідком рівності Q Q^т=Е для рядків, Q^т Q=Е для стовпців.

Т2.Добуток двох ортогональних матриць є ортогонал матрицею. Модуль визначника ортогональної матриці =1.

Нехай Q₁, Q₂- ортом м-ці, тоді згідно з визначенням ортом-сті, маємо:

(Q₁Q₂)^Т Q₁Q₂=Q₂^TQ₁^TQ₁Q₂= Q₂^TQ₂=E. Отже, матриця Q₁Q₂ є ортог-ою.

Т3. Для того, щоб симетрична матриця А була представлена у вигляді А = QΛQ^T, де Q – ортогональна і Λ – діагональна м-ця, необхідно і достатньо, щоб стовпці м-ці Q були ортонормованими власними векторами, відповідними до власних значень – діагонал ел м-ці Λ.