46.Матриці лп. Подібні матриці.

Матриця А= а11 а12…а1ен

а21 а22…а2ен -матриця ЛП А в базисі е1,е2,…,еен

………………….

аен1 аен2 аенен

Позначимо (х1,х2,…,хен)^т і (у1,у2,…,уен)^т – матриці-стовпці корд векторів х,у у базисі е1,е2,…,еен простору R_n

Припустимо, що у=Ах, тоді за означенням ЛП:

у=Ах=А . Звідки у_і= , i=1,n

Отже, (у1,у2,…,уен)^т=А(х1,х2,…,хен)^т – будь-якому ЛП А у вибраному базисі відповідає кв матриця А, при чому j-й ст. матр А склад з корд вектора Аej.

Теорема: Якщо у вектор прост R_n задано базис е1,е2,…,еен та невиродж матрицю А ен-го порядку, то існує єдине ЛП, матриця якого =А у базисі е1,е2,…,еен.

Матриці ЛП у різних базисах:

У просторі R_n є старий базис е1,е2,…,еен і новий е1',е2',…,еен'. Запишемо ЛП у цих базисах: у=Ах; у'=А'х', де х', у' – матриці-стовп з корд векторів х,у в базисі е1',е2',…,еен'; А' – матриця ЛП у цьому базисі. Маємо: x=Qx', y=Qy' тоді y'=Q^-1y=Q^-1Ax=Q^-1AQx'. Отже,

A'=Q^-1AQ(1). А~А'-подібні матриці; перехід від А до А' назив перетвор подібності, якщо має місце формула (1), якщо Q-невиродж, Q – матриця переходу від старого до нового базису.

47.Характеристичний многочл, власні числа і власні вектори лп

Нехай в R_n є ЛП А. ненульовий вектор х є R-власний вектор ЛП А, якщо є таке число λ, що виконується:Ах=λх(1)

λ-власне значення(власне число, характеристич число) ЛП А, що відповідає власному вектору х.

Якщо ЛП А задано своєю матрицею А у базисі е1,е2,…,еен, то умову (1) можна представити: (А-λЕ)х=0(2). Якщо хне=0 то (2) має ненульові розвязки, якщо (А-λЕ)=0, тобто det(A-λE)=0 – характеристичне р-ня матриці А.

Можна записати det A=a0+a1λ+…+an-1λ^n-1+λⁿ

Спектр матриці А – множина з n власних значень матриці n-го порядку (кожне власне знач береться стільки разів, яка його кратність).

Властивості х і λ:

1)Слідом trA матриці А n-го порядку назив сума діагональних елем матриці trA=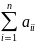

І. Добуток власних значень матр=її визначнику, а сума-сліду

ІІ. А: х і λ

(А+μ): λ+μ; х

ІІІ. А^m - λ^m, x mє Z (невироджена)

• λ^m, x m єN(вироджена)

ІV. Власні вектори, відповід до різних вл знач є ЛН

V.Подібні матриці мають однакові характеристичні многочл:

det (A'-λE)=det(Q^-1AQ-λQ^-1EQ)=det(Q^-1(A-λE)Q)=detQ^-1det(A-λE)detQ=det(A-λE)

Наслідок: хар-ний многочл ЛП не залеж від вибору базису.

Матриця А n-го порядку назив матрицею простої структури, якщо вона має n ЛН векторів.

Теорема: Матриця має просту структуру, коли вона подібна до діагональної матриці.

Нехай А має ЛН власні вектори х1,х2,..,хен відповідні до власних значень λ1,λ2,…,λен, тобто Ax_i=λ_ix_i i=1,n(3)

Нехай Λ=diag(λ1,λ2,…,λn) i S=(x1,x2,…,xn), тоді (3) можна записати у вигляді матричної рівності AS=SA, звідки A=SΛS^-1(4)

Отже, матриці A i Λ – подібні.

Представлення матриці у вигл (4) назив діагоналізац за доп перетвор подібності, а матр S назив діагоналізуюч.

Матриця, всі корені хар-го многочлена якої є простими має ен ЛН влас векторів і тому є матрицею простої структури.

Якщо хар многочл має вл знач кратності k(k>1), то цьому знач можуть відпов менше ніж k ЛН вл векторів. Такі матр-ДЕФЕКТНІ. Деф матр не може бути діагоналізованою.