41.Афінний простір...

Множина Sn наз. n-вимірним аф простором, а її елементи – точками цього прост, якщо кожній впорядк парі елем А,В є Sn став. у відповід єдиний вектор з Rn (вектор АВ є Rn) так, що мають місце аксіоми:

А1. Для кожної т.А, що є Sn, кожного вектора а є Rn існує єдина точка В, що є Sn така, що АВ=а

А2. Для будь-яких трьох точок А,В,С є Sn виконується АВ+ВС=АС

Заув. Вект. простір Rn є Афінним простором. За т. простору Sn беруться вектори Rn. А->а, В->в, АВ->в-а Навпаки, кожний Аф. простір Sn є арифметичним, оск. якщо обрати початок т. О, що є Sn та утворити радіус-вектори ОА і ОВ, то ці вектори будуть елементами Rn.

Введемо Аф сист. коорд (АСК). Для цього зафікс довж. т. О є Sn (поч коорд.) та в просторі Rn вибираємо деякий базис. Rn: е1, е2,..., еn. Виберемо довж. т. М є Sn. Побуд. вектор ОМ=х(радіус-вектор) є Rn.

Р озкл х в Rn за базисом:ОМ=α₁е₁+α₂е₂+...+α_ne_n, коеф. α_і – коор.т.М в АСК.

MN=ON-OM=(β₁ – α₁)е₁+(β₂ – α₂)е₂+...+(β_n – α_n)е_n, де β_і – афінні коорд. т. N, α_i – т.M

Якщо в Аф. просторі Sn зафікс т. А, А є Sn; в ариф прост. вибрано підпростір Um (Um є Rn), то множина всіх точок афінного прост М є Sn таких, що АМ є Um, назив. m-вимір площ, що прох. через т.А в напр підпрост Um. А-початк. точка, М-поточна т.,Um-напр підпростір.

Um: m=0,то нульвимірна площина – т. А; m=1, то площ. назив. прямою лінією; m=n-1, то площ. наз. гіперплощ; m=n, то m-вимір площ збіг з Sn.

С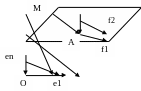 кладемо р-ня m-вимірної площини. Розглянемо АСК: 0,е₁,...,е_n. m-вимірна площина: А є Sn, Um с Rn, Um: f₁,f₂,…,f_m. OA=f₀, AM є Um, ОМ=х.

ОМ=ОА+АМ.

x=f₀+ (1) (розклад за базисом Um) – векторне р-ня m-вимірної площини α_і є R, і=1,м Перейдемо до координатної форми векторів:

f_i=(f_i1, f_i2,…, f_in)^T, i=0,m (належить Rn)

х=(х₁,...,х_n)^T Отже, x_j=f_0j+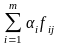 , j=1,n (2) – параметр р-ня m-вимір площ. Якщо f₀=θ, то m-вимір площ. збіг з Um (р-ня (1) або (2) зад. підпр Um)

Векторне р-ня прямої(m=1): А, f₀, f₁; х=f₀+α₁f₁;

Парам. р-ня: х_j=f_0j+α₁f_1j, j=1,n

Канонічне: α₁=(х₁- f₀₁)/ f₁₁=(х₂- f₀₂)/ f₁₂=(х_n- f_0n)/ f_1n

42.Ранг матриці.

Нехай є матр. А mxn . Будемо розглядати рядки матр. як n-вимірні вектори простору Rn, а стовпці – як m-вимірні вектори простору Rm. Можна вивчати лінійну залежність і незал. рядків або стовпців матр. А.

О.Мінором і-го порядку матр. А назив. визначник і-го порядку з елем, розміщеними на перетині будь-яких і-рядків та і-стовпців матр. А.

Рангом матр. А наз. максим порядок відмінних від нуля мінорів матриці і позн. r(A) або rang(A); r(θ) = 0; 0≤r(A)≤min{m,n}

Будь-який мінор, що≠0 порядку r(A) назив. базисним мінором, а стовпці і рядки, в яких він розміщ., назив. базисними.

Теорема:Базисні стовпці(рядки) матриці лін незал та б-який стов (ряд) є лін. комбінацією базисних стовпців(рядків).

Висновок1:вимірність підпростору, породженого деякою сист. векторів = рангу матриці, складеної з коорд. цих векторів відносно деякого базису.

Висн.2: Максим. к-сть лін. незалежних стовпців(рядків) матриці = рангу матриці

Теорема: Для того, щоб визначник матр. А порядку n=0, необх. і достатньо, щоб його стовпці(рядки) були ліню залежними.

Для знах. рангу матриці зручно звести її елементарн. перетвор. з рядками до так званої ступінчастої матриці. Ця матриця має таку будову: 1)ненульові рядки розм. вище нульових,2)кожний провідний елемент, який є першим ненульовим елем. в своєму рядку(рахуючи зліва направо)=1, 3)кожний провідн. елемент розміщ. праворуч від провідного елем. попереднього рядка.

G-ступінчаста матриця. G=LA, L-добуток елементарних матриць. r(G)= r(LA)= r(A)

Теорема: Для mxn матр. А рангу r існують такі невироджені матриці L і M порядків m і nвідповідно, що LAM=

Теорема: Ранг добутку двох матриць не перевищує рангу кожного з множників r(АВ)≤r(A); r(АВ)≤r(В). Д-ня: розглянемо блокову матрицю (АВ А) : r(АВ)≤r(AВ А)≤r(А), де АВ-лін. комбінація стовпців матр. А.

Наслідок: множення матриці на невиродж. матр. не змінює її ранг. Д-ня:

r(А)=r(AВВ^-1)≤r(АВ)≤r(A) => r(А)=r(AВ), В-невиродж.