1. Основні поняття лінійної алгебри. Системи лінійних рівнянь.

2. Метод Гаусса розв’язання систем лінійних рівнянь.

3. Визначники ІІ порядку, їх властивості.

4. Визначники ІІІ порядку. Алгебраїчні доповнення та мінори. Формула Лапласа.

5. Формули Крамера для систем лінійних алгебраїчних рівнянь II і III порядків.

6. Означення визначника n-го порядку.

7. Властивості визначників n-го порядку.

8. Поняття вектора. Лінійні дії над векторами.

9. Лінійно незалежні системи векторів. Базис, розклад вектора за базисом.

10. Проекція вектора на вісь.

11. Декартова система координат у просторі. Координатна форма вектора.

12. Скалярний добуток векторів та його властивості.

13. Векторний добуток векторів.

14. Мішаний добуток трьох векторів.

15. Векторне і нормальне рівняння площини.

16. Загальне рівняння площини. Відстань та відхилення точки від площини.

17. Кут між двома площинами.

18. Пряма на площині. Кут між прямими.

19. Різні види рівнянь прямої в просторі.

20. Кут між прямими в просторі, умова належності двох прямих одній площині.

21. Взаємне розташування двох площин. Кут між прямою і площиною.

22. Канонічне рівняння еліпса, його геометричні властивості.

23. Канонічне рівняння гіперболи, її геометричні властивості.

24. Канонічне рівняння та параболи, її геометричні властивості.

25. Загальне рівняння кривої другого порядку.

26. Види матриць. Лінійні операції над матрицями.

27. Множення матриць.

28. Елементарні перетворення матриць.

29. Обернена матриця.

30. Блокові матриці.

31. Розв’язування матричних рівнянь.

32. Комплексні числа. Тригонометрична форма комплексного числа.

33. Дії над комплексними числами. Формула Муавра.

34. Операції над многочленами. Найбільший спільний дільник.

35. Корені многочленів. Теорема Безу. Метод Горнера.

36. Основна теорема алгебри.

37. Розклад раціональних дробів.

38. Аксіоматичне визначення векторного простору.

39. Вимірність і базис векторного простору. Перетворення координат при переході до нового базису.

40. Підпростори векторного простору.

41. Афінний простір. Площини і прямі в афінному просторі.

42. Ранг матриці, його обчислення.

43. Підпростір, утворений розв’язками однорідної системи лінійних рівнянь. Фундаментальна система розв’язків.

44. Неоднорідні системи лінійних рівнянь Теорема Кронекера-Капеллі.

45. Лінійні перетворення та їх матриці. Дії над лінійними перетвореннями. Обернене лінійне перетворення.

46. Матриці лінійного перетворення. Подібні матриці.

47. Характеристичний многочлен, власні числа і власні вектори лінійного перетворення.

48. Означення евклідового простору. Ортогональні вектори. Ортогоналізація Грама-Шмідта.

49. Ортонормовані базиси і ортогональні матриці.

50. Ортогональні перетворення.

51. Означення квадратичної форми. Основні ознаки додатної визначеності.

52. Приведення квадратичної форми до канонічного вигляду.

53. . Поняття множини. Рівність множин.

54. Операції над множинами.

55. Означення функції. Види відображень.

56. Складена функція, обернена функція.

57. Параметричне та неявне відображення.

58. Аксіоми множини дійсних чисел.

59. Розширення множини дійсних чисел.

60. Основні характеристики дійсного числа.

61. Обмежені та необмежені числові множини.

62. Верхня та нижня межі множини.

63. Принцип Архімеда.

64. Принцип вкладених відрізків.

65. Еквівалентність множин та поняття потужності.

66. Зчисленна потужність.

67. Континуальна потужність.

1.Системою лінійних рівнянь- розмірів mxn наз. с-ма m лін р-нь з n невід вигляду (1)

де х , =

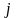Коефіцієнти при невідомому утв. прямокутну таблицю, яка наз. матрицею розміру m n

якщо m=n, то матриця наз. квадр. порядку n.Елем цієї матр (а₁₁,…,а_nn) утв гол діаг матр

Одинична матриця- квадр. матр. на головній діагоналі якої стоять 1 решта елем. =0.

Змінні і вільні члени можна пред. у вигляді таких матриць

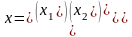
Розв’язок СЛР(1)- наз. така сукупність чисел , які перетворюють кожне з рівнянь системи в числову тотожність.

Якщо СЛР має розв.- наз. сумісною, якщо ні- то несумісна.

Якщо СЛР має єдиний розв’язок- визначена, якщо більше- невизначена.

Зауваження:

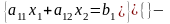другого порядку

Дві СЛР наз. еквівалентними, якщо ці системи мають одну й ту саму множ. розв’яз. або вони одночасно несумісні.

Елементарні перетворення СЛР-такі перетворення + до обох частин деякого рівняння с-ми іншого рівняння множ. на деяке число;переставл двох будь-яких р-нь;множення деякого р-ня на число, яке не =0;видалення з сист. рівняння вигляду 0=0.

Доведення: Нехай до 2-го рів-ня додали 1-ше помнож. на . Утв. нове рівняння. Нехай 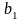L = ,L 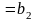-два рівняння початкової системи. Рівняння L замінимо на . Якщо прав. рівності і L поч.. с-ми, то викон. рівності L = і . навпаки, якщо викон. рівності L = і перетворення с-ми, то правильні рівності L = і L -початков.

2.Метод Гаусса- це спосіб роз. СЛР, що полягає у перетворенні с-ми, у таку еквіваленту, розв. якої знаходь. досить легко.

Нехай в СЛР (1)

Якщо , то шукаємо а з номером і1, де і не = 0.

Послідовно домножуємо 1 р-ня на /а₁₁, і=2,m і віднім від і-го р-ня . одержимо еквівалентну систему.

Якщо виникла ситуація а)0=0-виключаємо б)0=λ, λне=0-несуміс с-ма.

Застосовуємо аналогічні дії для вилуч. змінної спираючись на 2-ге рівняння .

Якщо СЛР сумісна, то метод Гаусса дасть такий результат:

де 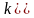, якщо було р-ня 0=0); (якщо k=n, то сис-ма визначена, бо з останнього р-ня можна знайти ), а потім знайти решту змінних.

Якщо , то система невизначена, та 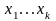змінних знайдемо через вільних змінних, тобто безліч розв’язків.

Висновок: метод Гауса можна застос. для розв. будь- якої СЛР і знайти всі розв с-ми, якщо вона сумісна.

СЛР наз. однорідною, якщо всі вільні члени=0, інакше вони наз. неоднорідними.

Однорідна с-ма завжди сумісна(є нульвий розв'язок).

3. Визначники 2–го порядку та їх властивості.

Означення :

Визначником(детермінантом) 2–го порядку назив число(алгебр вираз), що визначається за таким правилом :

а₁₁ а₁₂

∆=│ а₂₁ а₂₂ │= а_11*а₂₂-а_12*а₂₁

Властивості визначників 2-го порядку:

1.значення визначника не зміниться при його транспортуванні ( при заміні рядків відповідними стовпчиками і навпаки):

а₁₁ а₂₁

∆^т =│ а₁₂ а₂₂│

∆ = ∆^тНаслідок : рядки та ст визначн рівноправ, отже всі власт, які мають місце для рядків, вірні і для стовпців.

2.при переставленні двох сусідніх рядків (стовпців) визначник змінює знак на протилежний:

∆^{' = |}а₂₁ а_22| = (а_21*а₁₂ – а_11* а₂₂) = –∆

_|а₁₁ а_12|

3.спіл множн всіх ел деяк рядка(стовпця)можна винести за знак визн :

∆ = λа₁₁ λ_{12 =} λа₁₁а₂₂ – λа₁₂а₂₁ = λ(а₁₁а₂₂ - а₁₂а₂₁ ) = λ ∆

а₂₁ а₂₂

4.якщо у визначнику всі елем деяк рядка( стовпця)є сумами 2 доданків, то цей визн = сумі двох визн, що відрізн від заданого вибраним рядком, а саме : у перш цей рядок скл з перших доданків, а у другого – з других.

∆ = а¹₁₁+а¹¹₁₁ а¹₁₂+а¹¹₁₂ =а_22* ( а^'₁₁ + а^''₁₁) – а_21* (а^'₁₂ + а^''₁₂)

а₂₁ а₂₂

∆ = а^'₁₁+а^''₁₁ а^'₁₂+а^''₁₂ = а^'₁₁а^'₁₂ + а^''₁₁ а^''₁₂ = а₂₂

а₂₁ а₂₂ а₂₁ а₂₂ а₂₁ а₂₂

(а^'₁₁ + а^''₁₁) – а₂₁ ( а^'₁₂ + а^''₁₂)

5.визначник = нулю при виконанні однієї з наступних умов:

1)всі елементи деякого рядка (стовпця) дорівнюють нулю;

2)всі елем деякого рядка(ст) пропорц відповід елем іншого рядка ( ст.)

∆ = а в = 2ав-2ав = 0

2а 2в

3)якщо є два однакових рядки ( стовпці)

∆ = а в = ав – ав =0

а в

6.визн не змін свого знач, якщо до елем деяк рядка ( ст.) додати відповідні елементи іншого рядка ( ст. ), домноженого на деяке число.

а₁₁ а₁₂+λа₁₁ а₁₁ а₁₂ а₁₁ λа₁₁ а₁₁ а₁₁

а₂₁ а₂₂+λа₂₁ = а₂₁ а₂₂ + а₂₁ λа₂₁ = ∆ + λ│а₂₁ а₂₁│= ∆

4.Визн 3-го порядку. Алгебр доповн та мінори. Ф-ла Лапласа. Означення :Визначником( детермінантом) 3-го порядку називається число ( алгебраїчний вираз ), що визначається за правилом

а₁₁ а₁₂ а₁₃

∆ = а₂₁ а₂₂ а₂₃ = а₁₁а₂₂а₃₃+а₁₂а₂₃а₃₁₊а₂₁а₃₂а₁₃-а₃₁а₂₂а₁₃-а₂₁а₁₂а₃₃- а₁₁а₃₂а₂₃

а₃₁ а₃₂ а₃₃

Зауваж: означ визн 3-го пор випис за допомогою правила трикутників.

Зауваження : визначник можна обчислити за правилом Сарюса:

а₁₁ а₁₂ а₁₃ а₁₁ а₁₂

а₂₁ а₂₂ а₂₃ а₂₁ а₂₂

а₃₁ а₃₂ а₃₃ а₃₁ а₃₂

Властивості 1-6 визначника 2-го порядку мають місце і для визначника 3-го порядку.

О.Мінором (М_{i j}) i,j=1,3 визначника ∆, що відповідає елементу а_{i j} цього визначника, називається визначник 2-го порядку, одерж з визначника ∆ викресленням і-го рядка і j-го стовпця, на перетині яких стоїть а_{і j.}

а₁₁ а₁₂ а₁₃ а₂₁ а₂₃

∆₌ а₂₁ а₂₂ а₂₃ М₁₂= а₃₁ а₃₃

а₃₁ а₃₂ а₃₃

О.Алгебраїчним доповненням елемента а_{і j} визначника ∆ називається число ( алгебраїчний вираз ) , що дорівнює А_{i j} = (-1)^i+j_* M_{i j}

7.(формула Лапласа) : визначник = сумі добутків елементів будь-якого рядка (ст.) на відповідні цим елементам алгебраїчні доповнення:

∆ = і= 1,3

∆ =наоборот для і

8: сума добутків елементів будь-якого рядка (ст.) на алгебраїчні доповнення відповідних елементів іншого рядка (ст.) дорівнює нулю.

∆ = а₁₁А₁₁+ а₁₂А₁₂ + а₁₃А₁₃

0=а₁₁А₂₁+а₁₂А₂₂+а₁₃А₂₃

Метод нагромадження нулів – це метод обчислення визначника, що спирається на властивість 6-7 і полягає у послідовному застосуванні властивості 6 з метою утворення в деякому рядку (ст.) певну кількість нулів, а потім застосовується властивість 7.

5.Ф-ла Крамера для СЛР ІІ і ІІІ порядків.

1)Для 2 порядку

=a11 a12 1=|b1 a11| 2 =|b1 a11|

a21 a22 b2 a22 b2 a22

Теорема: Якщо гол визн СЛР 2 пор не=0, то система визначена(1 розв), при чому мають місце ф-ли Крамера

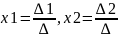
Зауваж: СЛР2 має єдиний розв’язок, якщо 0.

Якщо = 1= 2=0 ,то система має безліч розв’язків

Якщо =0 1 0 ( 2 0) - несумісна