18. Неопределенный интеграл. Таблица интегралов.

Определение: Семейство всех первообразных функции f на отрезке

[ a,b ] называется неопределенным интегралом функции f.

Таблица интегралов.

ln |x| + c

Примеры: 1.

2.

19. Вычисление неопределенного интеграла способом подстановки.

Общая формула: если x= (t), то

1.

[ замена ln x = t, ]

2.

[ замена cos x=t, -sinxdx=dt =>sinxdx=-dt]

20. Определенный интеграл. Формула Ньютона – Лейбница.

Рассмотрим задачу о вычислении площади криволинейной трапеции. Разобьем отрезок [a,b] на n отрезков одинаковой длины

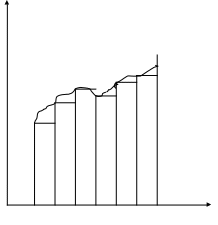точками х₀=а <x₁<x₂<….<x_n=b

и пусть Δх= (к= )

На каждом из отрезков [x_k-1,x_k]

Как на основании построим

прямоугольник высотой f(x_r-1).

Площадь этого прямоугольника

равна

f(x_r-1) x Δx = f(x_r-1), а

сумма площадей всех таких

прямоугольников

S_n= (f(x₀)+f(x₁) +…+f(x_n-1))

а=x₀ х₁ х₂ х₃ х_n-1 x_n= b

В силу непрерывности функции f объединение этих прямоугольников при n почти совпадает с криволинейной трапецией. Число, к которому стремится S_nназывается интегралом функции f от а до в и обозначается

S_n , где а,в – пределы интегрирования.

Вообще, _{= F(b)} – F(a) – формула Ньютона – Лейбница.

21. Применение интеграла.

1. Нахождение площади криволинейной трапеции.

S =

2. Объем тела вращения.

a) Вокруг оси ОХ: V_ox= π

б) Вокруг оси ОУ: V_oу= π

3. Путь, пройденный точкой за время T.

S =

4. Работа переменной силы.

А =