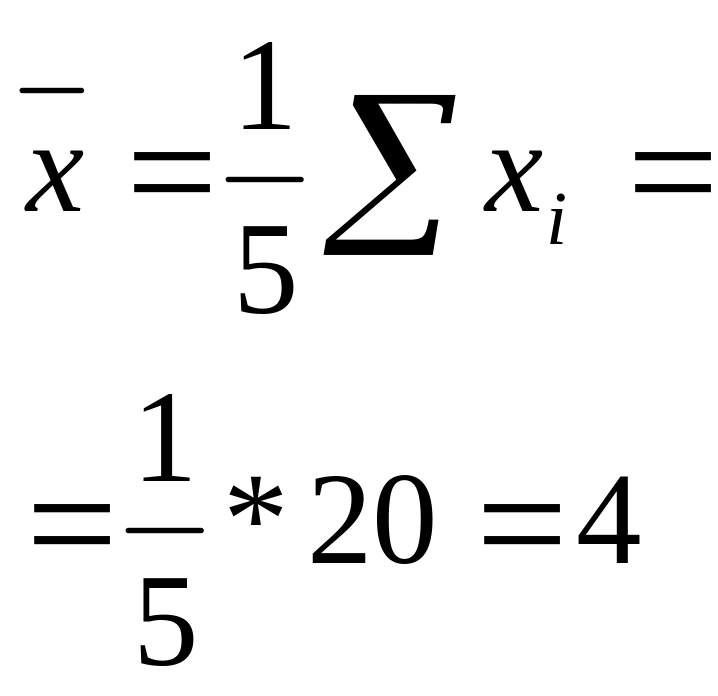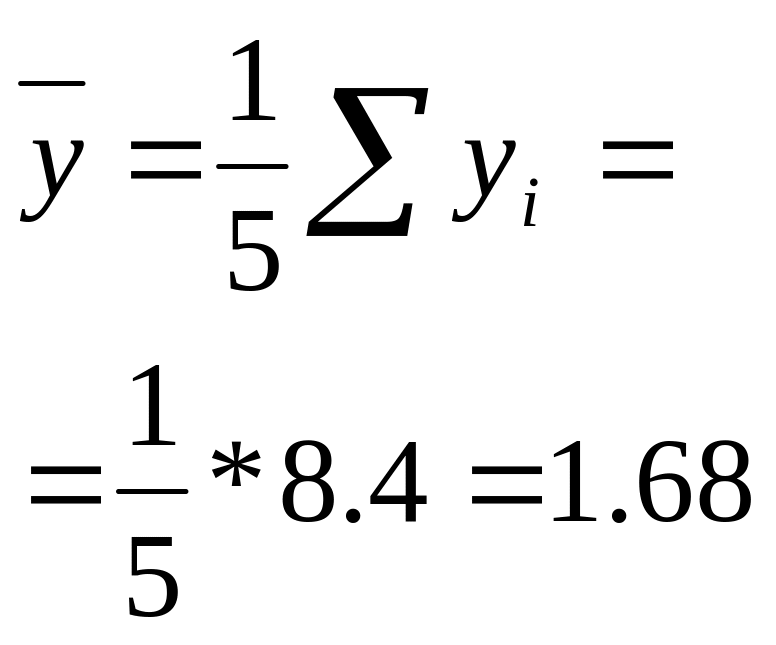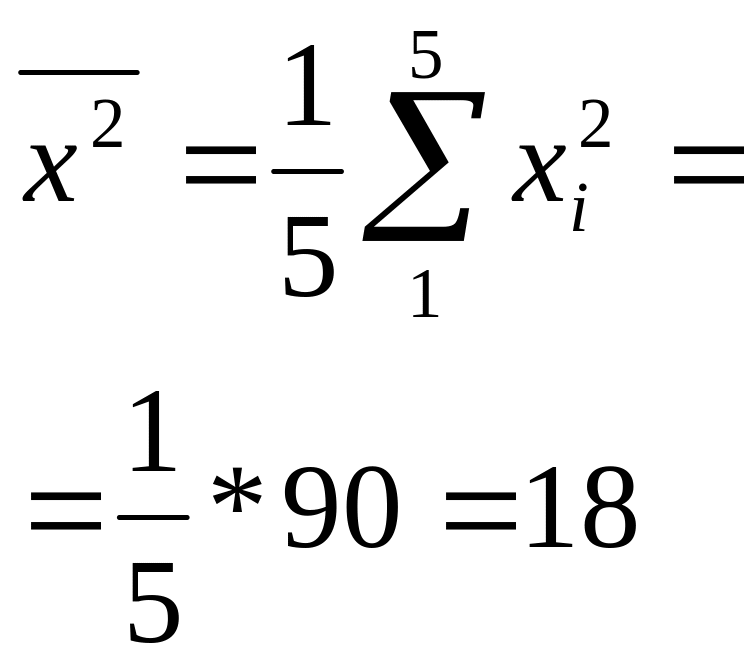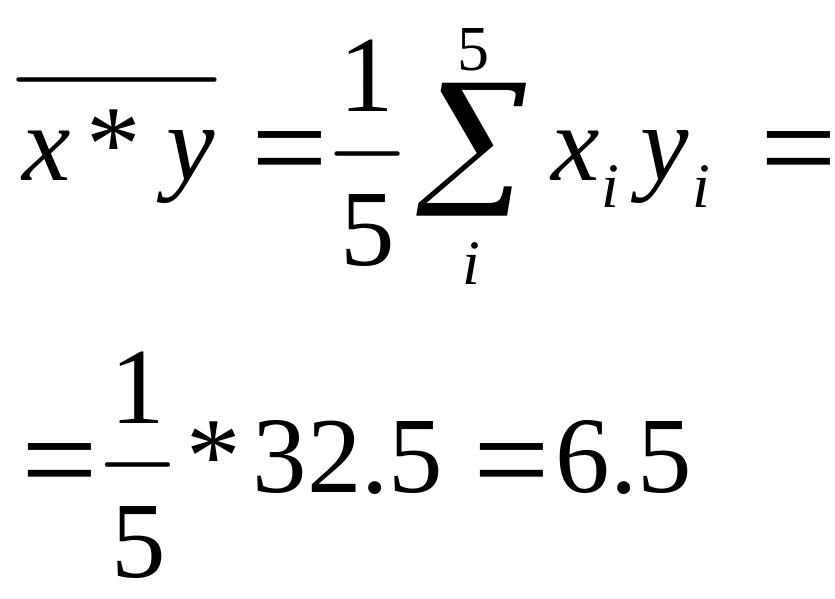4.3 Качество оценки: Коэффициент детерминации

Цель регрессионного анализа состоит в объяснении поведения зависимой переменной .

Пусть на основе выборочных наблюдений построено уравнение регрессии .

Значение зависимой переменной в каждом наблюдении можно разложить на две составляющие , , где остаток есть та часть зависимой переменной , которую невозможно объяснить с помощью уравнения регрессии.

Разброс значений зависимой переменной характеризуется выборочной дисперсией . Разложим :

Так как , то .

Замечание. Такое разложение дисперсии верно лишь в том случае, когда константа а включена в уравенение регрессии.

Итак, дисперсия разложена на две части:

– часть, которая объясняется регрессионным уравнением,

– необъясненная часть.

Разделим правую и левую часть равенства на :

,

TSS=ESS+RSS.

Получим .

Коэффициентом детерминации называется отношение

,

Коэффициентом детерминации и характеризует долю дисперсии (вариации или разброса) зависимой переменной, объясненную с помощью уравнения регрессии.

Максимальное значение .

Это происходит в случае, когда все точки наблюдения лежат на регрессионной прямой (подгонка точная), т.е. и остатки для всех .

Тогда . Если , то регрессия ничего не дает, т.е. .

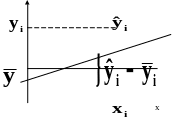
Это значит, что переменная не улучшает качества предсказания по сравнению с горизонтальной прямой (рисунок 4.5).

Рисунок 4.5

Чем ближе к единице , тем лучше качество подгонки, т.е. более точно аппроксимирует .

Замечание. Вычисление корректно, если константа а включена в уравнение регрессии.

Напомню, что выборочные дисперсии и :

дисперсия наблюдаемых значений .

дисперсия расчетных значений

- дисперсия остатков.

Пример 4.1 Изучается зависимость себестоимости единицы изделия (у, тыс. руб.) от величины выпуска продукции (х, тыс. шт.) по группам предприятий за отчетный период. Экономист обследовал n = 5 предприятий и получил следующие результаты (1-й и 2-й столбцы). Полагая, что между переменными х, у имеет место линейная зависимость, определим выборочное уравнение линейной регрессии. Заполним таблицу

Номер	х	у	х2	х*у
1	2	1.9	4	3.8
2	3	1.7	9	5.1
3	4	1.8	16	7.2
4	5	1.6	25	8.0
5	6	1.4	36	8.4
n = 5
Сред нее

Уравнение линейной регрессии имеет вид:

Найдем остатки и коэффициент детерминации.

Решение: Заполним таблицу

Но мер	х	y	y2	=2.12- -0.11x
1	2	1,9	3,61	1,90	0,00	0,22	0,22	0,0484	0.0484	0
2	3	1,7	2,89	1,79	-0,09	0,02	0,11	0,0004	0.0121	0.0081
3	4	1,8	3,24	1,68	0,12	0,12	0	0,0144	0	0.0144
4	5	1,6	2,56	1,57	0,03	-0,08	-0,11	0,0064	0.0121	0.0009
5	6	1,4	1,96	1,46	-0,06	-0,28	-0,22	0,0784	0.0484	0.0036
Сумма	20	8,4	14,26		0	0	0	0,148	0.121	0.027
Сред ние								0,0296=var(y)	0.0242= var( )	0.0054=var( )

var(y)= ; var( )= ; var( )=

Проверим: Var(y)=var( )+var( ); 0.0296=0.0242+0.0054

0.0296=0.0296, отсюда R²=

Т.е. 81,7 % общей вариации себестоимости у зависит от выпуска продукции х. Наша модель не объясняет 18,3 % вариации себестоимости. Эта часть вариации объясняется факторами, не включенными в модель.

Пример 4.2. Показать, что ,где - коэффициент корреляции между и .

Решение:

Тогда

Пример 4.3. Показать, что в случае парной регрессии ,

Решение:

В случае парной регрессии коэффициент детерминации есть квадрат коэффициента переменных и .

Пример 4.4 Показать, что в модели регрессии без свободного члена , оценка МНК для есть

Решение:

Выборочная регрессия для данной модели .

Наблюдаемые значения зависимой переменной связаны с расчетными значениями уравнением .

Оценку найдем из минимизации величины

Найдем

Т.к.

Отсюда

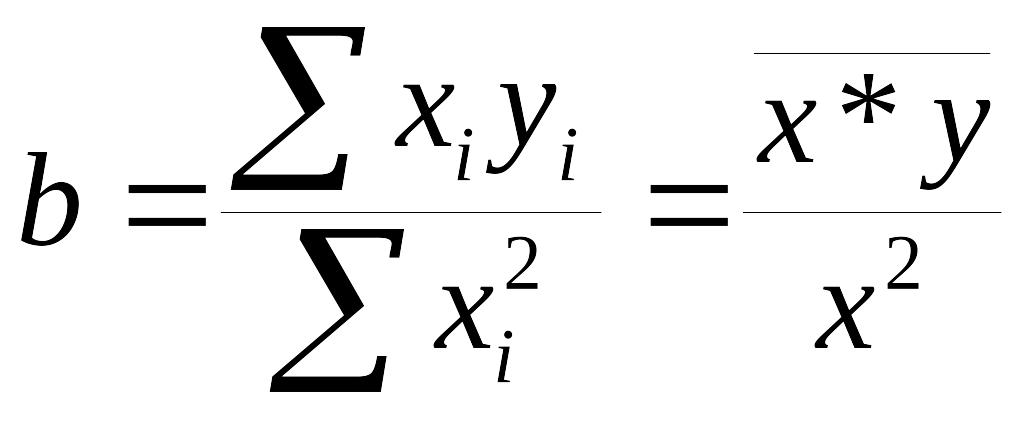
Вычисление при отсутствии свободного члена некорректно.

Пример 4.5. Показать, что в модели регрессии

Оценка для есть

Решение:

Выборочная регрессия для заданной модели есть наблюдаемые значения зависимой переменной связаны с расчетными значениями уравнением

Оценку а найдем из минимизации величины

Найдем

Т.к.

Итак, выборочная регрессия .

Контрольные вопросы:

1.Какой общий вид имеет модель парной линейной регрессии?

2.Перечислите основные причины существования случайного члена в модели парной линейной регрессии.

3.Какой метод используют для проведения регрессионного анализа?

4.В чем суть задачи регрессионного анализа?

5.Какое значение может принимать коэффициент детерминации и почему?

56