5. 2. 1. Расчет четырехпроводной цепи при соединении фаз генератора и приемника «звездой»

Для расчета трехфазной цепи применимы все методы, используемые для расчета линейных цепей. Обычно сопротивления проводов и внутреннее сопротивление генератора меньше сопротивлений приемников, поэтому при расчете таких цепей сопротивления проводов можно не учитывать ( , ). Если полные комплексные сопротивления фаз равны , , , токи в каждой фазе определяются по закону Ома

, , . (5. 4)

Записав уравнение по первому закону Кирхгофа для нейтральной точки N (n), получим

. (5. 5)

5. 2. 1. 1. Симметричная нагрузка приемника

П

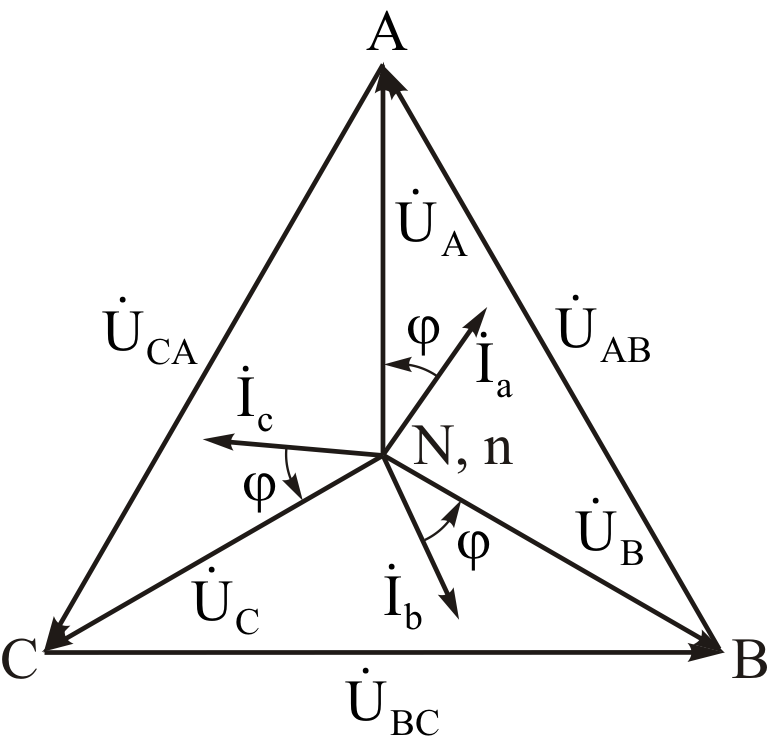
Рис. 5. 8. Векторная диаграмма токов соединения «звезда» при симметричной нагрузке

Рис. 5. 7. Векторно-топографическая диаграмма соединения «звезда» при симметричной нагрузке

ри симметричной нагрузке полные комплексные сопротивления фаз приемника равны между собой

,

где , . В случае симметричной системы ЭДС действующие значения фазных токов равны и углы сдвига фаз между токами и напряжениями одинаковы: (рис. 5. 7).

Из векторной диаграммы токов для симметричного приемника (рис. 5. 8) видно, что сумма векторов фазных токов равна 0 ( ). Соответственно и ток в нулевом проводе . Из этого следует, что при подключении к симметричной системе ЭДС симметричной нагрузки по схеме «звезда» необходимости использования нулевого провода нет.

5. 2. 1. 2. Несимметричная нагрузка приемника

При подключении несимметричной нагрузки ( , ) к симметричной системе ЭДС токи в фазах нагрузки различны и определяются по закону Ома (5. 4). Ток в нейтральном проводе будет равен сумме фазных токов (рис. 5. 9)

.

В случае идеального нулевого провода ( ) падение напряжения на нем равно 0 и фазные напряжения нагрузки равны фазным напряжениям генератора:

, , ,

а значение фазного напряжения (рис. 5. 10). Таким образом, нейтральный провод обеспечивает симметрию фазных напряжений приемника при несимметричной нагрузке.

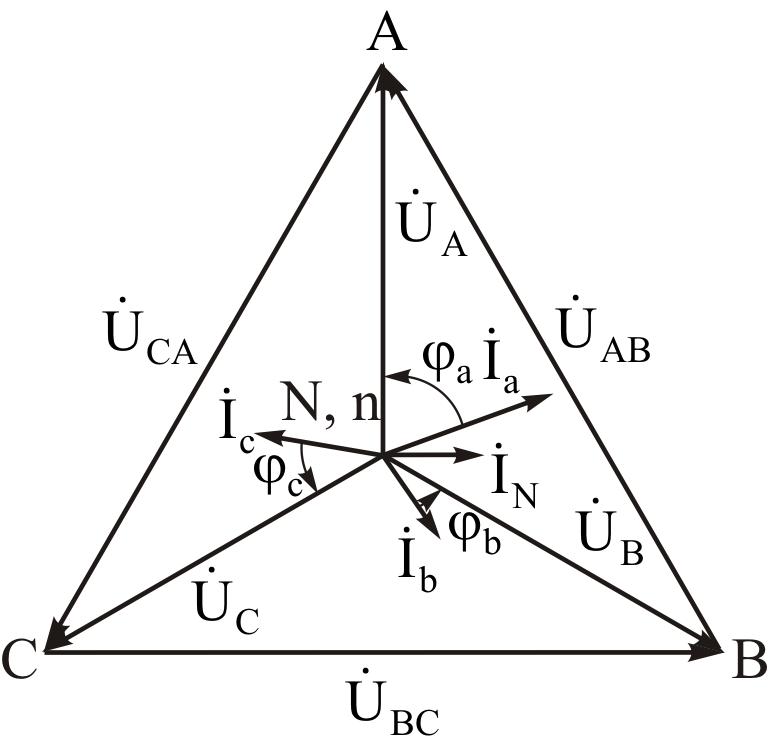
Рис. 5. 9. Векторная диаграмма токов соединения «звезда» при несимметричной нагрузке

Рис. 5. 10. Векторно-топографическая диаграмма соединения «звезда» при несимметричной нагрузке

Учитывая сказанное, в трехфазных электрических цепях однофазные несимметричные нагрузки подключают к симметричной системе ЭДС по четырехпроводной схеме. В этом случае режим работы каждой фазы нагрузки, находящейся под неизменным фазным напряжением генератора, не будет зависеть от режима работы других фаз.

5. 2. 2. Расчет трехпроводной цепи при соединении фаз генератора и приемника «звездой»

Схема трехпроводного соединения «звезда» приведена на рис. 5. 11. При таком соединении точки N и n не связаны между собой проводником и меж

Рис. 5. 11. Схема трехпроводного соединения фаз генератора и приемника «звездой»

ду ними может возникать разность потенциалов , которую называют напряжением смещения нейтрали.

Для трехпроводной цепи сумма фазных токов нагрузки в точке n равна 0 ( ). В случае симметричной нагрузки приемника , , , сумма фазных напряжений приемника , напряжение смещения нейтрали и расчет цепи проводится так же, как в п. 5. 2. 1. 1.

В случае несимметричной нагрузки приемника ( ) напряжение смещения нейтрали . Для его определения используют метод двух узлов (см. п. 2. 3. 6), так как схема соединения «звезда» имеет только 2 узла: n и N. Уравнение для определения будет иметь вид

, (5. 6)

где , , – комплексные проводимости соответствующих фаз нагрузки приемника.

Очевидно, что при напряжения на фазах приемника будут отличаться от напряжений фаз генератора и друг от друга. По второму закону Кирхгофа

, , . (5. 7)

Зная фазные напряжения приемника, определяют фазные токи

, , . (5. 8)

Рис. 5. 12. Векторно-топографическая диаграмма трехпроводного соединения «звезда» при несимметричной нагрузке

Векторно-топографическая диаграмма при подключении несимметричной нагрузки к трехфазной симметричной системе ЭДС по трехпроводной схеме «звезда» показана на рис. 5. 12.

При изменении величины (или характера) фазных сопротивлений напряжение смещений нейтрали может значительно изменяться. При этом нейтральная точка приемника n на диаграмме может занимать разные положения, а фазные напряжения приемника , и могут существенно отличаться друг от друга.

Таким образом, при несимметричной нагрузке и отсутствии нейтрального провода фазные напряжения нагрузки не равны фазным напряжениям генератора, так как на нагрузку воздействуют только линейные напряжения генератора. Несимметричная нагрузка в таких условиях вызывает несимметрию ее фазных напряжений , , и смещение ее нейтральной точки n из центра треугольника напряжений (смещение нейтрали). Из вышеперечисленного следует, что использование нейтрального провода позволяет:

• выравнивать фазные напряжения приемника при несимметричной нагрузке;

• подключать к трехфазной цепи однофазные приемники с номинальным напряжением в раз меньше номинального линейного напряжения сети.

В цепь нейтрального провода нельзя ставить предохранитель, так как перегорание предохранителя приведет к разрыву нейтрального провода и появлению значительных перенапряжений на фазах нагрузки.