1. Фізичні основи роботи перетворювачів інформації

§ 1.1. Класифікація і характеристики перетворювачів інформації

У кожному з елементів розпорядчої ланки локальної системи керування (ЕС, ЕЗ, ЛЕ або ВЕ на рис. В.ЗЗ) здійснюється перетворення інформації за допомогою тих чи інших перетворювачів.

У перетворювачах інформації фізичний сигнал одного виду — вхідний параметр х (рис. 1.1, а)—перетворюється на фізичний сигнал іншого виду— вихідний параметр у, причому вихідний сигнал функціонально пов'язаний із вхідним.

Прикладом перетворювача інформації може бути термоелектро-перетворювач (термопара) (рис. 1.2, а), який перетворює темпера­туру (вхідний сигнал х=t°) на термоелектрорушійну силу (вихід­ний параметр у= ); як відомо, залежить від t°.

За характером роботи перетворювачі бувають розривної дії, або дискретні (наприклад, контакт 4 на рис. В.26, б), та плавної дії (наприклад, реостат 2 на рис. В.26, в).

За структурою перетворювачі поділяються на прості та дифе­ренціальні.

У простому перетворювачі (див. рис. 1.1, а) є один вхідний х і один вихідний у параметр; приклад термоелектроперетворювання наведено на рис. 1.2, а.

Рис. 1.1	Рис. 1.2

Більш складний диференціальний перетворювач: одному вхід­ному параметру х у ньому відповідають два однорідних вихідних параметри та y₂ (див. рис. 1.1,б). Диференціальний перетворю­вач немов складається з двох однотипних простих, з'єднаних між собою таким чином, що будь-яка зміна вхідного параметра спри­чиняє, як правило, однакові за величиною, але різні за знаком прирости вихідних параметрів: якщо один із них збільшується, то інший відповідно зменшується. Прикладом диференціального пе­ретворювача може бути реостат (див. рис. 1.2,б): вхідним пара­метром є лінійне переміщення l рухомого контакта, вихідними — дві напруги та ; якщо повзун переміщується, припустимо, вгору, то напруга при цьому зменшується, а U₂ відповідно збіль­шується.

За видом вихідної величини перетворювачі інформації поділяються на: 1) перетворювачі з механічним переміщенням на виході; 2) на виході яких - тиск газу або рідини; 3) з термічною величиною на виході; 4) з електричною величиною.

Залежно від виду вхідної вели­чини бувають такі перетворювачі: зусилля; механічного переміщення; рівня рідини; швидкості обер­тання; тиску рідини або газу; витрати рідини або газу; темпера­тури; вологості, тощо.

Робота перетворювача описується двома основними характе­ристиками: статичною та динамічною.

Статичною характеристикою перетворювача називається залеж­ність вихідної величини від вхідної , якщо вхідна ве­личина змінюється настільки повільно, що в кожний момент часу її можна вважати незмінною.

Статична характеристика перетворювача плавної дії часто має певний гістерезис: зміни вихідної величини у при збільшенні вхід­ного параметра х не збігаються зі змінами у при зменшенні х. При­близний вигляд висхідної та низхідної віток статичної характеристики (штрихові криві) деякого перетворювача плавної дії по­казано на рис. 1.3. Великий гістерезис у перетворювачах інформації неприпустимий. Невеликим гістерезисом можна знехтувати, вва­жаючи статичною характеристикою певну усереднену криву (рис. 1.4). Крутість статичної характеристики називається чутливістю S перетворювача. Для ділянки АВ статичної характеристики чутли­вість

(1.1)

Статична характеристика перетворювача розривної дії має ін­ший вигляд, наприклад, як на рис. 1.5: при певному значенні вхід­ної величини стрибкоподібно збільшується вихідна вели­чина (спрацьовування), а при відбувається зворотний процес (відпускання).

Рис. 1.3	Рис. 1.4	Рис. 1.5

До статичних характеристик перетворювачів інформації став­ляться певні вимоги: однозначність (мінімальний гістерезис); ста­більність у часі; ідентичність для однотипних перетворювачів; для перетворювачів плавної дії — по можливості лінійність при висо­кій чутливості.

Зміна величини y на виході перетворювача залежно від змін вхідної величини x відбувається, як правило, не миттєво, а з деяким запізненням, яке зумовлюється часом перебігу фізичних процесів у самому перетво­рювачі. Ця залежність становить динамічну характеристику перетворювача. Один із способів вираження динамічної характеристики перетворювача плавної дії полягає в тому, що аналізується зміна вихідної величини у у часі після того, як у деякий момент часу вхідна величина х зазнає стрибкоподібної зміни від початкового значення до кінцевого х_к.

Диференціальне рівняння, що описує динамічні властивості пе­ретворювачів інформації, має вигляд

(1.2)

де та означають, що величини у та х змінюються у ча­сі t. Усі члени цього рівняння слід поділити на , і тоді, позна­чивши ; ; , дістанемо

(1.3)

де ( і , — сталі часу; К— коефіцієнт передачі).

Якщо для деякого перетворювача = =0, то вихідна вели­чина змінюється згідно з законом

(1.4)

Такий перетворювач становить просту безінерційну (ідеальну) ланку: при стрибкоподібних змінах х(t) вихідна величина у(t) теж змінюється стрибкоподібно.

Стрибкоподібну зміну х(t) в момент θ від початкового значен­ня до кінцевого х_к показано на рис. 1.6, , статичну характерис­тику деякого перетворювача — на рис. 1.6, б; зміну величини у(t) на виході цього перетворювача, якщо він становить просту ідеаль­ну ланку, — на рис. 1.6, в.

Якщо Т₂= , але , то розв'язок диференціального рівнян­ня за умови стрибкоподібної зміни х(t) від до x_к у момент ча­су θ буде такий:

(1.5)

де початкове значення y(t); — кінцеве значен­ня y(t); e— основа натуральних логарифмів; t — час.

Цей перетворювач є простою аперіодичною ланкою першого порядку (рис. 1.7, а).

Якщо в рівнянні (1.3) жоден коефіцієнт не дорівнює нулю, то такий перетворювач є ланкою другого порядку; проте розв'язок цього рівняння залежить від співвідношення між Т₂ та Т₁.

Рис. 1.6

При

(1.6)

де

Такий перетворювач становить просту аперіодичну ланку дру­гого порядку (рис. 1.7,6).

Якщо ж <2, то

, (1.7)

де — кутова частота коливань, Т' — стала часу обвідної експоненти,

Цей перетворювач — проста коливальна ланка другого порядку із затухаючим перехідним процесом (рис. 1.7, в).

Рис. 1.7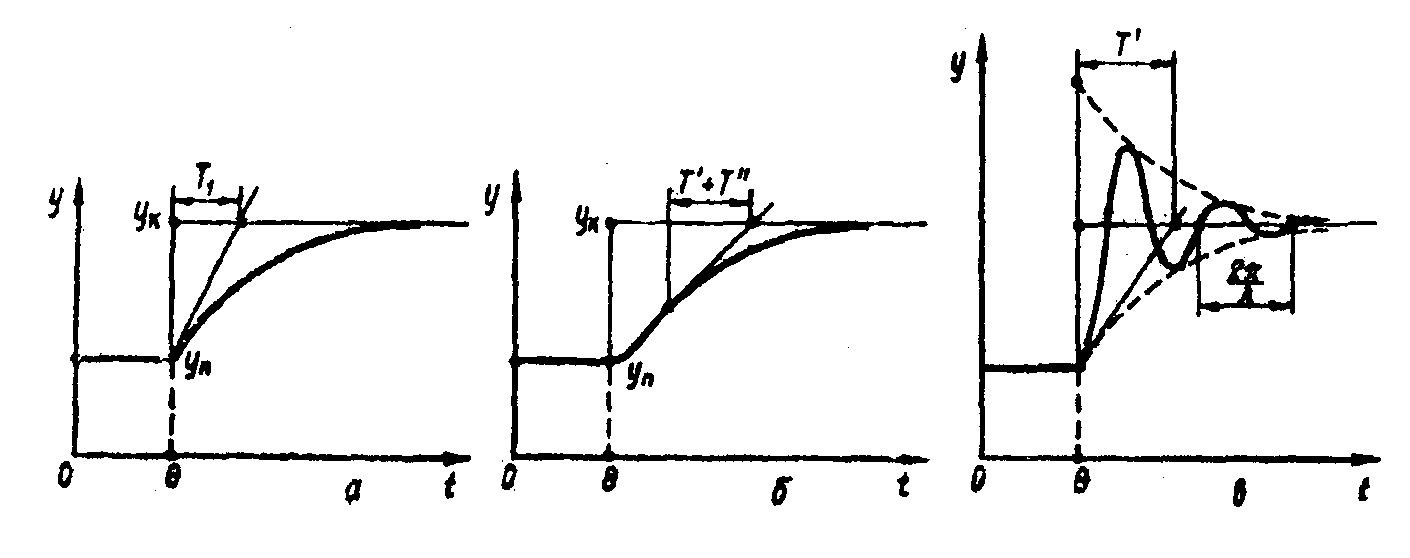

Основна вимога до динамічних характеристик перетворювачів — досягнення якомога меншої тривалості перехідного процесу.