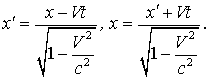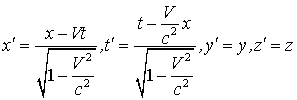1.3. Преобразования Лоренца
Физический процесс - это последовательность событий. Событие определяется местом (координатами), где оно произошло, и моментом времени, когда оно произошло.
Пусть
координаты некоторого события в системе
отсчета I равны
,
а в системе II они
.
Установим связь между ними, исходя из
принципов Эйнштейна.
Искомая связь должна быть линейной т.к. закон инерции подтверждается при всех скоростях, вплоть до максимальной скорости с (движение по прямой линии в системе I остается таковым и в системе П). Поэтому форма связи должна быть следующей:
|
(1.1) |
Здесь
учтено, что
и
в
одном случае обращаются в нуль вместе
(нулю равны координаты точки О' системах
II и I соответственно); то же относится к
х
и
(точка
О). Множитель
в
обеих формулах один и тот же, т.к. системы
I и II совершенно равноправны. Координаты
y
и
z
не меняются, т.к. в направлении осей y
и
z
движение систем отсутствует.
Формулы (1.1) относятся к любым событиям, но множитель можно определить, разумеется, рассматривая какое-либо частное событие. Для определения , рассмотрим распространение света в направлении оси абсцисс от начала координат - приход света в точку х1 в момент t1 (в системе I), что также означает приход его в точку х1' в момент t1' (в системе П).
В соответствии со вторым принципом Эйнштейна, путь света в системе I и II равен
|
(1.2) |
Еще два равенства должны выполняться на основе формул перехода (1.1)
|
(1.3) |
Если
последние два равенства перемножить и
заменить
на
основании (1.2)
через
,
то, после сокращения на
,
получим
откуда
|
(1.4) |
Подставляя найденное значение ( в формулы (1.1), получим
|
(1.5) |
Из
второй формулы легко определить
(после
замены
на
основании первой формулы) и тогда
окончательно имеем
|
(1.6) |
Такова связь между координатами (включая время) одного и того же события в двух инерциальных системах отсчета I и II (штрихованная система 1 движется относительной не штрихованной I со скоростью V в направлении оси х). Формулы (1.6) известны в науке как преобразования Лоренца. Вся физическая теория (механика, электродинамика и др.) подлежала после их открытия перестройке - такой, чтобы связи (1.6) были учтены. Это было осуществлено в специальной теории относительности (сначала в электродинамике Эйнштейном; позже - в механике).
Из
формул (1.6)
в частности следует: одновременные, но
происходящие в разных точках пространства,
события в системе I не являются таковыми
в системе II. Действительно, если
,
то для одного и того же t имеем
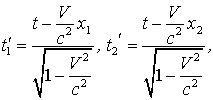
то
есть
.
И
еще, в момент совмещения осей систем I
и II только базовые часы имеют одинаковые
показания, а именно
;
в любой другой точке, отличной от начал
координат, показания находящихся там
часов неодинаковы. Действительно, если
,
но
,
то
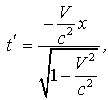
в
системе I
,
а в системе II
.
Если разрешить равенства (1.6) относительно не штрихованных координат (это означает переход II >I), то получим
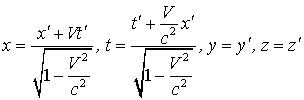
Эти формулы отличаются от (1.6) только тем, что штрихованные и не штрихованные координаты поменялись местами, а скорость (+V) заменена на (- V), что вполне понятно - системы I и II равноправны и I движется относительно II со скоростью (- V).
Если
,
то формулы (1.6)
преобразований Лоренца вырождаются и
принимают вид
Это известные в ньютоновой механике преобразования Галилея. С ними связано представление об абсолютном времени, одинаково текущем во всех системах отсчета (одновременность событий абсолютна - относится ко всем системам отсчета).
Преобразования Лоренца знаменуют в науке новый этап в познании метрических свойств пространства и времени, более глубоких, чем те, которые сложились постепенно в грубом человеческом опыте и отражены в ньютоновой механике. Неудивительно поэтому, что из преобразований Лоренца вытекают кинематические следствия, которые не согласуются со "здравым смыслом". Рассмотрим два основных из них.