
- •Дослідження перехідних характеристик динамічних елементарних ланок Теоретичні відомості до лабораторної роботи № 6
- •1. Елементарна ланка
- •2. Елементарні динамічні ланки
- •2.1. Підсилювальна ланка
- •2.2. Інтегруюча ланка
- •Диференціююча ланка
- •Інерційна ланка
- •Ланка другого порядку
- •Ланка з постійним запізненням
- •3. З'єднання ланок. Передаточні функції з'єднань
Ланка з постійним запізненням
Ця ланка характеризується тим, що відтворює на виході вхідний сигнал без зміни, але з запізненням на час .
Запізнення властиве багатьом елементам автоматики, зокрема, поточно-транспортним пристроям, довгим трубопроводам і іншим елементам. Якщо за вхідну величину прийняти подачу матеріалу на транспортер, а за вихідну - його появу у кінці транспортера, то час запізнення
![]() ,
/19/
,
/19/
де l - довжина транспортера; ν - швидкість його руху.
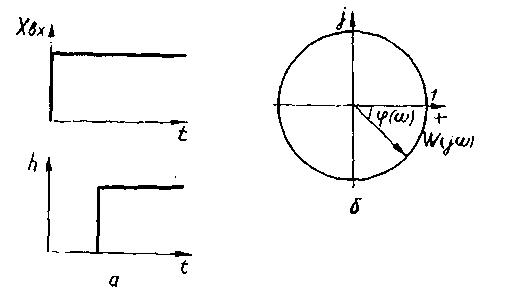
Рис.8. Перехідна характеристика ланки зі сталим запізненням.
Рівняння ланки з постійним запізненням
![]() ,
/20/
,
/20/
при цьому хвих=0
для
![]() .
Вираз /3.35/ показує, що вихідна величина
повторює вхідну зі зсувом у часі на t.
.
Вираз /3.35/ показує, що вихідна величина
повторює вхідну зі зсувом у часі на t.
Ступінчастий вхідний сигнал і перехідна характеристика h(t) =1(t—τ) показані на рис. 8.
Передаточна функція ланки
![]() .
/21/
.
/21/
3. З'єднання ланок. Передаточні функції з'єднань
Складні елементи і системи регулювання завжди можна представити у виді певного з'єднання елементарних ланок. З'єднання ланок бувають трьох видів: послідовне, паралельне і з'єднання зі зворотним зв'язком.
При послідовному з'єднанні ланок вихідна величина однієї ланки є вхідною величиною наступної (рис. 9, а). Оскільки у відповідності з визначенням передаточних функцій
![]()
то
![]() .
/22/
.
/22/
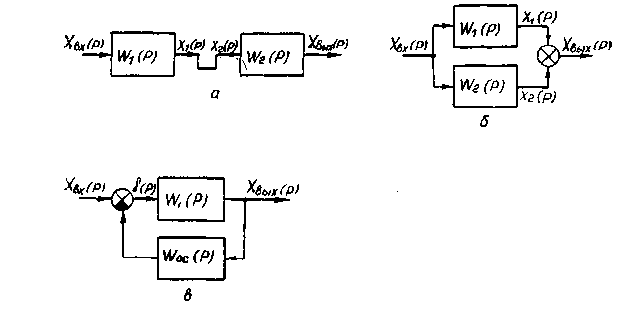
Рис. 9. Типові з'єднання ланок: а - послідовне; б - паралельне; в - з'єднання зі зворотним зв'язком.
З рівності /22/ знаходять передаточну функцію послідовного з'єднання двох ланок:
![]() .
/23/
.
/23/
Отже, передаточна функція послідовного з'єднання двох ланок дорівнює добуткові передаточних функцій цих ланок. Даний результат узагальнюється на будь-яке число послідовно з'єднаних ланок.
При паралельному
з'єднанні (рис. 9,б) на входи всіх ланок
подається та сама вхідна величина хвх,
а їхні вихідні величини сумуються (![]() ).
Тому що
).
Тому що
![]() і
і
![]() ,
то
,
то
![]() .
.
Звідси передаточна функція паралельного з'єднання дорівнює сумі передаточних функцій даних ланок.
![]() .
/24/
.
/24/
Цей результат також узагальнюється на будь-яке число паралельно з'єднаних ланок.
З'єднання зі зворотним зв'язком, назване також зустрічно-паралельним з'єднанням, утворює замкнутий контур передачі сигналів керування (рис. 9, в). Передаточна функція W1(p) називається передаточною функцією прямого ланцюга передачі сигналів, a Wзз (p) - передаточною функцією зворотного зв'язку.
Якщо вихідний сигнал ланки зворотного зв'язку хзз співпадає за знаком з вхідним сигналом хвх, то зворотний зв'язок називається додатнім, а якщо протилежний за знаком - то від’ємним. Додатний зворотний зв'язок підсилює дію вхідного сигналу, а від’ємний - послаблює.
При від’ємному зворотному зв'язку
![]() ;
/25/
;
/25/
![]() ;
/26/
;
/26/
![]() .
/27/
.
/27/
Розв’язавши систему рівнянь /25/ — /27/, знаходять
![]() .
/28/
.
/28/
Отже, передаточна функція з'єднання з від’ємним зворотним зв'язком має вигляд
![]() .
/29/
.
/29/
Якщо зворотний зв'язок додатний, то в знаменнику виразу /29/ необхідно знак «плюс» поміняти на знак «мінус».
Вирази для передаточних функцій різних видів з'єднань ланок застосовують для знаходження передаточних функцій складних систем регулювання.
