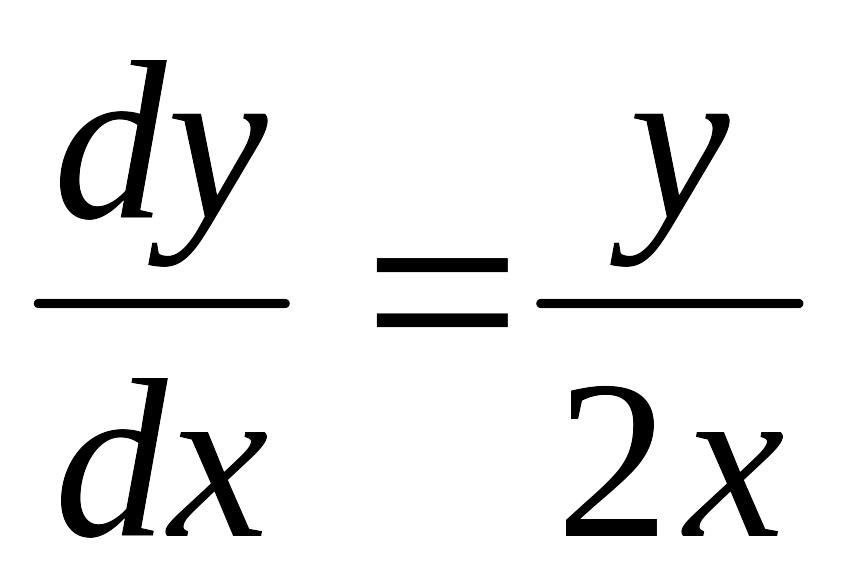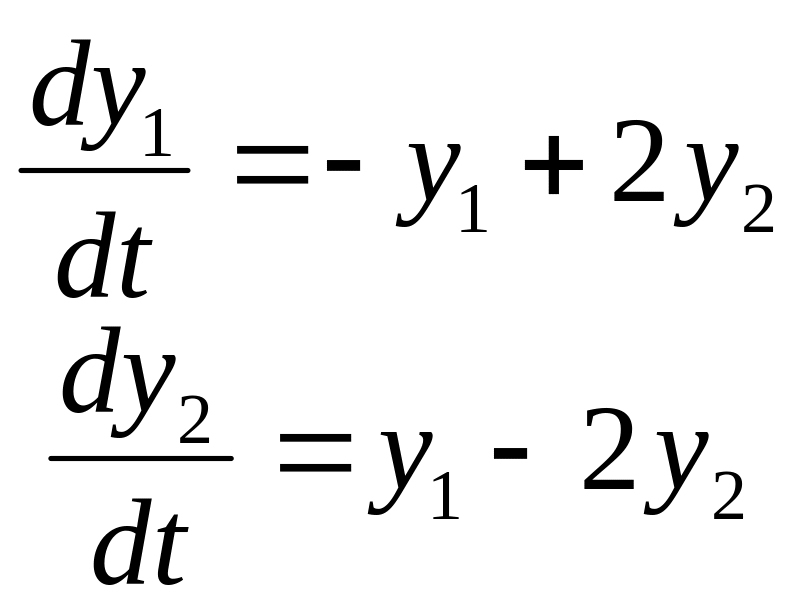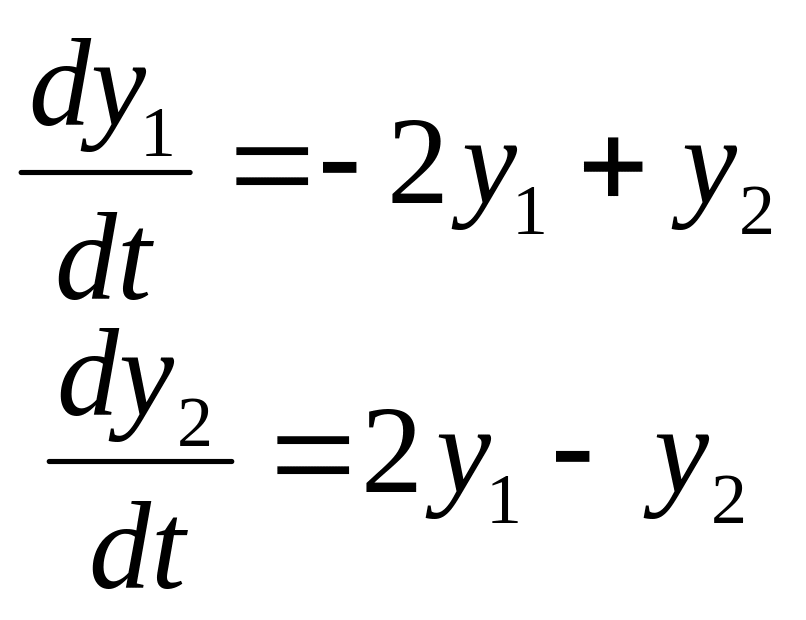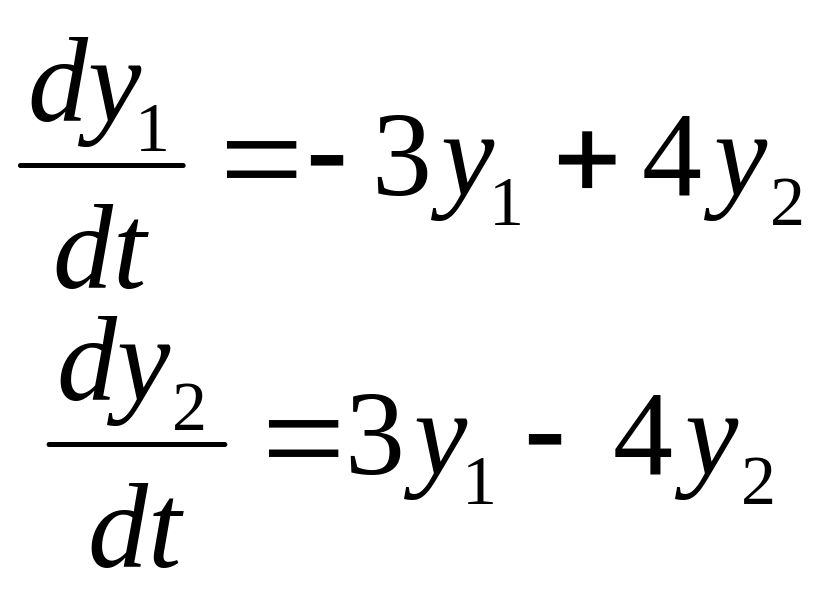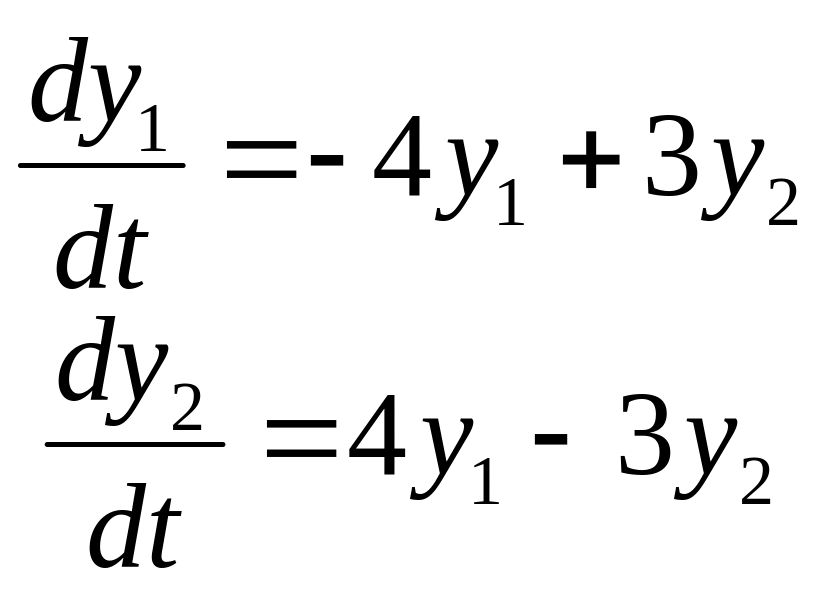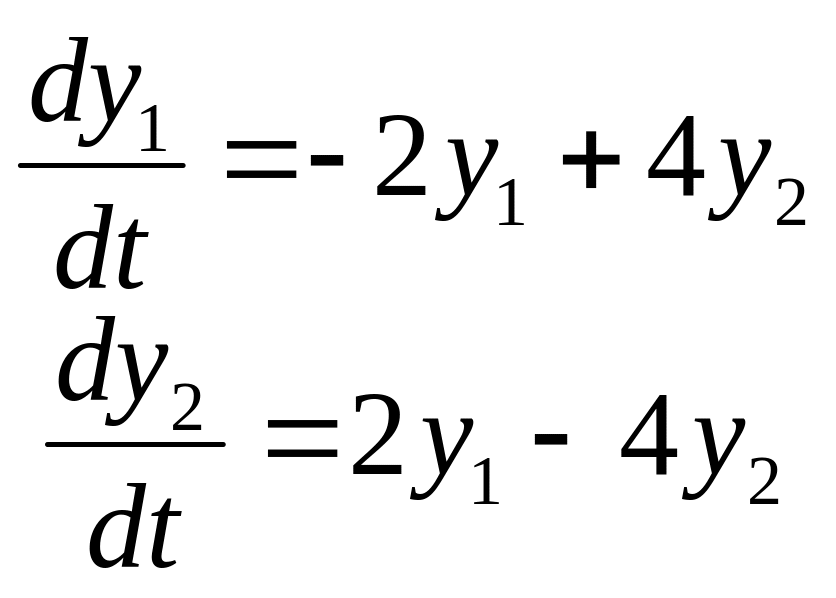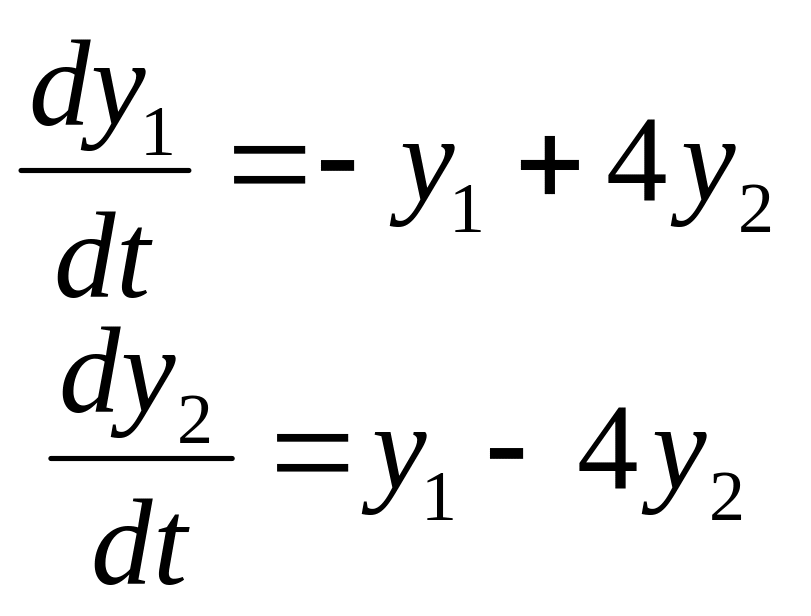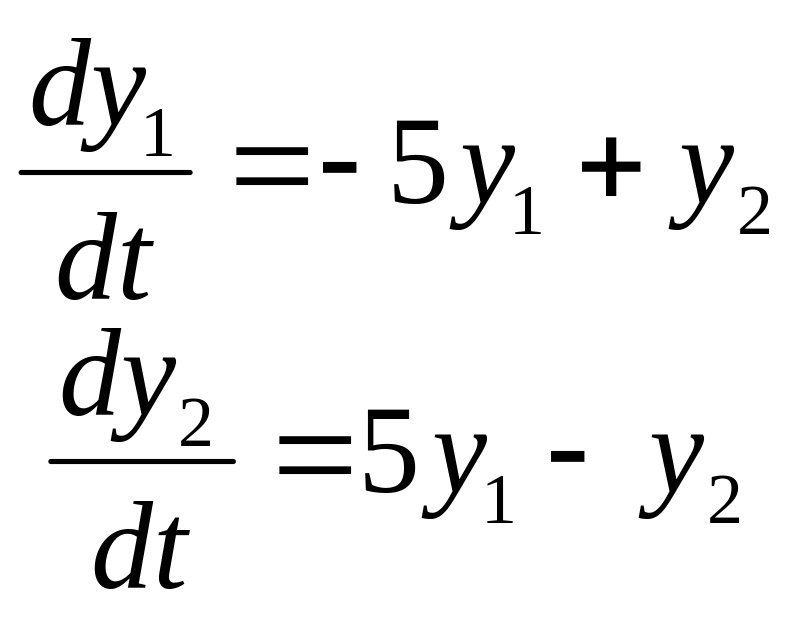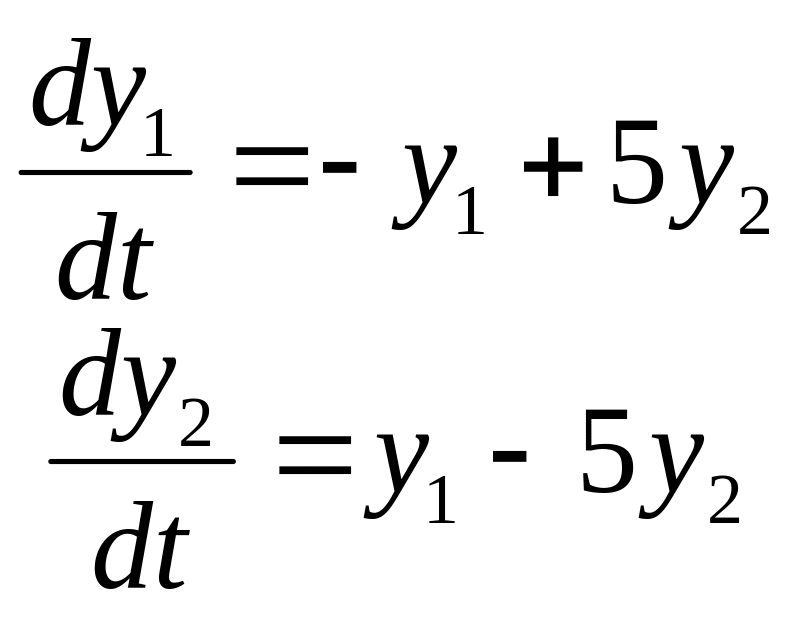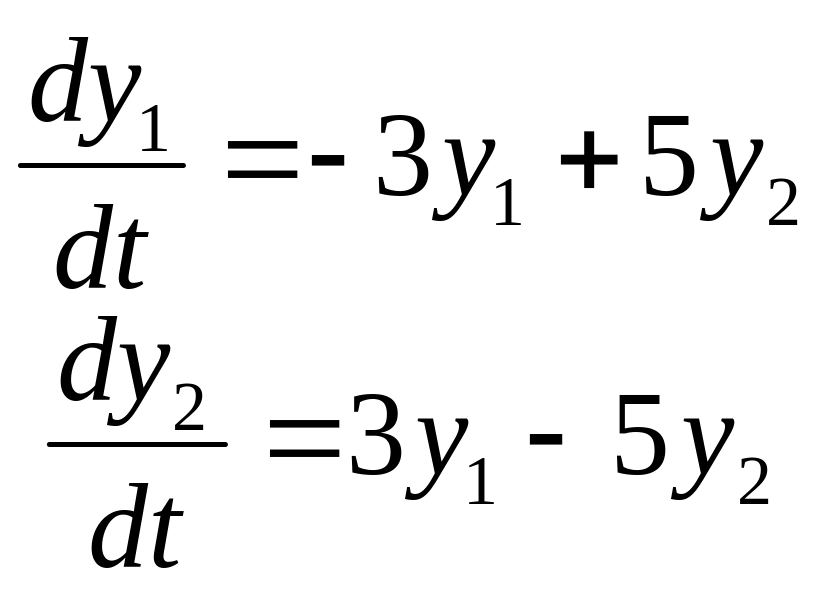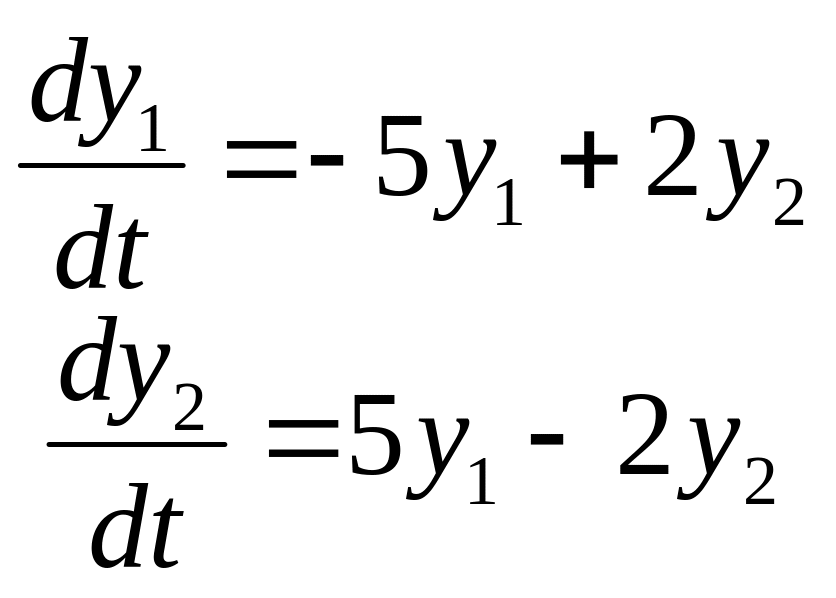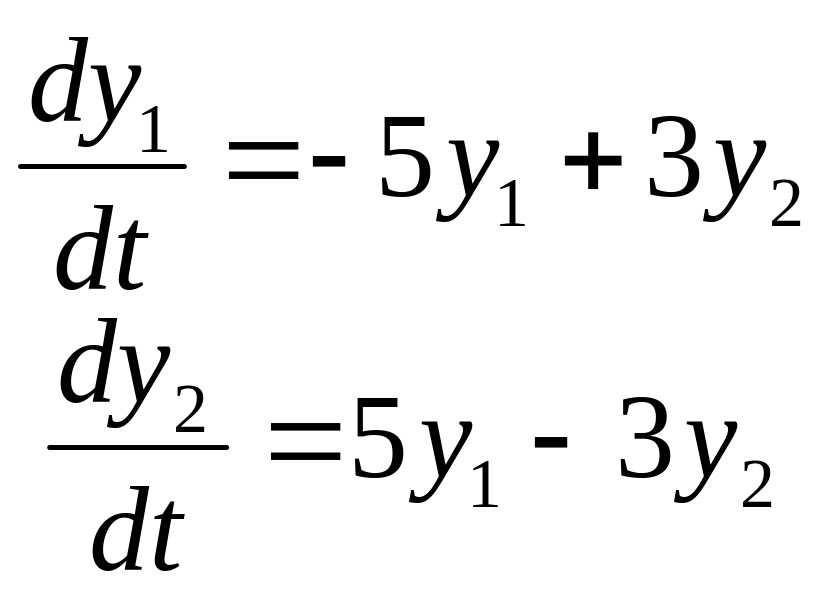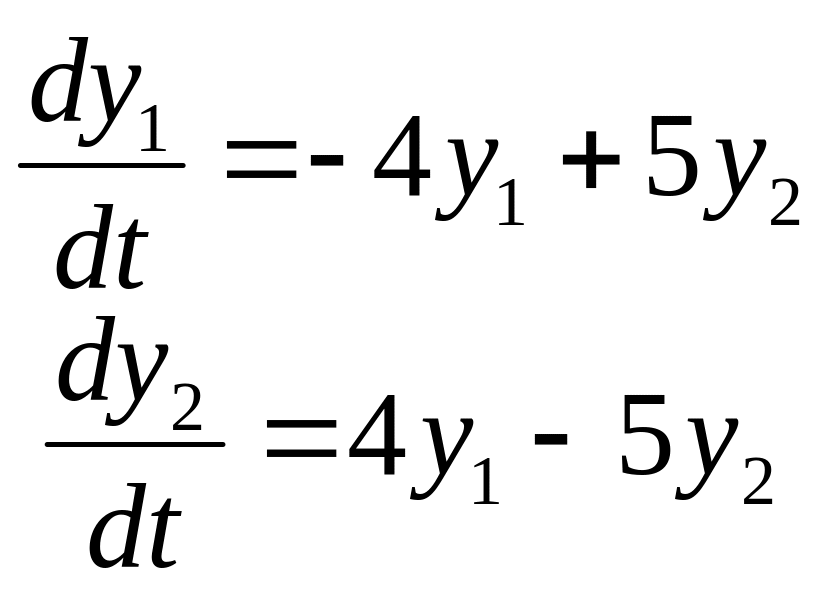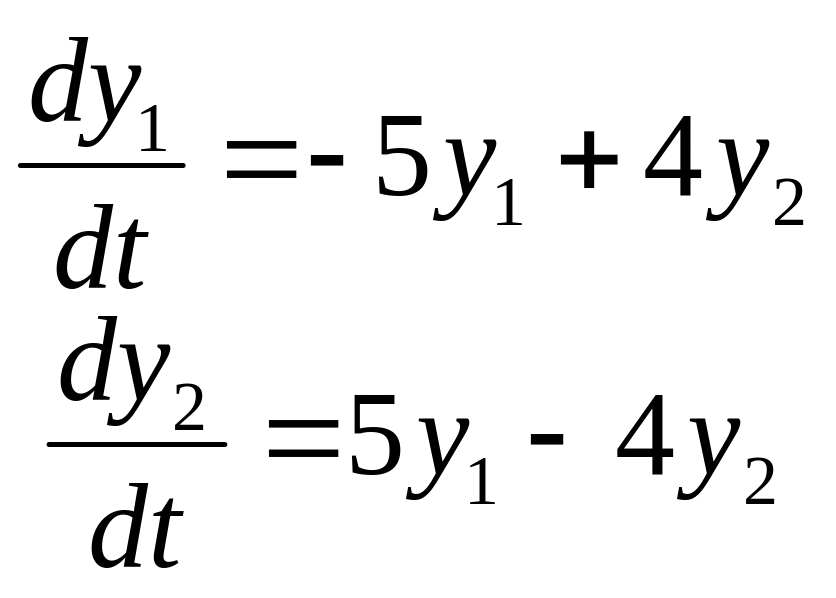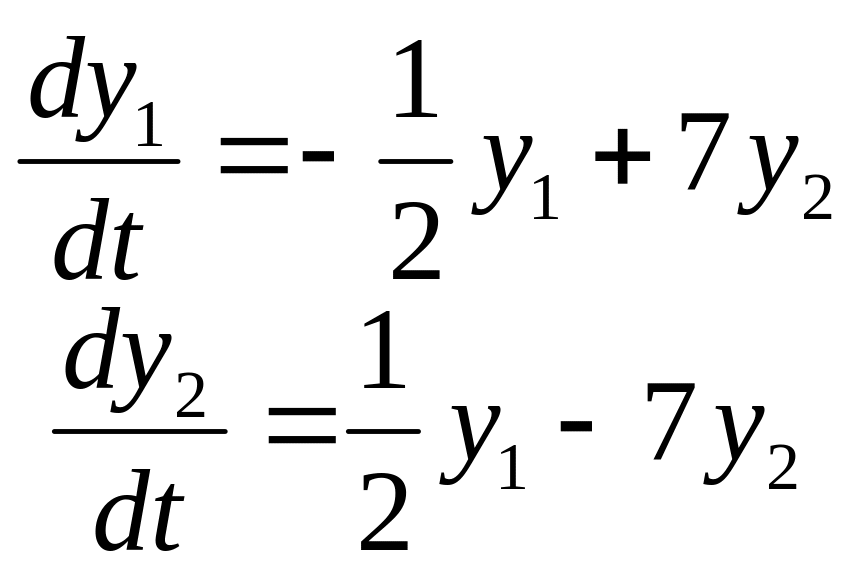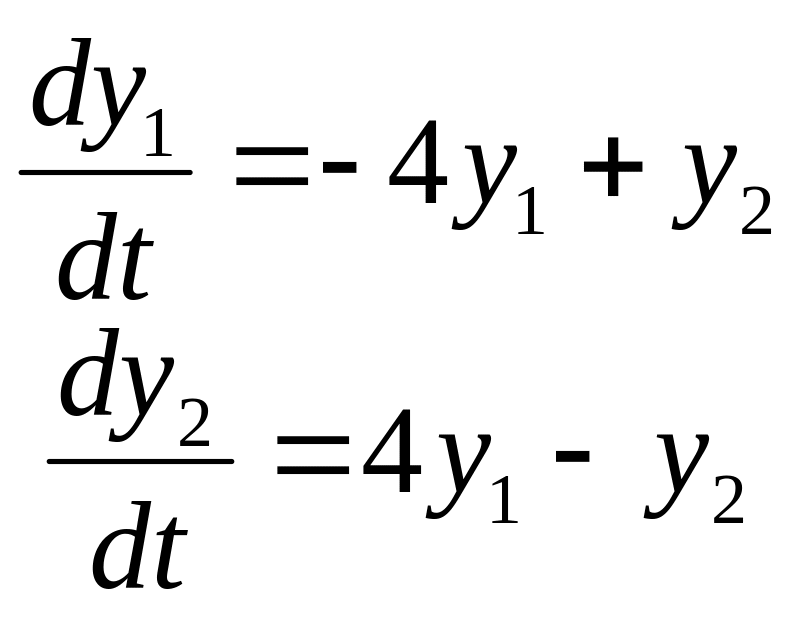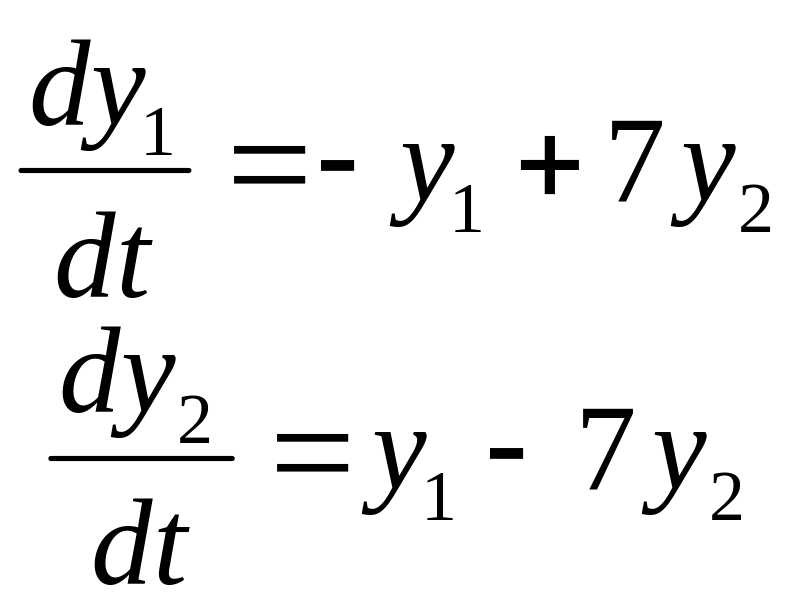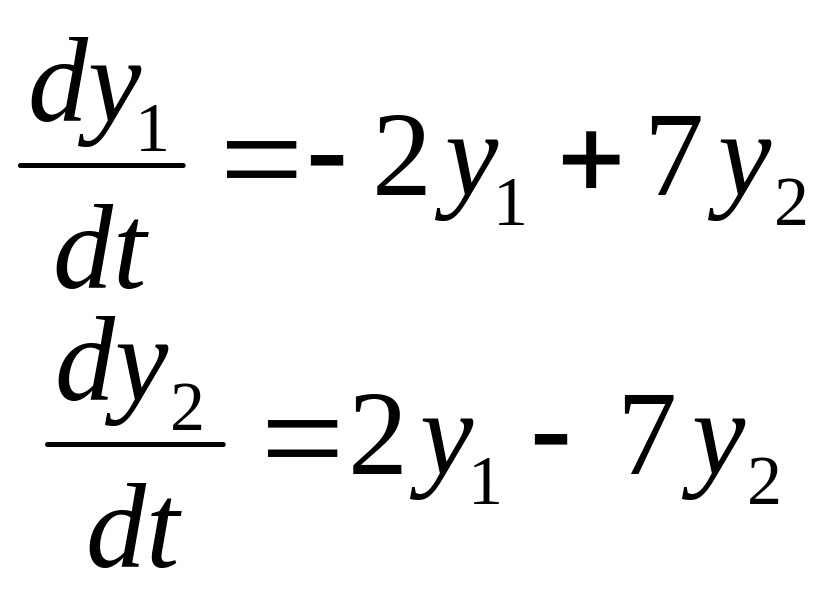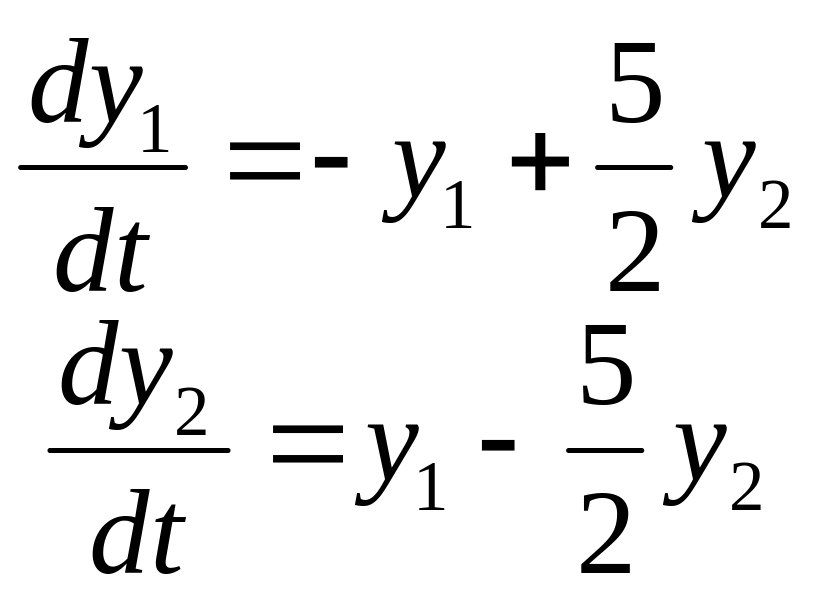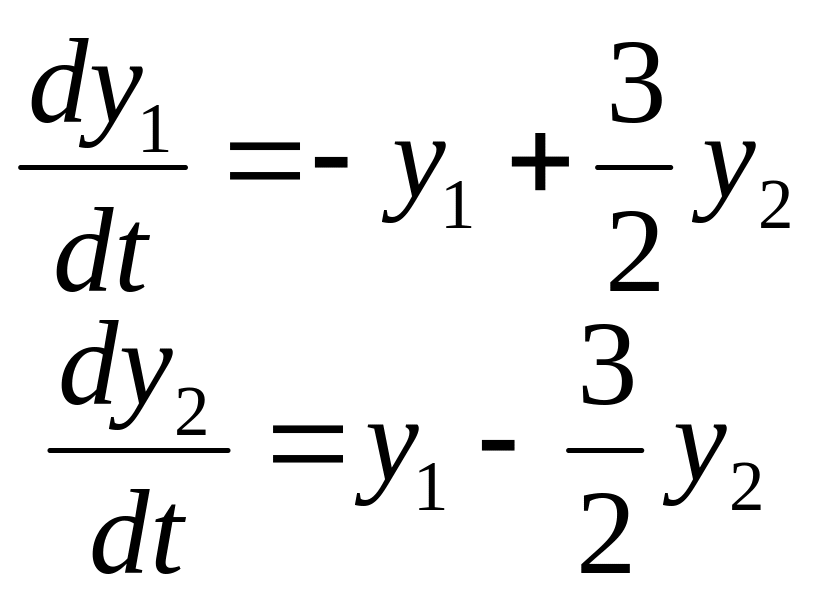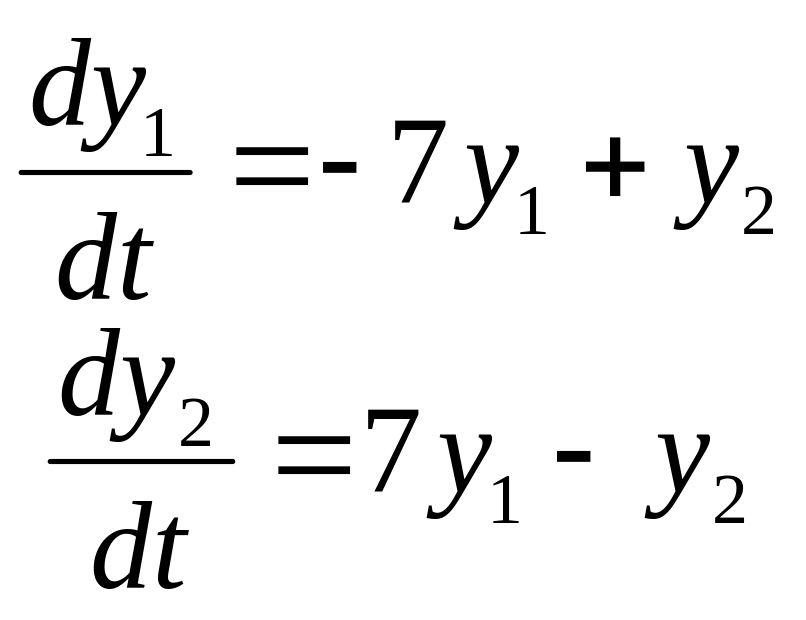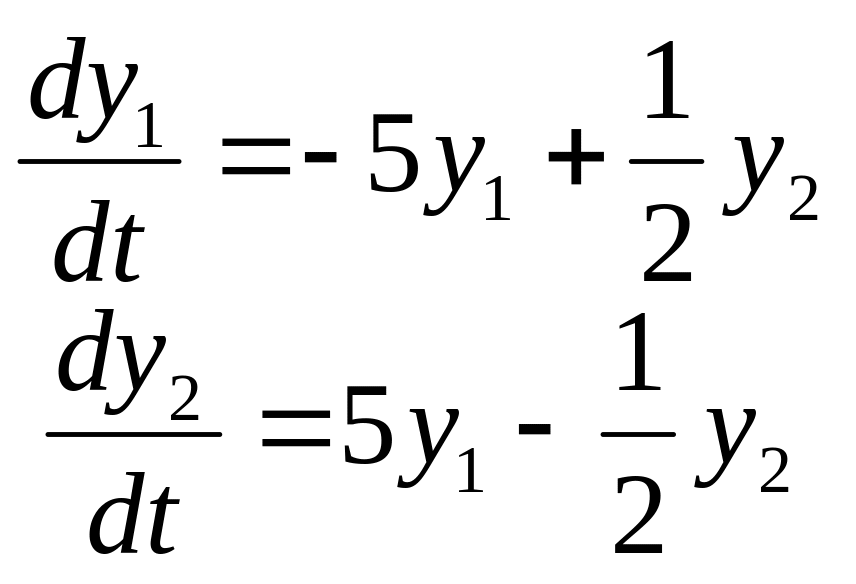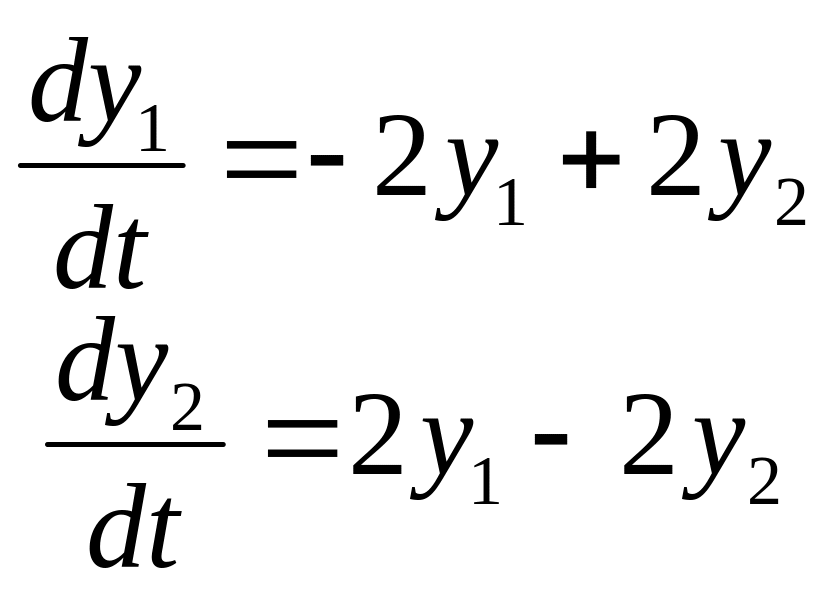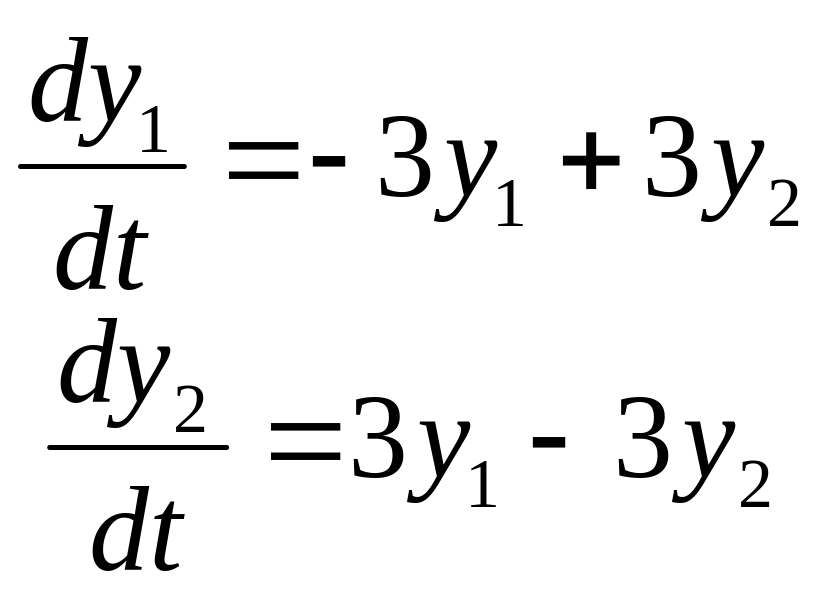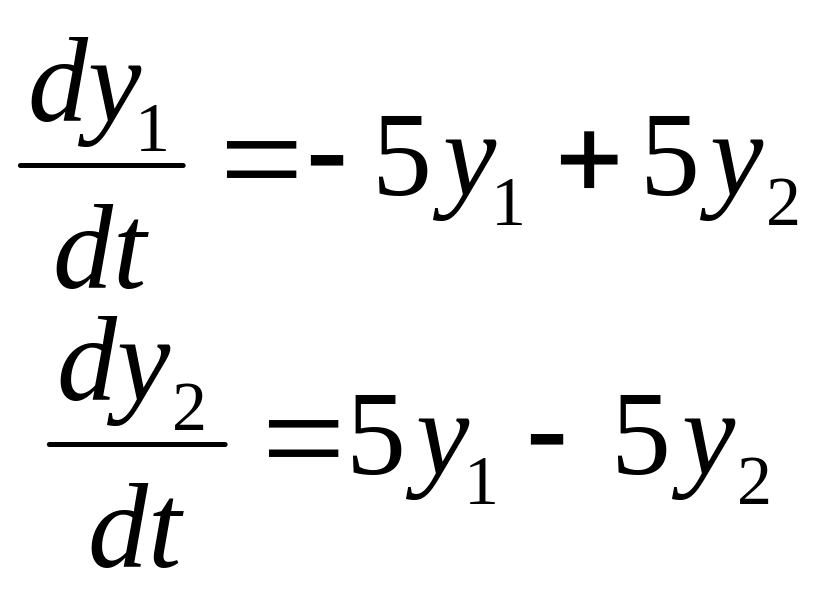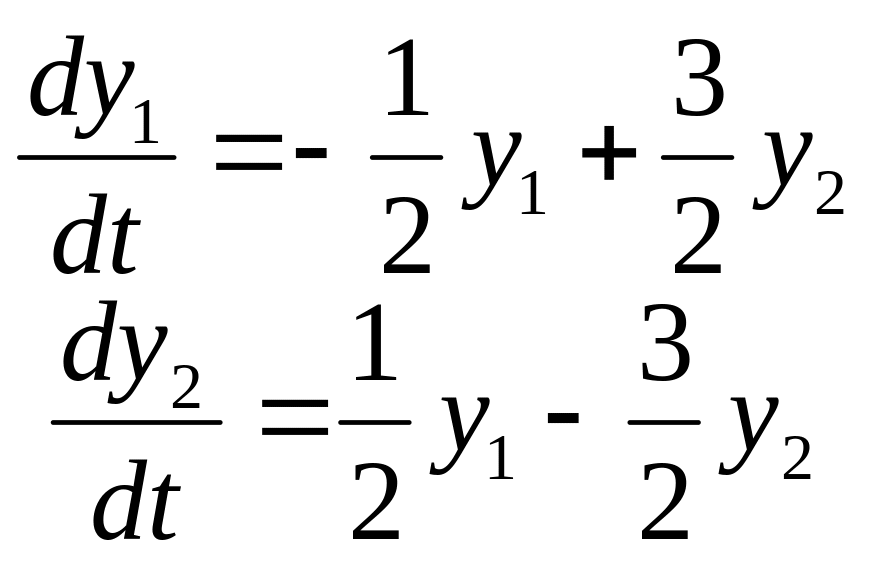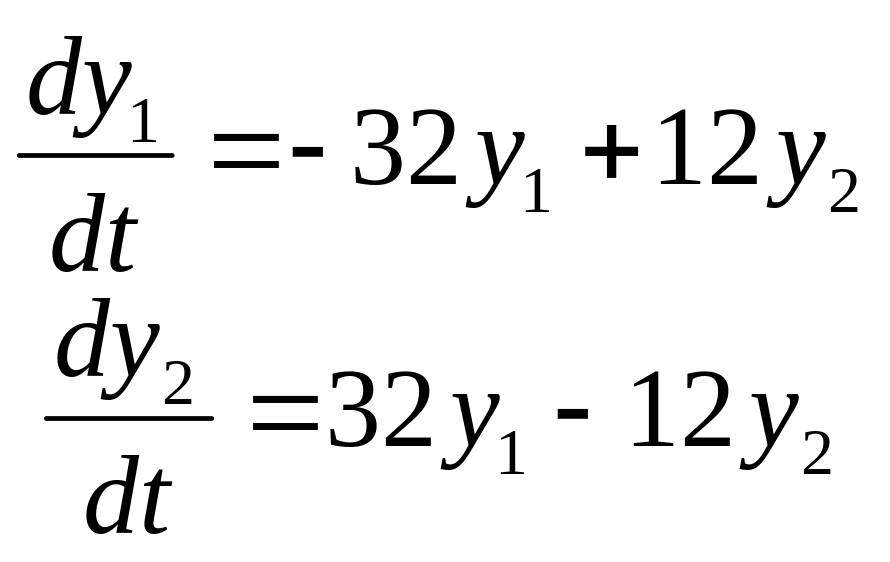- •Тема. Дифференциальные уравнения
- •Типы дифференциальных уравнений первого порядка
- •Уравнения с разделенными переменными
- •Уравнения с разделяющимися переменными
- •3. Однородные уравнения первого порядка
- •Дифференциальные уравнения второго порядка.
- •Типы дифференциальных уравнений второго порядка
- •Линейные однородные уравнение второго порядка с постоянными коэффициентами.
- •2.Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
- •Решение типовых примеров
Решение типовых примеров
1. Найти общее решение (общий интеграл) дифференциального уравнения.
![]()
Данное уравнение не является уравнением с разделяющимися переменными вида y' = f1(x)f2(y). Проверим, не является ли оно однородным дифференциальным уравнением первого порядка вида y' = f(x,y), где
f(lx,ly) = f(x,y):
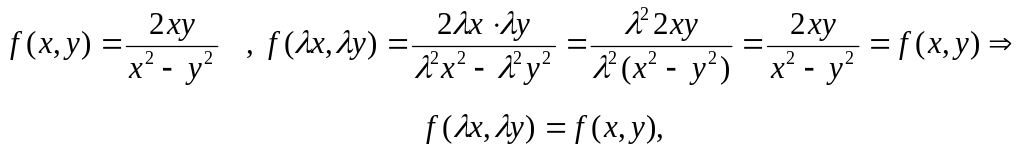
то есть исходное уравнение является однородным.
Введем замену:
![]() .
.
Подставим
в исходное уравнение:
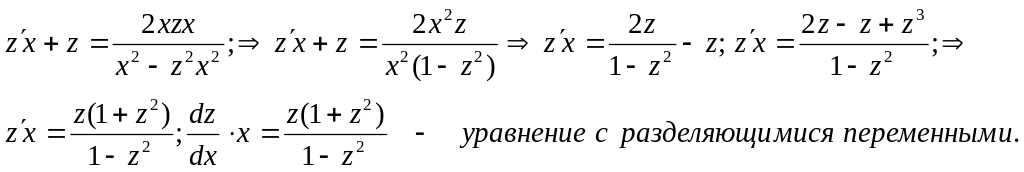
Разделим переменные:
![]()
Проинтегрируем полученное уравнение с разделенными переменными:
![]()
Найдем интеграл левой части уравнения:
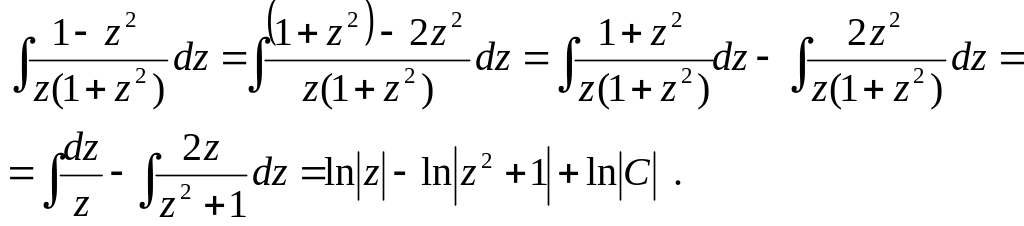 Найдем
интеграл правой части уравнения:
Найдем
интеграл правой части уравнения:
![]()
Приравняем найденные результаты:
![]() .
.
Используем свойства логарифмов:
![]()
Преобразуем равенство:
![]() .
.
Подставим
вместо
![]() получим
получим
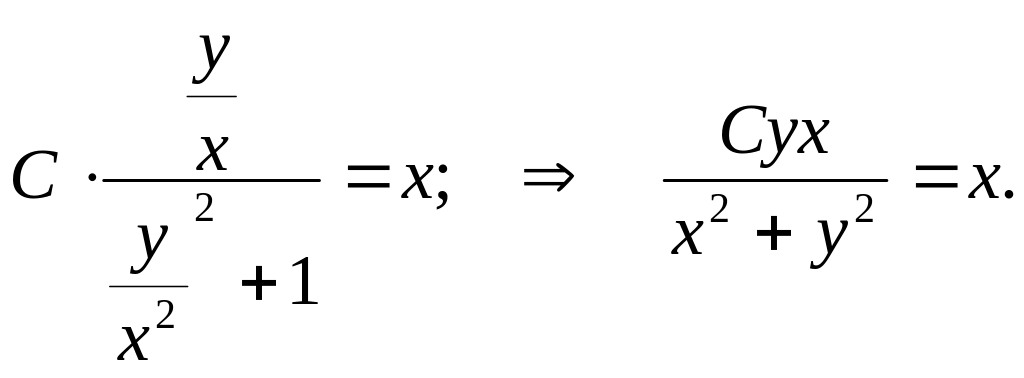
Общее решение данного дифференциального уравнения имеет вид:
![]() ,
,
где С – произвольная постоянная.
2. Найти частное решение однородного дифференциального уравнения второго порядка при заданных начальных условиях:
![]() .
.
Составим для данного д. уравнения характеристическое уравнение:
k2 - 6k + 8 = 0.
Оно имеет два различных, действительных корня
k1 = 2; k2 = 4.
Тогда общее решение уравнения имеет вид:
y = C1e2x + C2e4x,
где С1 и С2 – произвольные постоянные.
Найдем производную общего решения у':
y' = 2C1e2x + 4C2e4x,
Используя начальные условия получим следующую систему уравнений:
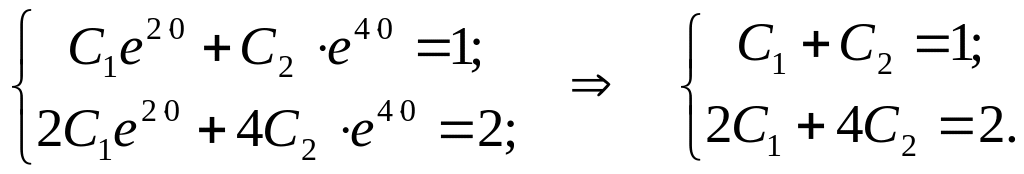
Решаем систему относительно С1 и С2 найдем: С1 = 1; С2 = 0.
Подставим найденные значения С1 и С2 в общее решение, получим искомое частное решение, удовлетворяющее заданным начальным условиям:
y = e2x
3. Найти общее решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами.
![]()
Общее решение данного уравнения находим в виде:
y = y0 + yчаст..
Найдем общее решение у0 соответствующего однородного дифференциального уравнения
![]()
Составим характеристическое уравнение:
k2 – k – 6 = 0.
Найдем его корни: k1 = –2; k2 = 3 - действительные и различные, поэтому общее решение имеет вид:
![]()
где С1 и С2 – произвольные постоянные.
Найдем
частное решение уравнения.![]()
Так как функция f(x) = (2x – 1)e2x имеет вид Pn(x)eax, где Pn(x) = 2x –1 - многочлен 1-ой степени и a = 2 не является корнем характеристического уравнения, то частное решение уравнения (1) запишем в виде:
yчаст.= (Ax +B)e2x,
где А и В – коэффициенты, подлежащие определению. Воспользуемся методом неопределенных коэффициентов.
Найдем yч' и yч"
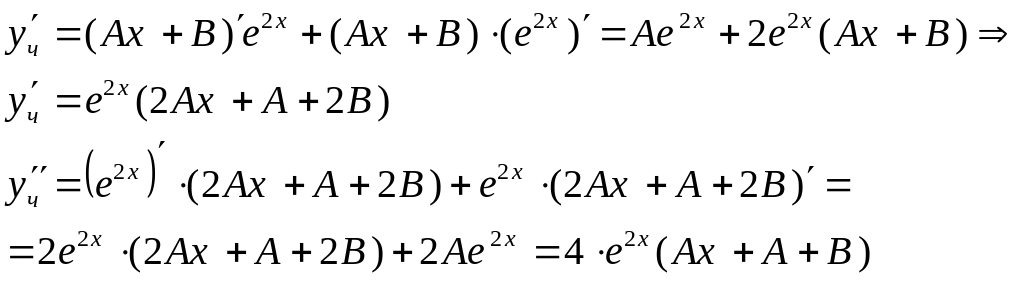
и подставим их в дифференциальное уравнение:
4е2х(Ах +А +В) – е2х(2Ах + А +2В) – 6е2х(Ах + В) =(2х – 1) е2х;
Поделим обе части уравнения на е2х :
4(Ах +А + В) – (2А + А + 2В) – 6(Ах +В) = 2х – 1 Þ
4Ах + 4А + 4В – 2Ах – А – 2В – 6Ах – 6В = 2х – 1 Þ
–4Ах+(3А–4В) = 2х–1 Þ – 4Ax = 2x; 3A– 4B= –1.
Откуда следует, что коэффициенты А и В должны удовлетворять, следующей системе уравнений:
![]()
Решив ее, найдем А= –0,5; B= –0,125.
Подставим найденные значения А и В в уравнение (5) и найдем частное решение:
![]()
Следовательно, общее решение данного линейного неоднородного дифференциального уравнения второго порядка имеет вид:
![]()
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7. |
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17.
|
18.
|
19.
|
20.
|
21.
|
22.
|
23.
|
24.
|
25.
|
26.
|
27.
|
28.
|
29.
|
30.
|
Задание 2. Найти общее решение (общий интеграл) дифференциального уравнения.
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17.
|
18.
|
19.
|
20.
|
21.
|
22.
|
23.
|
24.
|
25. |
26.
|
27.
|
28.
|
29.
|
30.
|
Задание 3. Найти общее решение (общий интеграл) дифференциального уравнения.
1. |
2. |
3. |
4. |
5. |
6. |
7. |
8. |
9. |
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17.
|
18.
|
19.
|
20.
|
21.
|
22.
|
22. |
24.
|
25.
|
26.
|
27.
|
28.
|
29.
|
30.
|
Задание 4. Найти решение задачи Коши и построить соответствующую интегральную кривую.
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12. |
13.
|
14.
|
15.
|
16.
|
17.
|
18.
|
19.
|
20.
|
21.
|
22.
|
23.
|
24.
|
25.
|
26.
|
27.
|
28.
|
29.
|
30.
|
Задание 5. Найти решение задачи Коши и построить соответствующую интегральную кривую.
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17.
|
18.
|
19.
|
20.
|
21.
|
22.
|
23.
|
24.
|
25.
|
26.
|
27.
|
28.
|
29.
|
30.
|
Задание 6. Найти решение задачи Коши и построить соответствующую интегральную кривую.
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17.
|
18.
|
19.
|
20.
|
21.
|
22.
|
23.
|
24.
|
25.
|
26.
|
27.
|
28.
|
29.
|
30.
|
Задание 7. Найти решение задачи Коши и построить соответствующую интегральную кривую.
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17.
|
18.
|
19.
|
20.
|
21. |
22.
|
23.
|
24.
|
25.
|
26.
|
27.
|
28.
|
29.
|
30.
|
Задание 8. Найти решение задачи Коши.
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17.
|
18.
|
19.
|
20.
|
21.
|
22.
|
23.
|
24.
|
25.
|
26.
|
27.
|
28.
|
29.
|
30.
|
Задание 9. Найти общее решение дифференциального уравнения.
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10. |
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17.
|
18.
|
19.
|
20. |
21. |
22.
|
23.
|
24.
|
25.
|
26.
|
27.
|
28.
|
29.
|
30.
|
Задание 10. Найти общее решение дифференциального уравнения.
1.
|
2.
|
3.
|
4. |
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17.
|
18.
|
19.
|
20.
|
21.
|
22.
|
23.
|
24.
|
25.
|
26. |
27.
|
28.
|
29.
|
30.
|
Задание 11. Найти решение задачи Коши.
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17.
|
18.
|
19.
|
20.
|
21.
|
22.
|
23. |
24.
|
25.
|
26.
|
27.
|
28.
|
29.
|
30.
|
Задание 12. Найти общее решение дифференциального уравнения.
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17.
|
18.
|
19.
|
20.
|
21.
|
22.
|
23.
|
24.
|
25.
|
26.
|
27.
|
28.
|
29.
|
30.
|
Задание 13. Найти общее решение дифференциального уравнения.
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17.
|
18.
|
19.
|
20.
|
21.
|
22.
|
23.
|
24.
|
25.
|
26.
|
27.
|
28.
|
29.
|
30.
|
Задание
14. Найти частные
решения
![]() системы дифференциальных уравнений,
которые удовлетворяют условиям
соответственно:
системы дифференциальных уравнений,
которые удовлетворяют условиям
соответственно:
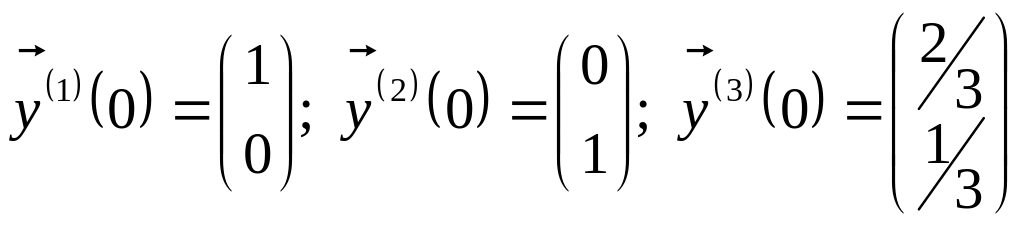 .
Кроме того, в первом случае найти
.
Кроме того, в первом случае найти
![]() и
и
![]() ;
в остальных –
;
в остальных –
![]() .
.
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17.
|
18.
|
19.
|
20.
|
21.
|
22.
|
23.
|
24.
|
25.
|
26.
|
27.
|
28.
|
29.
|
30.
|