Классификация особых точек на плоскости

Рассмотрим конкретный пример:

(1)

Пусть существует особая точка . В нашем случае . Поэтому матрица линеаризации имеет вид

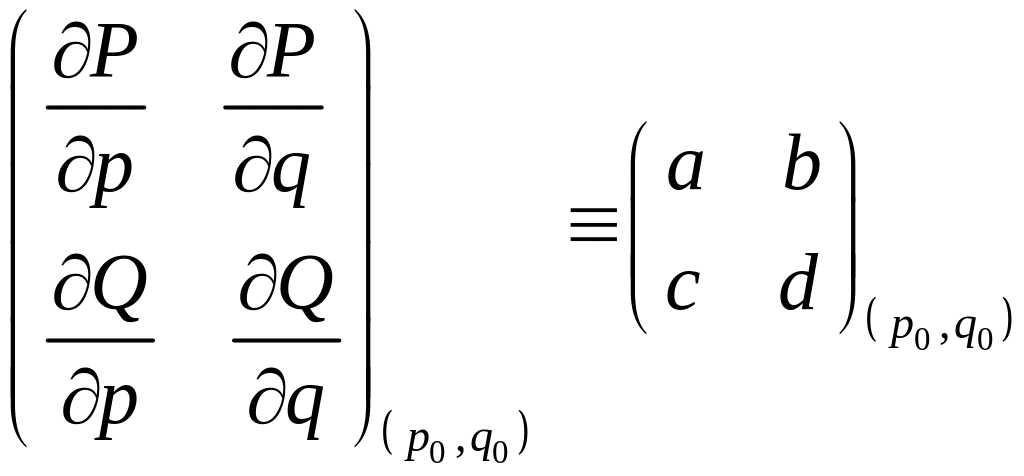. (2)

Из соотношения

(3)

непосредственно имеем

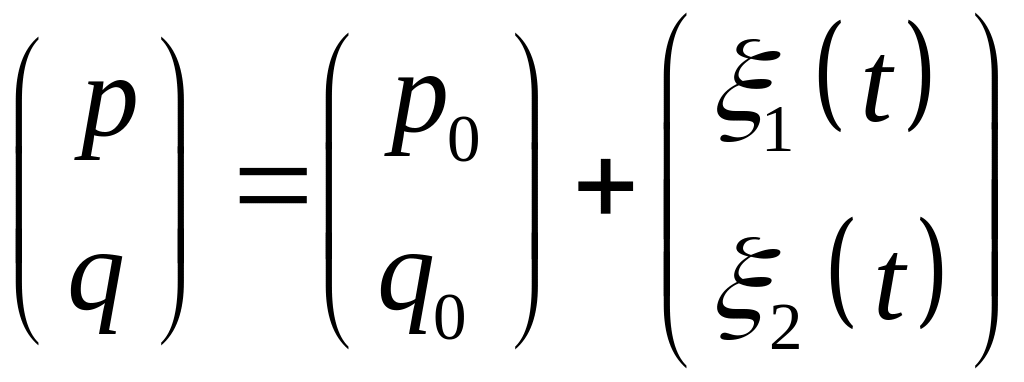. (4)

Далее имеем

. (5)

Характеристическое уравнение имеет вид

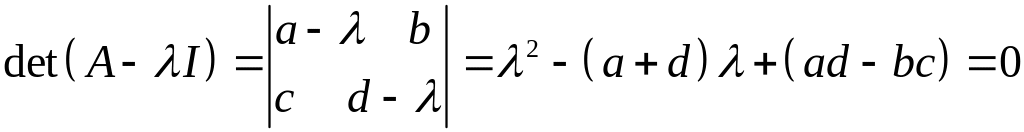
(6)

Матрица Гурвица для уравнения (6) имеет вид

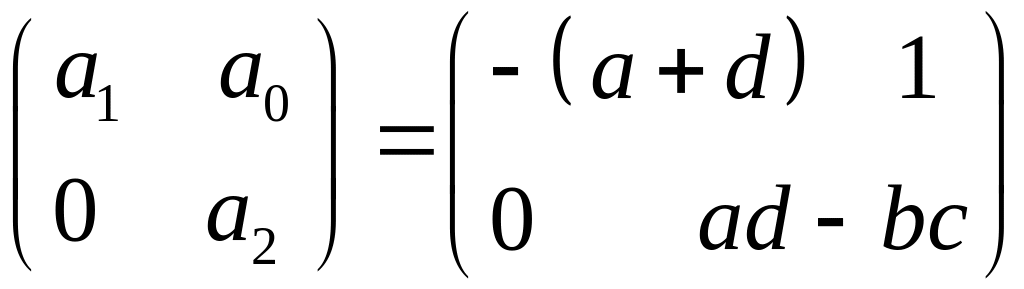. (7)

Для главных диагональных миноров имеем неравенства, определяющие устойчивость

, (8)

. (9)

Далее получаем

. (10)

Итак, необходимые и достаточные условия устойчивости имеют вид

, . (11)

Допустим, что корни характеристического уравнения действительны, различны и отличны от нуля. В этом случае существует линейное преобразование

, (12)

приводящее систему уравнений (5) к диагональному виду

, (13)

Решение этих уравнений тривиально

. (14)

Соотношения (14) можно рассматривать как уравнения фазовых траекторий в параметрической форме (роль параметра играет время ). Исключив из (14) время, получим уравнение фазовых траекторий

. (15)

Если корни и одного знака, то (15) определяет семейство парабол. Особая точка называется в этом случае узлом. Если , то особая точка -узел- является устойчивой. В противном случае особая точка неустойчива.

Если и имеют разные знаки, то уравнение (15) определяет семейство гипербол. В этом случае особая точка называется седлом. Через седло всегда проходят две устойчивые и две неустойчивые траектории.

Случай довольно сложно анализируется ( Л.С. Понтрягин « Обыкновенные дифференциальные уравнения»).

Пусть теперь корни комплексные

. (16)

В этом случае решение системы уравнений (5) имеет вид

, (17)

. (18)

Здесь - вещественные постоянные.

Отсюда имеем

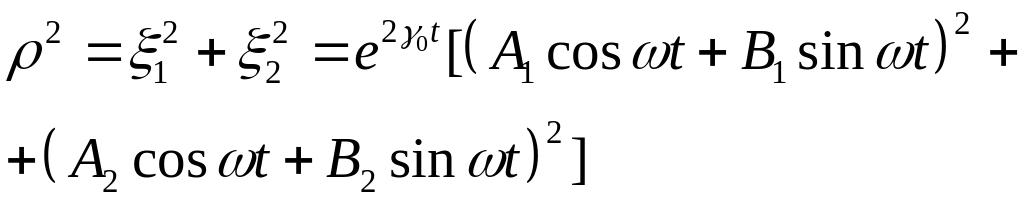. (19)

Если корни чисто мнимые - - то функции являются периодическими с периодом . Это значит, что каждому набору постоянных отвечает замкнутая кривая на фазовой плоскости.

Исключая из формул (17), (18) время, можно показать, что это будет

эллипс. В этом случае особая точка называется центром. Центр называют еще особой точкой эллиптического типа. Центр является устойчивой, но не асимптотически устойчивой точкой покоя.

Если же , то по истечении времени фазовая кривая не замыкается. Получается раскручивающаяся спиралевидная кривая . В этом случае особая точка называется неустойчивым фокусом. Если , то спираль сходится в особую точку – устойчивый фокус. Эта точка является асимтотически устойчивой.

Перечисленные особые точки получены в результате локального анализа и поэтому определяют динамику системы только в окрестности этих точек. Возможны более сложные структуры, возникающие вследствие композиции особых точек.

Фазовый портрет физического маятника – периодически чередующиеся седла и центры.

Решение квадратного уравнения (6) имеет вид

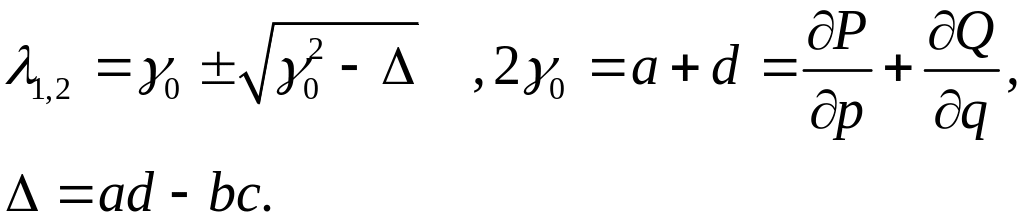(20)

В гамильтоновом случае

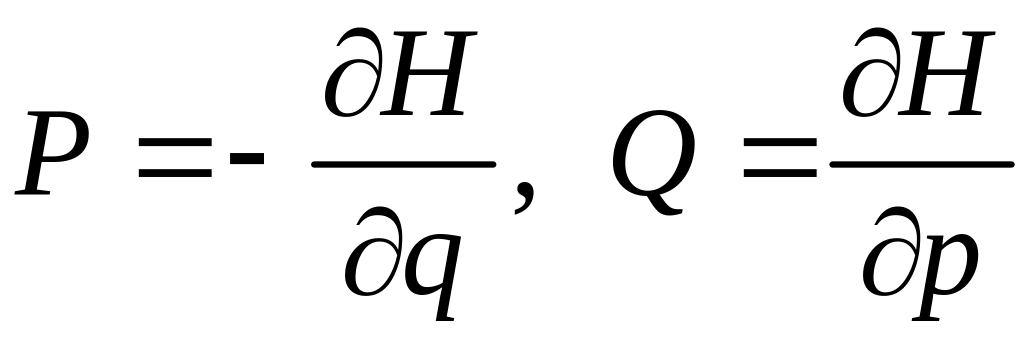, (21)

поэтому

, . (22)

Т.о., в гамильтоновом случае корни характeристического уравнения либо чисто мнимые (комплексно сопряженные) – особая точка –центр, либо вещественные с разными знаками – особая точка- седло, причем гиперболы cедла имеют первую степень.

Генератор Ван-дер-Поля. Автоколебания.

Автоколебания - это незатухающие колебания в нелинейной диссипативной системе, поддерживаемые внешними источниками энергии. Вид автоколебаний и их свойства (амплитуда, частота) определяются самой системой и не зависят от начальных условий (по крайней мере, в определенных пределах).

Автоколебания принципиально отличаются от других колебаний в диссипативных системах тем, что для их поддержания, вообще говоря, не требуется периодических воздействий извне.

В простейших автогенераторах можно выделить:

1) колебательная система с затуханием

2) усилитель

3) нелинейный ограничитель-звено «обратной связи».

Генератор Ван-дер-Поля

Рассмотрим генератор на триоде с колебательным контуром в цепи сетки, индуктивно связанным с анодной цепью.

Случайно возникшие в - контуре малые колебания через катушку в анодной цепи, индуктивно связанную с катушкой колебательного контура, управляют анодным током лампы, который может усиливать колебания в контуре. При условии, что потери в контуре меньше, чем вносимая так энергия, амплитуда колебаний в контуре нарастает. С увеличением амплитуды колебаний, вследствие нелинейной зависимости анодного тока от напряжения на сетке, поступающая в контур энергия уменьшится и при некоторой амплитуде колебаний сравняется с потерями. В результате устанавливается режим стационарных периодических колебаний, в котором все потери энергии компенсирует анодная батарея.

Выпишем уравнение таких колебаний

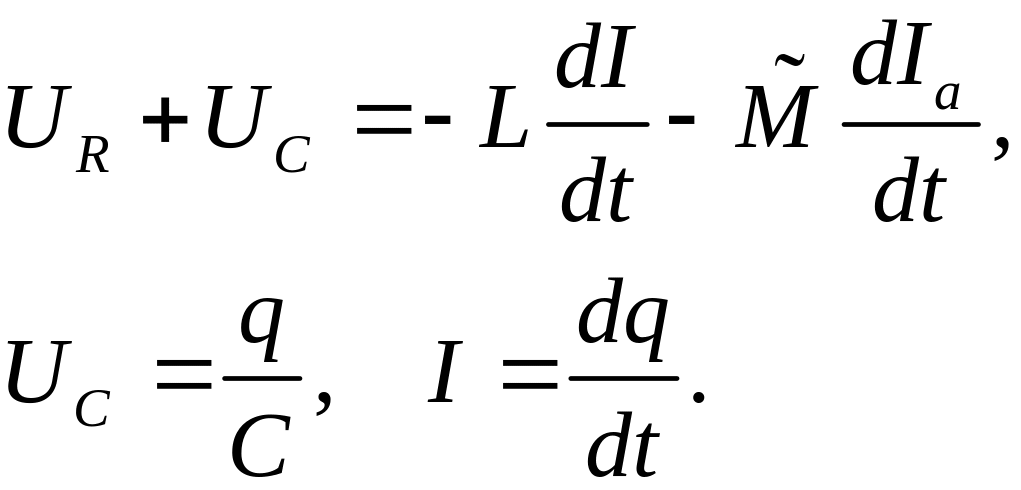(1)

Напряжение на сетке равно напряжению на конденсаторе

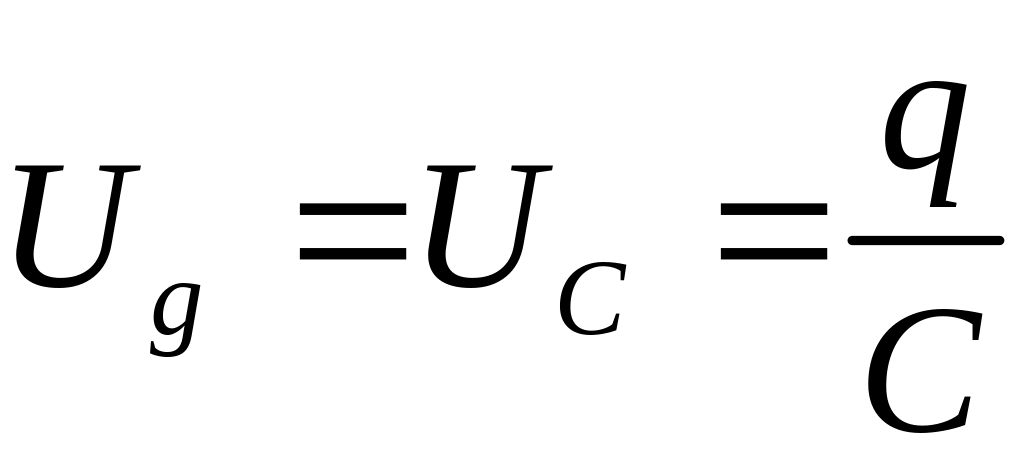, (2)

где - заряд на верхней обкладке конденсатора. Обозначим

. (3)

Далее имеем

, (4)

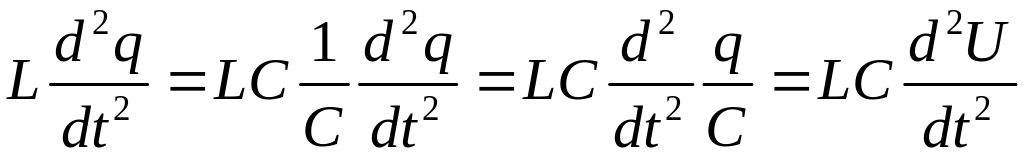. (5)

Отсюда находим

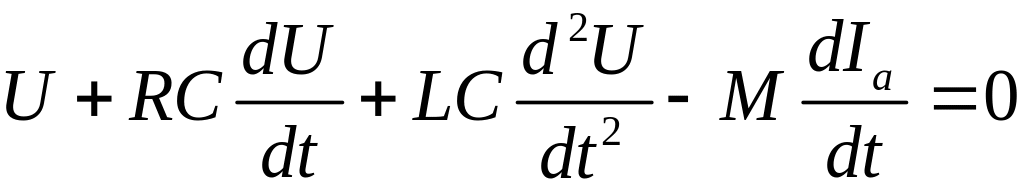. (6)

В реальных условиях в колебательном контуре всегда возникают колебания. Некоторая часть тока из колебательного контура ответвляется и идет на сетку. Так как емкость конденсатора велика по сравнению с емкостью между нитью и сеткой лампы, основной ток устремляется через конденсатор. Очевидно

. (7)

Так как сетка расположена значительно ближе к катоду, то изменение потенциала сетки значительно сильнее сказывается на величине анодного тока, чем равное изменение потенциала анода. Поэтому влиянием изменений анодного напряжения на анодный ток можно пренебречь. Тогда можно записать

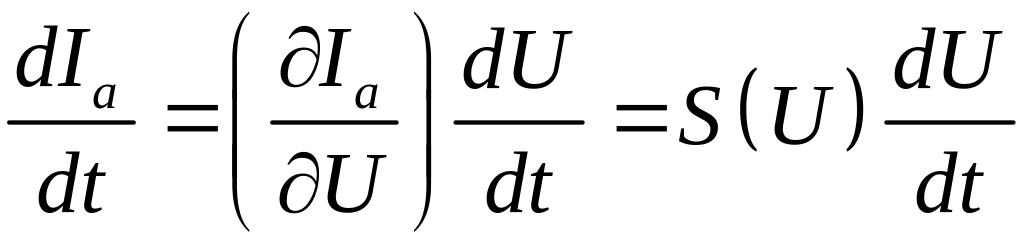. (8)

Величину называют крутизной сеточной характеристики. При изменении анодного тока в колебательном контуре генерируется э.д.с.

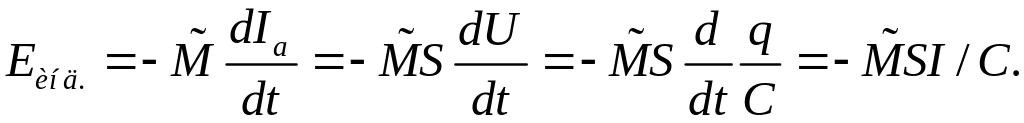(9)

Если , то имеют одинаковые знаки. В этом случае ток в контуре будет нарастать – произойдет самовозбуждение колебаний. Знак изменяется пересоединением концов катушки обратной связи.

Подставляя (8) в (6), получим уравнение

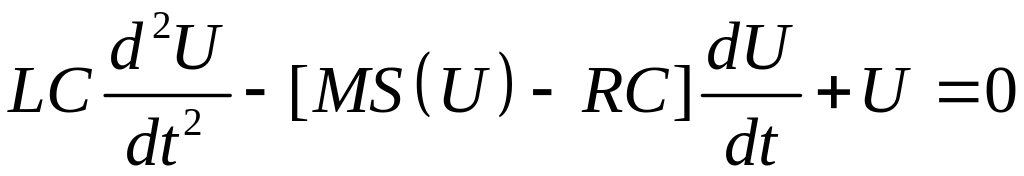. (10)

Уравнение (10) и есть искомое нелинейное уравнение лампового генератора.

Зависимость анодного тока от напряжения на сетке можно аппроксимировать следующим выражением

. (11)

Это означает, что

. (12)

Подставив (12) в (10), получим

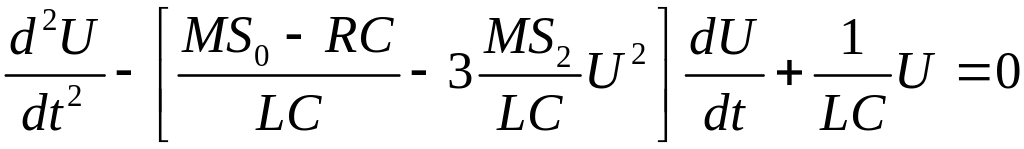. (13)

Уравнение (13) называется уравнением Ван-дер-Поля. Введем обозначения

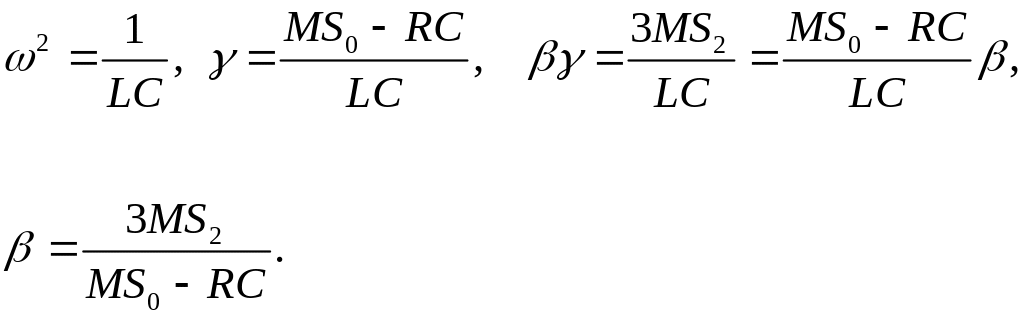
(14).

Тогда уравнение (13) принимает вид

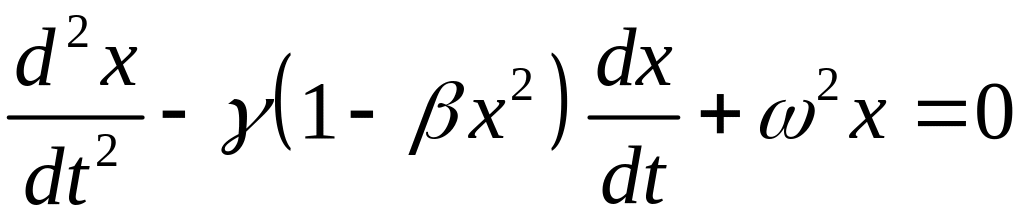. (15)

Уравнение (15) удобно еще представить в виде

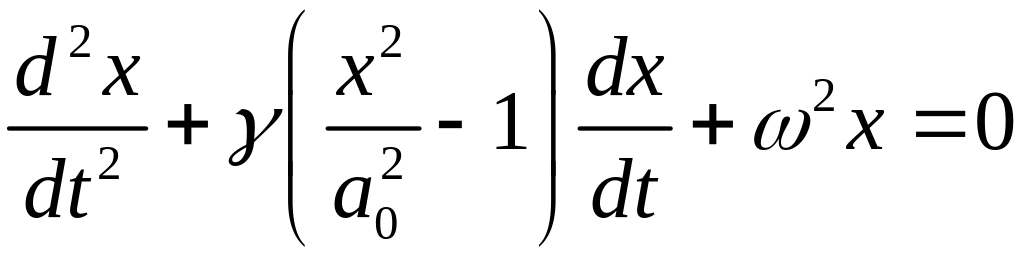. (16)

В такой форме уравнение Ван-дер-Поля выглядит как уравнение линейного осциллятора с нелинейной силой трения. При уравнение (16) переходит в уравнение линейного осциллятора. Решение (16) не может быть получено в аналитической форме. Найдем приближенное решение (16) при условии . В этом случае движение можно рассматривать как гармонические колебания с амплитудой, которая медленно изменяется со временем.

Введем переменные действие-угол по формулам для гармонического осциллятора

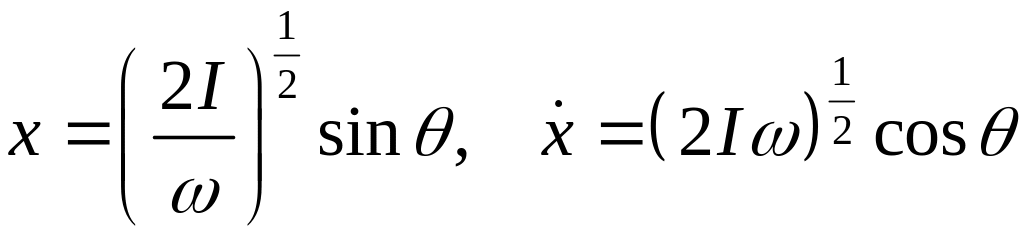. (17)

Отсюда находим

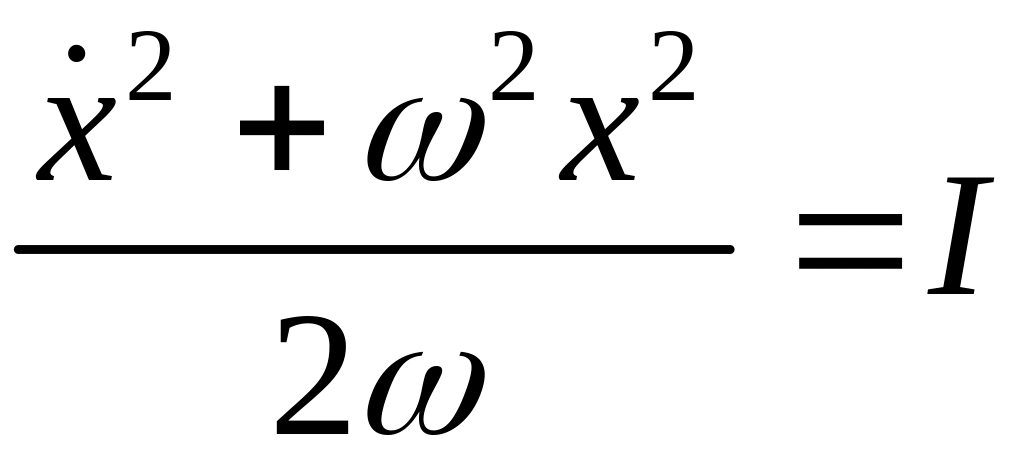. (18)

Аналогичное соотношение выполняется для гармонического осциллятора. Но в данном негамильтоновском случае величина не сохраняется со временем (система не является интегрируемой). Имеем

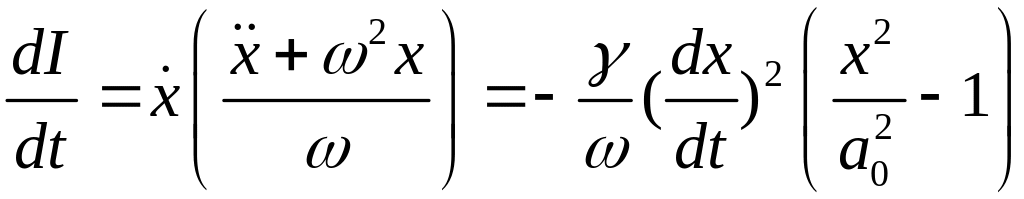. (19)

Целесообразно ввести величину

, (20)

которая является характерным действием в данной задаче. Тогда уравнение (19) принимает вид

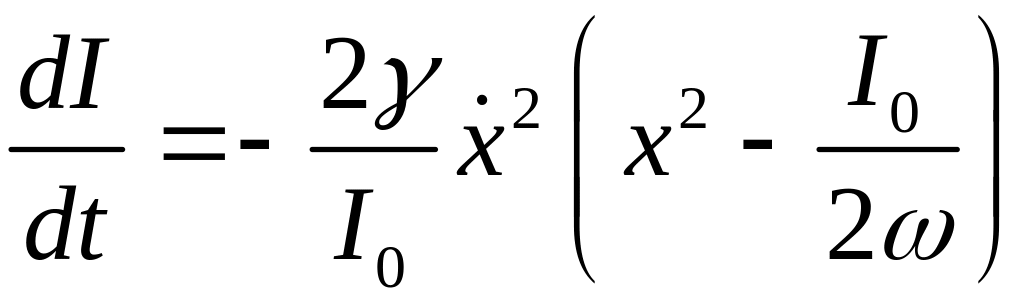. (21)

Теперь в (21) подставляем (17). Получим

. (22)

Получено дифференциальное уравнение, в котором величина изменяется относительно медленно по сравнению с величиной . Поэтому можно усреднить (22) по периоду быстрых колебаний. На малом периоде осцилляций величины 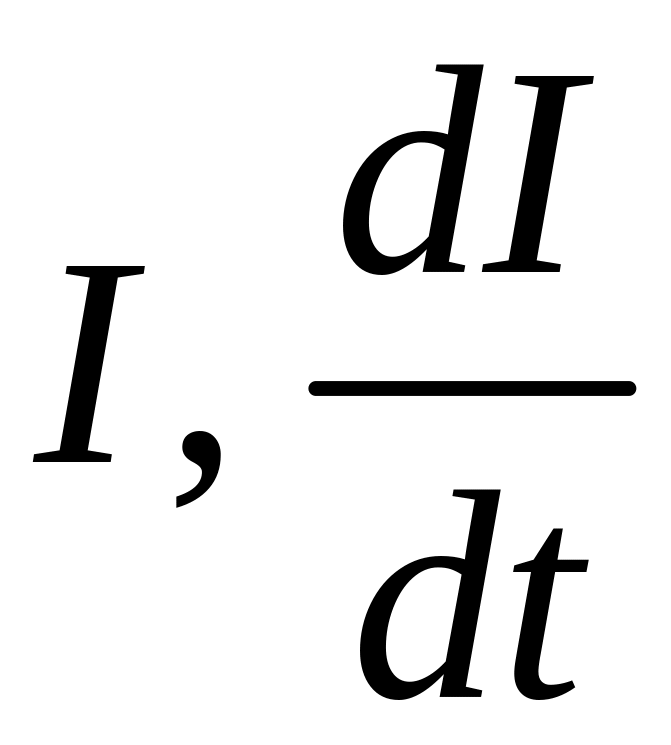практически не меняются и поэтому при усреднении они могут рассматриваться как постоянные. Имеем

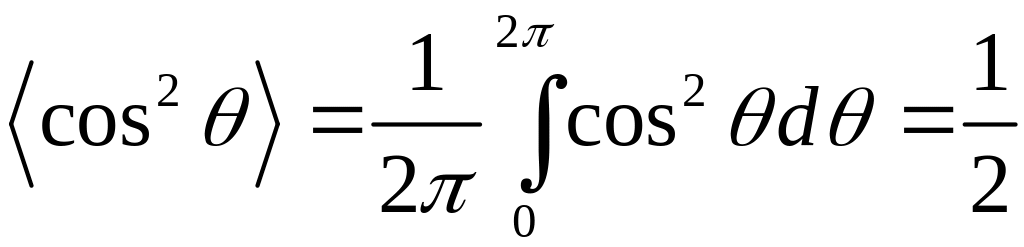. (23)

Далее

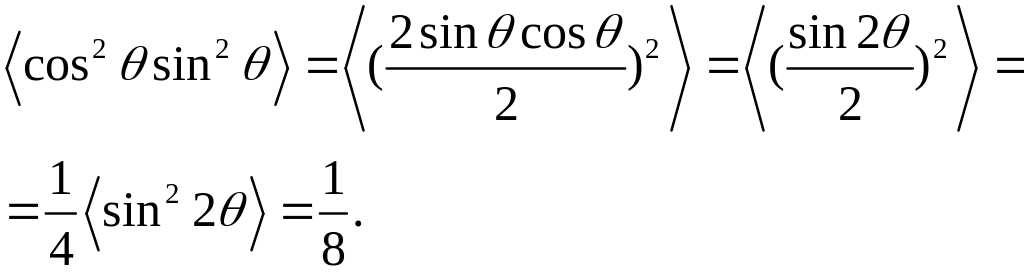(24)

После такого усреднения получаем

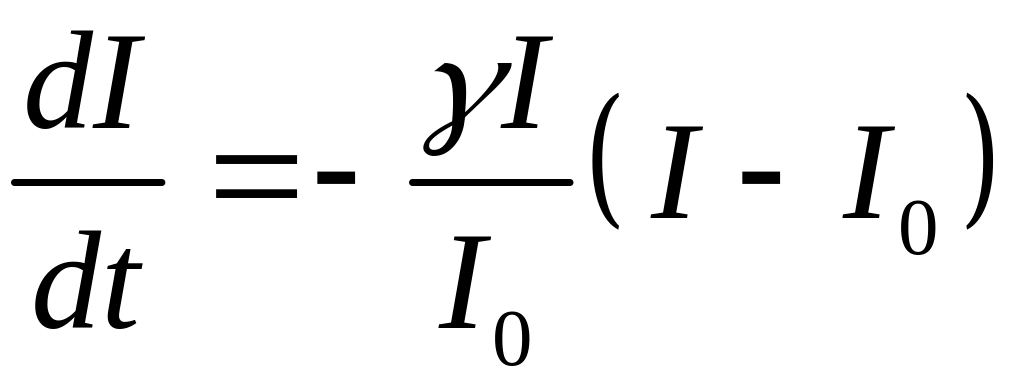. (25)

Имеются два положения равновесия , устойчивость которых проанализируем первым методом Ляпунова. Матрица линеаризации, состоящая в данном случае из одной клетки, имеет вид

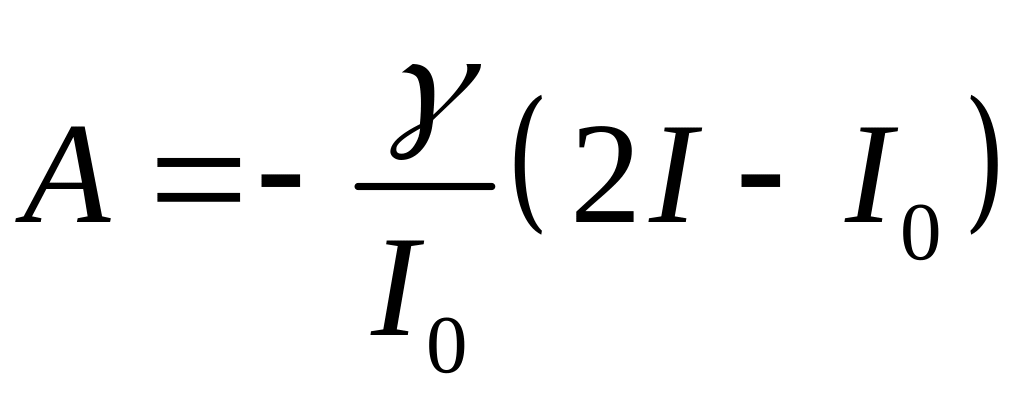, (26)

причем при

, (27)

а при

. (28)

Поэтому точка равновесия неустойчива, а точка равновесия устойчива. В переменных уравнение определяет окружность и в соответствии с проделанным анализом соседние траектории будут наматываться на эту окружность. Нелинейное уравнение (25) в данном простом случае имеет аналитическое решение. Разделяя переменные в (25), имеем

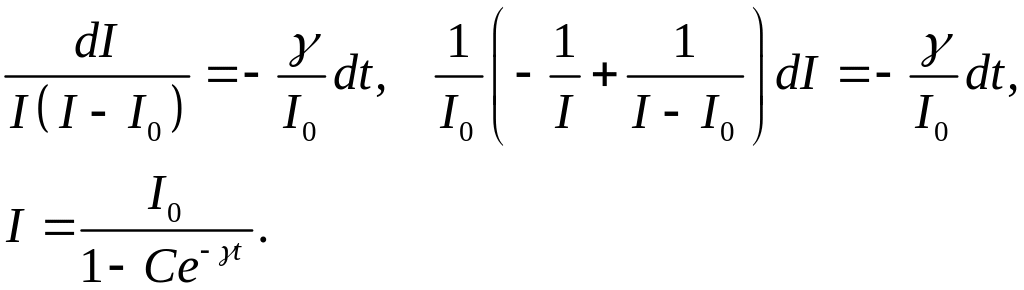(29)

Из полученного решения видно, что при любом значении С (постоянная интегрирования) соответствующая траектория при приближается к окружности . Это означает , что при любых начальных условиях (в определенных пределах) в данной системе возникают автоколебания. Полученные результаты позволяют изобразить картину фазовых колебаний и на фазовой плоскости . Из уравнений (17) имеем

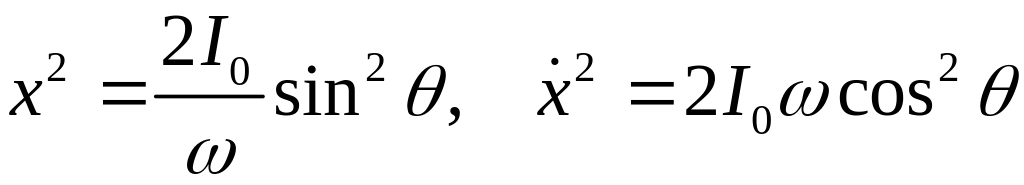. (30)

Отсюда получаем

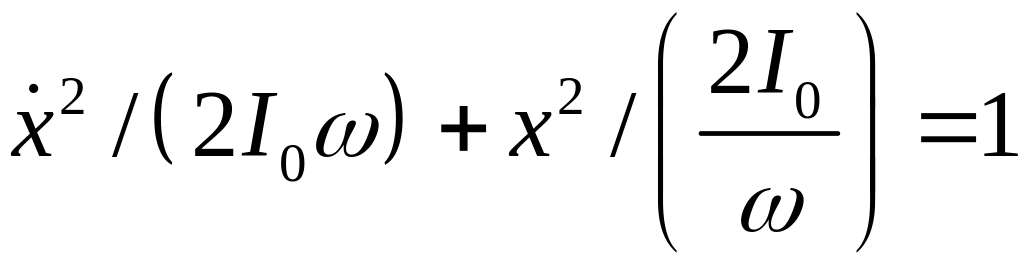. (31)

Это уравнение эллипса с полуосями 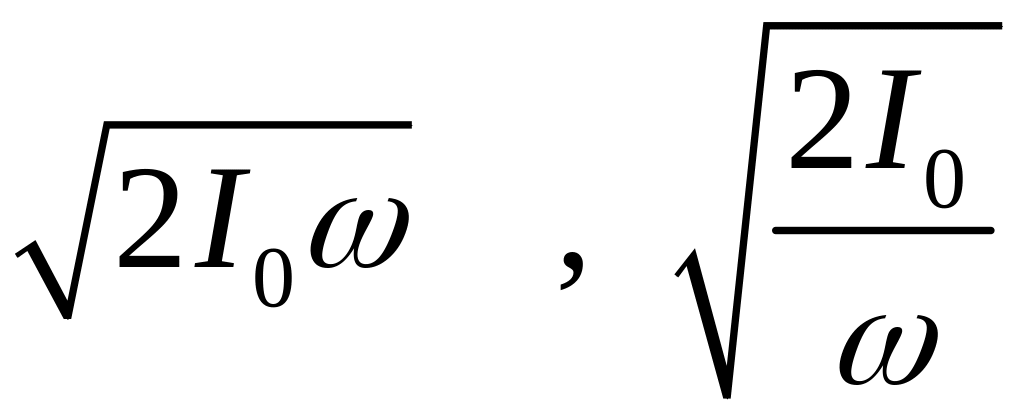. Площадь эллипса равна .

Т.о., особыми могут быть не только точки, но и замкнутые кривые. В диссипативном негамильтоновском случае существуют периодические движения с конечным периодом – циклы (предельные циклы). На фазовой плоскости им соответствуют замкнутые кривые, не проходящие через какие-либо особые точки. Циклы являются

предельными траекториями и особыми траекториями, на которые система никогда не выйдет ни за какой конечный промежуток времени и никогда не сойдет с нее, если находилась на цикле в начальный момент. В рассматриваемом случае режим возбуждения автоколебаний называется мягким. Для возбуждения таких автоколебаний достаточно наличие бесконечно малого возмущения, т.е. фактически не требуется начального толчка.

Для перехода систем с жестким самовозбуждением в режим стационарной генерации необходимо начальное возмущение с амплитудой, большей некоторого критического значения. Для выхода траектории на устойчивый предельный цикл начальная точка на фазовой плоскости должна лежать вне области притяжения устойчивого состояния равновесия.