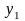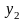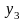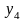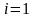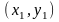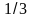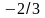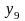№5 Исследование байесовского правила классификации в распознавании образов при непрерывных информативных признаках (условные плотности известны с точностью до параметров) и без обучающей выборки.

Цель работы: исследование решающего правила классификации при условиях:

• Имеется два независимых непрерывных информативных признака и неизвестно сколько классов;

• Априорные вероятности классов неизвестны;

• Все условные плотности вероятности (при условии истинности того или иного класса) для информативных признаков одинаковы и известны с точностью до параметров :

;

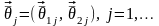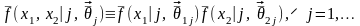• обучающая выборка неизвестна. Имеется обыкновенная выборка объёма .

Как видно из условий задача очень похожа на уже рассмотренную в пункте 4.1 задачу, но эта ситуация более сложная и к тому же более распространенная на практике Необходимо построить самообучающуюся систему классификации.

Рассмотрим один из вариантов.

П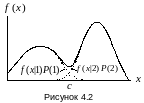 о количеству максимумов мы можем определить количество классов.

По количеству минимумов и их положению мы можем определить границы классов, что позволит произвести разбиение исходной выборки на две части и тем самым свести практически свести ситуацию к задаче, описанной в пункте 4.1.

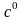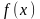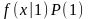Далее строится процедура последовательного (итерационного) расчета порога (в многомерном случае – разделяющей поверхности) . Например, задается нулевое приближение порога . Оно разбивает исходную выборку (по которой оценивалась безусловная плотность на две части. Выборка становится обучающей. По ней (как было рассмотрено выше) оцениваются условные взвешенные плотности и 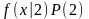, а следовательно, решающая функция и новое приближение порога 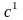(разделяющей поверхности) и т. д.

Возможны и другие пути самообучения.

Например для моделирования этой ситуации вы можете взять два класса (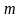 = 2), один информативный признак и условные плотности 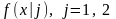, – это нормальные законы распределения:

, .

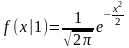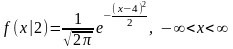Если законы имеют одинаковую единичную дисперсию и отличаются математическими ожиданиями: 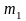= 0, 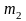= 4, то итоговые плотности распределения 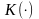информативного признака 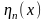при различных значениях априорных вероятностей классов и 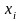приведены на рис. 4.3.

При реализации расчетно-графической работы необходимо варьировать: количество классов, математические ожидания и априорные вероятности классов.

Для наглядной демонстрации реализованная программа должна выводить графики похожие на те, что приведены на рисунке 4.3.

5. Планирование эксперимента Исследование алгоритмов построения степенных моделей с использованием ортогональных планов первого и второго порядков

Цель работы: исследование алгоритмов планирования эксперимента при построении степенных моделей первого и второго порядка.

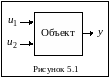
Объект исследования (рисунок. 5.1) имеет два входа 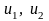и один выход 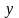. Основная проблема планирования эксперимента состоит в создании таких планов покачивания входных переменных (при снятии экспериментальных данных [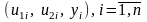 ] с объекта), которые обеспечивают более быстрое и точное построение модели объекта. Выход объекта состоит из неизвестного сигнала (здесь 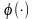– неизвестная функции от входов, называемая поверхностью отклика) и центрированной аддитивной помехи ( ).

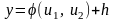
Модель первого порядка:

,

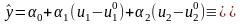
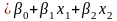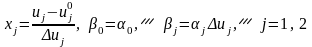
Модель второго порядка:

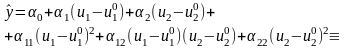
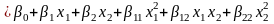
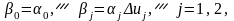
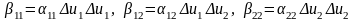
Здесь 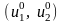– базовая точка.

Измерения выхода объекта некоррелированные равноточные.

Расчёт параметров 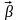моделей первого и второго порядков в безразмерных переменных проводится по методу наименьших квадратов.

№6 Построение линейной модели.

Итак, модель имеет вид:

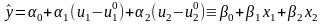
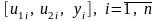Необходимо на основе эксперимента: ) вычислить коэффициенты 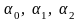модели.

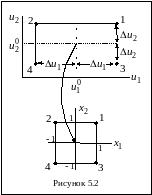
Экспериментальные точки для входных координат зададим в вершинах гиперпрямоугольника. Точки такого плана для 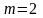показаны в верхней части рис. 5.2. Эти точки равномерно распределены относительно известной базовой точки .

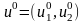Интервалы покачивания 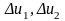относительно базовой точки задаются экспериментатором, и они определяют область изучения объекта. Для этой области и строится линейная модель.

С целью унификации процедур построения планов, исследования их свойств, расчета параметров и исследования качества модели осуществляется переход от размерных входных переменных к безразмерным :

.

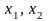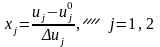Точки плана в вершинах прямоугольника (верхняя часть рисунка 4) в новых координатах оказываются в вершинах квадрата с единичными координатами (нижняя часть рисунка. 5.2). Центр плана переходит в начало координат. Полученный план представлен в табл. 5.1. В этом плане кроме безразмерных входных переменных 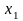, 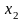введены столбец фиктивной переменной 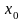и столбец измерений выхода объекта в каждой точке плана. Фиктивный столбец состоит из +1 и служит для симметрии расчета всех коэффициентов модели. Для упрощения записи плана единица опускается и указывается только знак единичной координаты.

Таблица 5.1

1	+	+	+
2	+	–	+
3	+	+	–
4	+	–	–

В новых безразмерных координатах линейная модель также сохраняет линейный вид:

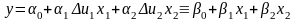
Из этого уравнения следует алгоритм расчета коэффициентов 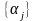по коэффициентам :

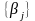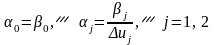
Параметры 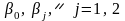модели рассчитаем по критерию наименьших квадратов

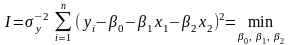
предполагая, что измерения выхода 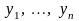некоррелированные и равноточные с дисперсией 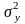. Из этого критерия следует система линейных алгебраических уравнений:

,

,

.

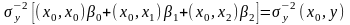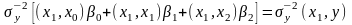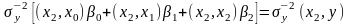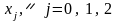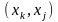Здесь – столбцы матрицы планирования, включая фиктивный столбец , состоящий из "плюс единиц", – столбец измерений выхода объекта; и 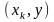– скалярные произведения столбцов матрицы планирования:

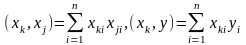
Если реализован план, представленный в табл. 5.1, то векторы-столбцы 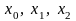взаимно ортогональны, т. е. 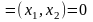. Система уравнений распадается на независимые уравнения, из которых вычисляются параметры модели:

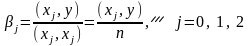
Здесь учтено, что скалярные произведения векторов самого на себя одинаковы и равны количеству измерений.

Корреляционная матрица 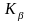для параметров, удовлетворяющих критерию наименьших квадратов, равна матрице, обратной матрице системы алгебраических уравнений для :

= =

= =

= =

= .

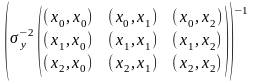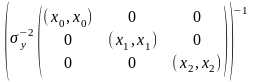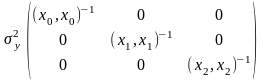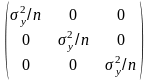Параметры некоррелированные и дисперсия их одинакова:

.

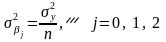Дисперсия выхода линейной модели

, .

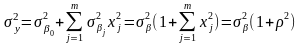одинакова на равном расстоянии от центра плана, т. е. ортогональный план первого порядка является и ротатабельным.

Проверим адекватность модели. Вычисляем остаточную сумму квадратов , делим ее на число степеней свободы 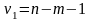и получаем остаточную дисперсию (дисперсию адекватности):

.

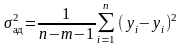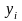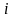Здесь – выход объекта в -й точке эксперимента, – выход модели в той же точке. При хорошем описании с помощью модели сигнальной части выхода объекта остаточная дисперсия оценивает дисперсию выхода объекта.

Плохо, что у остаточной дисперсии только одна степень свободы 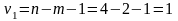. Вынести гарантированное решение с помощью такой «плохой» оценки нельзя. Для улучшения итогового решения об адекватности модели надо увеличить число степеней свободы оценки за счёт проведения в каждой точке плана нескольких (3–5) измерений. Коррекцию формул расчёта проведите самостоятельно.

На основе дополнительного эксперимента объема 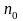в центре плана строим оценку для дисперсии выхода объекта. Число степеней свободы для оценки равно величине .

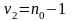Далее по статистике Фишера 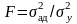проверяется гипотеза о равенстве дисперсий. Эта гипотеза совпадает с гипотезой об адекватности модели. Если статистика 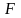не превосходит порогового значения 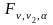, то принимается гипотеза об адекватности модели. В противоположном случае эта гипотеза отвергается. Тогда надо заново строить модель, например, усложняя ее за счет введения дополнительных факторов, либо отказываться от линейной модели и переходить к построению квадратичной модели.

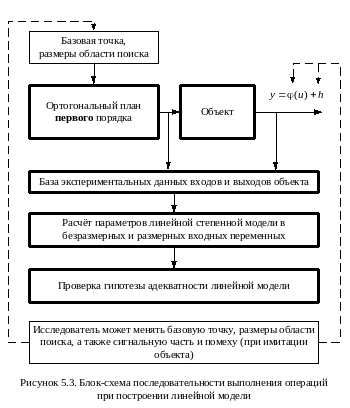
Блок схема последовательности выполнения операций приведена на рис. 5.3.

№7. Построение квадратичной модели.

При построении более сложной квадратичной модели 2-го порядка

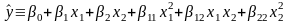
Используем композиционный ортогональный (при этом 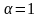) план Бокса – Уилсона – см. таблицу 5.2. Здесь же показана замена столбцов с квадратичными переменными 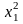, 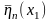соответствующими столбцами , .

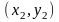Все элементы каждого столбца , отличаются от соответствующих элементов столбцов , на свою постоянную величину (среднее арифметическое):

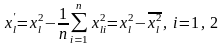
Таблица 5.2

1	+	+	+	+	+	+
2	+	–	+	–	+	+
3	+	+	–	–	+	+
4	+	–	–	+	+	+
5	+	+	0	0	+	0
6	+	–	0	0	+	0
7	+	0	+	0	0	+
8	+	0	–	0	0	+
9	+	0	0	0	0	0

В новых переменных все столбцы , , , , , ортогональны.

С учетом новых переменных имеем следующее уравнение модели:

.

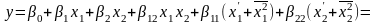
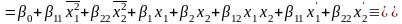
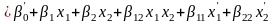Здесь .

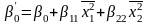План реализуется на объекте – см. таблицу 5.3. Например, в точке 5 плана 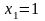, , 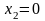что соответствует реальным входным переменным: 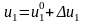, 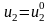. Реализуем эти значения входов на объекте и измеряем значение выходной переменной .

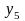Таблица 5.3

1	+	+	+	+
2	+	–	+	–
3	+	+	–	–
4	+	–	–	+
5	+	+	0	0
6	+	–	0	0
7	+	0	+	0
8	+	0	–	0
9	+	0	0	0

Параметры 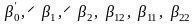в силу ортогональности плана вычисляются независимо (так же как и при использовании ортогонального плана первого порядка):

,

, ,

,

, .

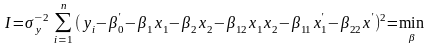
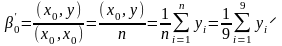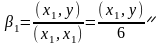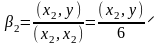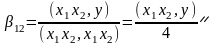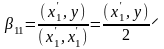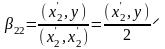Параметры некоррелированные и дисперсии их различны:

, , , .

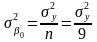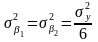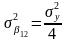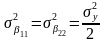В заключение остается пересчитать коэффициент

,

который оценивает сигнальную часть выхода объекта в центре плана.

В итоге построена модель второго порядка:

, , ,

, , .

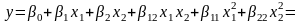
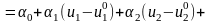
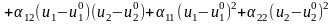
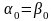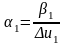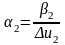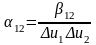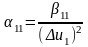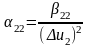Адекватность модели проверяется по той же схеме, как и для линейной модели. Соответствующие формулы выпишите самостоятельно.

Блок схема последовательности выполнения операций при построении квадратичной модели приведена на рис. 5.4.

При исследовании алгоритмов построения моделей естественно используется имитация объекта.

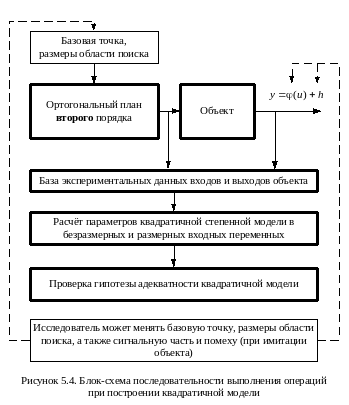
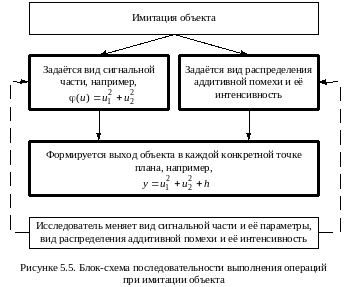
На рисунке 5.5 приведена блок-схема последовательности выполнения операций при имитации объекта.

Интенсивность помехи берётся по отношению к интенсивности сигнальной части. Показатели интенсивности и относительную величину интенсивностей Вы должны выбрать самостоятельно и использовать при установлении соответствующих закономерностей.

Приведённые ранее блок-схемы помогут Вам составить и выполнять план исследований.