1. Общая задача ЛП: максимизировать (минимизировать) целевую функцию (ЦФ) Y вида

при ограничениях:

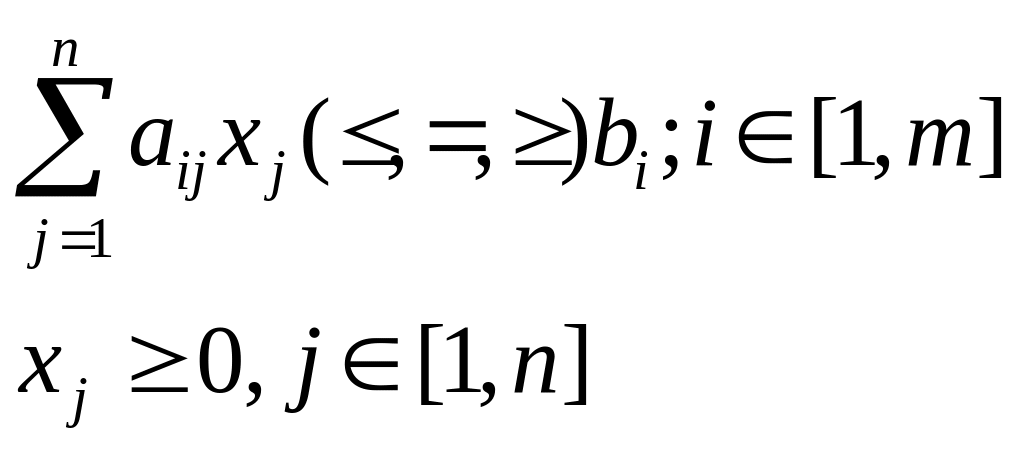
Экономическая интерпретация ЛП.

Моделируемая система характеризуется наличием j видов производственной деятельности, ,

Для осуществления которых требуются имеющиеся в ограниченном количестве ресурсы .

Расход с ресурса на единицу продукта j вида производственной деятельности равен , в результате осуществления производственной деятельности от каждого вида продукта получается прибыль .

Цель построения модели ЛП состоит в определении объемов производства каждого вида деятельности , при которых не нарушались бы ограничения на используемые ресурсы и достигался бы оптимум суммарной деятельности.

Основными допущениями моделей ЛП являются:

- пропорциональность

- аддитивность

- неотрицательность

Пропорциональность означает, что затраты ресурсов на некоторый вид производственной деятельности, а также вклад этого вида производственной деятельности в ЦФ прямопропорциональны его уровню.

Аддитивность означает, что общая величина ресурсов, потребляемых в системе всеми видами производственной деятельности равна сумме затрат ресурсов на отдельные виды производственной деятельности.

Оба эти ограничения обеспечивают строгую линейность соответствующих функций, и хотя на практике реальные зависимости линейными бывают крайне редко, данные допущения позволяют создать эффективные в вычислительном плане методы решения.

Неотрицательность означает, что ни одному из видов производственной деятельности не может быть приписан отрицательный уровень. В отличие от предыдущих, данное ограничение является логичным и соответствует большинству задач. Исключением, например, является задача целевого программирования, для которой не все ограничения могут выполняться одновременно.

Пусть ограничения заданы в стандартном виде:

В основе модели целевого программирования лежит допущение о возможности несоблюдения некоторых ограничений. Это обеспечивается введением некоторых функций штрафа. Для этого в левую часть ограничений вводят неограниченную в знаке переменную . Наиболее эффективным является определение:

Хотя ЛП ориентировано на статические задачи, соответствующие модели формируются и для динамических задач, в частности для тех, где рассматривается несколько последовательных интервалов времени и результат предыдущего является исходными данными для следующего (задачи планирования производства). Другое приложение динамических задач – представление коэффициентов моделей, как функции некоторых параметров. Моделями ЛП могут представляться и стохастические задачи. Это возможно, если известны вероятностные характеристики всех параметров (мат. ожидание, дисперсия.).

Примером такой задачи является транспортная задача, при условии что спрос на местах задается как случайная величина.

Даже если для практической задачи модель не удается представить в виде линейной (даже с учетом аппроксимации) модель ЛП используется для получения методов решения нелинейных задач.

2. Типичные задачи лп.

Транспортная задача.

Предназначена для выбора наиболее экономного плана перевозок товаров из m источников в n пунктов назначения. Возможная величина поставки от i поставщика равна , спрос на товар в j равен . Стоимость перевозки из i в j равна .

Формулировка: минимизировать ЦФ

при ограничениях: .

Большинство методов решения таких задач ориентировано на обеспечение условия

Если это условие на практике не выполняется, то его обеспечивают вводя фиктивный источник ил фиктивный пункт сбыта.

Транспортная задача с промежуточными пунктами.

Является расширением предыдущей задачи и допускает существование промежуточных транспортных узлов. При этом, прежде чем попасть на конечную станцию, все товары ил часть из них могут транзитом следовать через другие источники или пункты сбыта. Данные условия учитывают, рассматривают расширенную транспортную сеть с n+m источниками и n+m пунктами сбыта. При этом объекты поставок от каждого источника и размеры спроса в каждом пункте сбыта увеличивают на величину некоторого буферного запаса B:

Тогда величина поставок от источника i равна:

Аналогично для каждого j пункта сбыта величина поставок равна:

Удельная стоимость определяется исходя из условий задачи.

Одним из вариантов транспортной задачи является задача о поставщике. Поставщик имеет контракт на n дней например на снабжение чистыми салфетками. Он может поставлять либо новые салфетки, либо стирать и гладить старые. Стирать и гладить дешевле, однако он не всегда это успевает. Цель: выполнить контракт при минимальных затратах.

Задача о назначениях.

Существует m исполнителей и n работ, причем эффективность каждого исполнителя на работах различна. Особенность: , т.е. на работу может быть назначен один исполнитель и наоборот.

Стоимость .

Методы решения таких задач могут непосредственно использоваться при решении задачи о коммивояжере.

Обобщенная транспортная задача.

Минимизировать ЦФ вида:

при ограничениях:

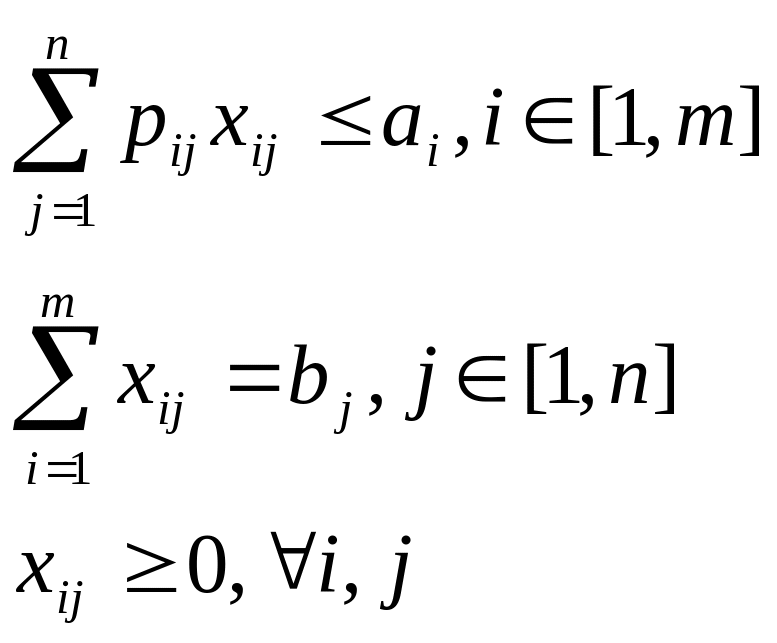
Одно из известных приложений данной задачи связано с распределением различных типов самолетов по разным авиалиниям, с тем, чтобы удовлетворить потребности пассажиров при минимальном уровне эксплуатационных расходов. - максимальное число пассажиров на авиалинии вида i. - число имеющихся самолетов вида j. - допустимое число пассажиров для одного самолета вида j на линии i. - эксплуатационные расходы, приходящиеся на один самолет типа j на авиалинии вида i. Требуется найти значение , которое будет обозначать количество самолетов вида j на лини вида i.

3. Классификация распределительных задач.

1. По виду ЦФ:

- линейные

- нелинейные

Если затраты (доход), определяемые объемом ресурса i, выделенного на выполнение работы j равны и ограничения линейны, то имеем линейную распределительную задачу (иначе нелинейную).

2. По имеющимся в наличии потребным ресурсам:

- сбалансированные (закрытые)

- несбалансированные (открытые)

Задача называется сбалансированной, если имеет место равенство: ,

иначе задача несбалансированная.

При этом, если имеет место знак ≤, решают, какие работы не выполнять, если ≥, то какие ресурсы не использовать.

3. По характеру изменения переменных:

   • Задачи с непрерывным изменение переменных, т.е. любая переменная принимает любое значение.

   • Задачи с целочисленными переменными (и неотрицательными)

   • Дискретная задача распределения, если в результате решения допустимо использовать заданное конечное множество переменных.

4. По количеству экстремумов ЦФ:

   • Одноэкстремальные.

   • Многоэкстремальные.

Одноэкстремальные задачи – это задачи, в которых любой локальный оптимум одновременно является и глобальным.

5. По характеру распределения ресурсов во времени:

   • Статические.

   • Динамические.

4.

Формулировка.

В таких задачах обычно принимают m = n. Имеется n работ и n кандидатов. Назначение i кандидата на j работы связано с некоторыми затратами . Требуется найти назначения кандидатов на все работы, дающие минимальные суммарные затраты. Одного кандидата можно назначить на одну работу и наоборот.

Задача.

Имеется 4 крана и требуется выполнить монтаж 4-х объектов, при этом известно какое время необходимо крану на монтаж объекта . Необходимо распределить краны по объектам так, чтобы суммарное время на монтаж этих объектов было минимальным, при этом - затраты времени i крана на монтаж j объекта.

Т1

	3	7	5	8	1	3
	2	4	4	5	1	2
	4	7	2	8	1	2
	9	7	3	8	1	3
	1	1	1	1

Введем переменные:

П усть

Решение.

Одним из наиболее распространенных и эффективных является Венгерский метод. Оптимальность решения задачи о назначении не нарушается при уменьшении (увеличении) элементов строки (столбца) на одну и туже величину ( ). Решение считается оптимальным если все измененные искусственно затраты и можно найти такой набор , что ЦФ вида:

Алгоритм метода.

1. Получение нулей в каждой строке

T2

	0	4	2	5	1
	0	2	2	3	1
	2	5	0	6	1
	6	4	0	5	1
	1	1	1	1
	0	2	0	3

T3

	0*	2	2	2	1
	0	0*	2	0	1
	2	3	0*	3	1
	6	2	0	2	1
	1	1	1	1

Для этого находим наименьший элемент каждой строки и вычитаем его из всех элементов этой строки. Аналогично поступают и с каждым столбцом

2. Поиск оптимального решения.

Рассматривают одну из строк Т3, имеющую меньшее количество нулей, отмечают * один из них, и затем зачеркивают все остальные нули этой строки и того столбца, в котором находится этот нуль. Аналогичные действия проводят для всех строк. Если назначения, которые получены при всех нулях, отмеченных * являются полными, т.е. количество этих нулей n, то решение является оптимальным. В противном случае, необходимо перейти к следующему этапу.

3. Поиск минимального набора строк и столбцов, содержащих нули.

Для этого необходимо отметить * следующее:

1. Все строки, в которых не имеется ни одного, отмеченного * нуля.

2. Все столбцы, содержащие перечеркнутый ноль хотя бы в одной из отмеченных * строк.

3. Все строки, содержащие отмеченные * нули хотя бы в одном из отмеченных * столбцов.

Действия b) и c) повторяются поочередно, пока есть что отмечать.

После этого необходимо зачеркнуть каждую непомеченную строку и каждый помеченный столбец.

Цель этого этапа – провести минимальное число горизонтальных и вертикальных линий, пересекающих по крайней мере один раз все нули.

4. Перестановка некоторых нулей.

Т4

	0*	2	4	2	1
	0	0*	4	0	1
	0	1	0*	1	1
	4	0	0	0*	1
	1	1	1	1

Берут наименьшее число из тех клеток, через которые не проведены прямые, вычитают его из каждого числа вычеркнутых столбцов и прибавляют к каждому числу вычеркнутых строк в вычеркнутых столбцах.

Эта операция не изменяет оптимального решения. После этого переходят к этапу 2.

В Т4 число нулей, отмеченных * равно n, следовательно назначение является полным, а решение оптимальным. Клетки со * указывают объект монтажа для каждого крана.

Решение (оптимальное) может оказаться не единственным, однако для всех этих решений значение ЦФ будет одинаково.

5-6. Транспортная задача.

В общем виде формулируется так:

Имеется m пунктов отправления (пунктов производства) и n пунктов назначения (потребления). Обозначим ресурсы груза в i пункте отправления через , а потребность каждого j пункта потребления через ,

Задана стоимость перевозки единицы груза от каждого i пункта отправления до каждого j пункта потребления и равна . Требуется определить какое количество груза необходимо перевести из в , чтобы при этом:

• Вывести грузы всех поставщиков.

• Удовлетворить всех потребителей.

• Достигнуть экстремума ЦФ.

Задача.

Пусть в городе имеется 4 ДСК (домостроительных комбината: ) и строится 4 микрорайона ( )Известны производственные мощности ДСК и потребность комплектов изделий каждого микрорайона. Известны также приведенные затраты, связанные с доставкой одного комплекта с каждого ДСК в каждый микрорайон.

Т5

	70	38	24	92	14
	58	18	56	72	20
	19	10	100	30	26
	3	36	121	8	41
	30	22	15	34

Обозначим через и ресурсы отправителей и потребности получателей соответственно.

Транспортные задачи могут быть сбалансированными (закрытыми) и несбалансированными (открытыми).

- задача сбалансированная.

Пусть в нашем случае задача сбалансированная, причем =

Чтобы вывести грузы всех поставщиков необходимо выполнение следующего равенства:

,

Аналогично, чтобы удовлетворить всех потребителей необходимо:

,

Решением задачи является нахождение таких значений , которые минимизируют ЦФ вида:

.

Исследование полученной модели.

Решение транспортной задачи как правило проводят в 2 этапа. Первый этап называется отысканием опорного (начального плана). На втором этапе производится последовательное улучшение опорного плана по определенным условиям (методам) до тех пор, пока дальнейшее улучшение не станет невозможным. От того, какой будет опорный план зависит время решения задачи на втором этапе.

Наиболее эффективным методом нахождения опорного плана является метод аппроксимации Фогеля. В большинстве случаев этот метод дает опорный план наиболее близкий к оптимальному, а иногда сразу оптимальный, поэтому его рекомендуют для расчета по матрицам большого объема.

В основе метода лежит концепция штрафов, взимаемых за выбор не самого оптимального транспортного маршрута. Штраф по каждой строке и каждому столбцу определяется из анализа маршрутов и различными показателями издержек как разность двух различных уровней транспортных издержек. При этом первой заполняется клетка таблицы, в которой фиксируется самый крупный штраф. После ее заполнения штрафы пересчитываются и так до тех пор, пока все ресурсы не будут распределены.

Алгоритм метода.

1) Вычисление разностей в каждой строке и каждом столбце таблицы между наименьшей стоимостью и ближайшей к ней по величине. Разности по строкам записываются справа в столбцы разностей., разности по столбцам в низу в строки разностей.

2) Поиск из всех разностей как по строкам, так и по столбцам максимальной.

3) Размещение в клетку, где находится наименьшая стоимость максимально возможного количества ресурсов.

4) Вычисление разностей по строкам и по столбцам не принимая во внимание стоимости в клетках, имеющих ресурсы и в клетках с *. Опять определяется максимальная разность в строках и столбцах.

5) Поиск минимального элемента в строке или столбце с максимальной разностью и размещение в данную клетку максимально возможного (с учетом потребностей) количества ресурсов, после чего возвращаемся к этапу 4 и т.д.

После получения опорного плана переходят ко 2 этапу решения транспортной задачи, который предусматривает последовательное улучшение полученного плана.

Существует несколько методов последовательного улучшения опорного плана, рассмотрим метод потенциалов.

Метод имеет в своей основе вычисление критерия оптимальности вида:

-затраты связанные с доставкой одной единицы ресурса из пункта отправления в пункт назначения.

- расчетные затраты, связанные с доставкой единицы ресурса из в , определяемые для тех клеток опорного плана, ресурсы в которых нераспределены.

Если все , то существующий опорный план оптимален. Если нет, то опорный план улучшим методом потенциалов.

						Столбцы разностей
	70 *	38 *	24 14	92 *	14	14	14	-	-	-
	58 *	18 20	56 *	72 *	20	38	-	-	-	-
	19 23	10 2	100 1	30 *	26	9	9	9	11	-
	3 7	36 *	121 *	8 34	41	5	5	5	5	-
	30	22	15	34
Строки разностей	16	8	32	22
	16	26	76	22
	16	26	21	22
	16	-	-	22
	16	-	-	-

Метод потенциалов.

Алгоритм метода.

1. Составление и решение системы уравнений.

Где , -переменные, индексы , которых при пересечении соответствуют клетке, для которой ресурсы распределены.

Имеем 7 уравнений, 8 неизвестных. Для решения системы наиболее часто встречающейся переменной присваиваем произвольное значение (для облегчения счета обычно присваивают значение 0) = 0

Решая последовательно соответствующие уравнения получим:

2. Определение значений .

При этом используются те индексы , , на пересечении которых в соответствующих клетках ресурсы не распределены.

3. Определение значения критерия оптимальности :

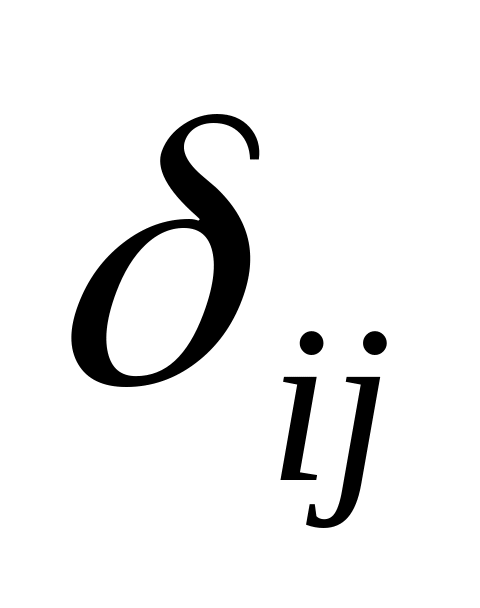и проверка условия оптимальности.

Если все , то план оптимален.

Если хотя бы один , то переходят к новому опорному плану.