2. Порядок виконування роботи :

2.1. Уважно розібрати методичні вказівки до практичної роботи.

2.2. Уважно розглянути умови задач 1 та 2 та розібрати їх рішення

2.3. Вирішити завдання

2.4. Оформити та захистити звіт

3. Методичні вказівки до практичної роботи.

Статистичний аналіз за допомогою великої вибірки

Статистичний аналіз за допомогою великої вибірки полягає в наступному.

З верстата береться велика (поточна) вибірка, що складається з деталей, виготовлених підряд одна за іншою при незмінної настройці верстату та незмінних

умовах обробки. Обсяг вибірки встановлюється в залежності від бажаної точності і надійності визначення розсіювання  сумарної погрішності обробки. Для цього варто використовувати методику, викладену в роботі [ 2 ]. Для практичних цілей можна прийняти точність обчислення оцінки  по вибірковому S (  =  0.2 S )

з ймовірністю  = 0,95. Тоді обсяг вибірки досить зробити рівним n = 50. Однак зі збільшенням n точність  зростає і тому часто приймають n  100.

Усі деталі вибірки повинні бути обмірювані шкальним вимірювальним інструментом з ціною розподілу вимірювальної шкали, рівної ( 1/6  1/10 ) Т, де Т - допуск на вимірюваний розмір.

На підставі результатів вимірів деталей вибірки складається таблиця розподілу розмірів вибірки.

При складанні таблиці всі розміри, що спостерігаються, розбиваються на інтервали, число яких вибирається так, щоб ширина інтервалу була більшою не менш чим у 2 рази ціни розподілу шкали вимірювального інструмента. Це робиться для того, щоб компенсувати погрішності виміру. Потім обчислюються статистичні характеристики вибірки і S, що і приймаються як оцінки параметрів ₀ і ₀ розподілу генеральної сукупності, з якого узята вибірка, Після цього робиться перевірка гіпотез нормальності і випадковості вибірки [ 2 ]. При позитивних результатах цієї перевірки сумарна погрішність обробки визначається за формулою

(1)

де n, с - відповідно постійні та випадкові погрішності.

Для визначення сумарної величини випадкових погрішностей у всієї настроєної партії необхідно як оцінку σ₀ прийняти σ = SZ₂, де S - середнє квадратическое відхилення вибірки, а Z₂ – коефіцієнт залежності від обсягу вибірки ( таблиця 10 додатку ). Тоді

(2)

Фактична величина постійних погрішностей Δ_п чи резерв допуску, що приходиться на частку постійних погрішностей, визначається по наступних формулах;

а) для зовнішніх поверхонь

(3)

б) для внутрішніх поверхонь

(4)

де ES і ei – верхнє і нижнє граничні відхилення вимірюваного розміру з урахуванням їх знаків;

- середнє значення відхилень розмірів від їхнього номіналу.

Для оцінки точності процесу необхідно порівняти отриману сумарну погрішність Δ с допуском T на розмір деталі.

Точність процесу вважається достатньої чи надлишкової, якщо задоволь-няється нерівність (5)

Однак на практиці брак можливий навіть і при надлишковій точності процесу, якщо настроювання верстата було виконано з погрішністю, величина якої перевищила припустиме значення.

Позначимо через координату середини полю допуску щодо номінального значення розміру, величина якої визначається по формулах:

; (6)

, (7)

де es і ei - верхнє і нижнє відхилення розміру вала з урахуванням знаків;

ES і EI верхнє і нижнє відхилення розміру отвору з урахуванням знаків.

Середнє значення дійсних відхилень вимірюваного розміру від його номіналу позначимо через . Величину зсуву від позначимо через Е. Тоді

(8)

На мал. 1 показані два крайніх положення кривої нормального розподілу

в полї допуску, коли зсув від координати середини полю чи допуску знаходиться в межах припустимих значень, і два інших крайніх положення кривої нормального розподілу, коли зміщено відносно на величину, що перевищує припустиме значення. У результаті цього виникає брак, тобто частина деталей q₁ і q₂ буде мати відхилення розмірів, що виходять за межі допуску.

На мал. 1,а видно, що допустима погрішність настроювання ріжучого інструмента на розмір дорівнює

(9)

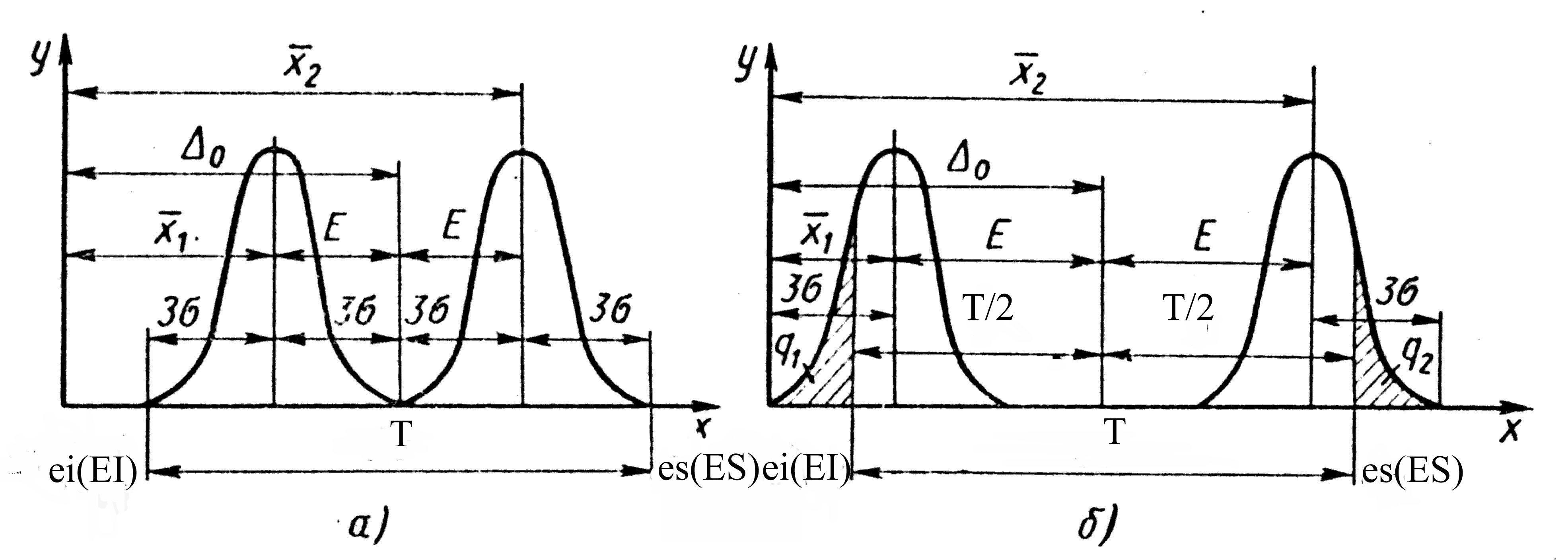
Мал.1. Припустимі (а) і неприпустимі (б) зсуви центра розсіювання погрішностей

Фактична величина погрішності настроювання визначиться

за формулою: (10).

Для роботи без браку повинна бути дотримана нерівність

(11)

Якщо ця нерівність дотримана не буде і , то при обробці настроєної партії неминучий брак навіть при надлишковій точності процесу. Ймовірний відсоток цього браку (мал. 1.1, б) можна визначити по формулі

(12)

Для порівняльної оцінки точності аналогічних операцій можна користатися коефіцієнтом точності Кт: (13)

При К_т1 точність процесу достатня, а при К_т>1 недостатня.

Для оцінки точності настроювання верстату користаються коефіцієнтом точності настроювання е: . (14)

При цьому припустиме значення е_д : (15) . Фактичне значення е_ф визначиться за формулю:

. (16)

Умови роботи без браку обмежуються нерівностями:

(17)

Для оцінки стійкості процесу за великою вибіркою досить підтверджень гіпотез нормальності і випадковісті вибірки. Якщо ці гіпотези підтверджуються, то процес можна вважати стійким у часі.

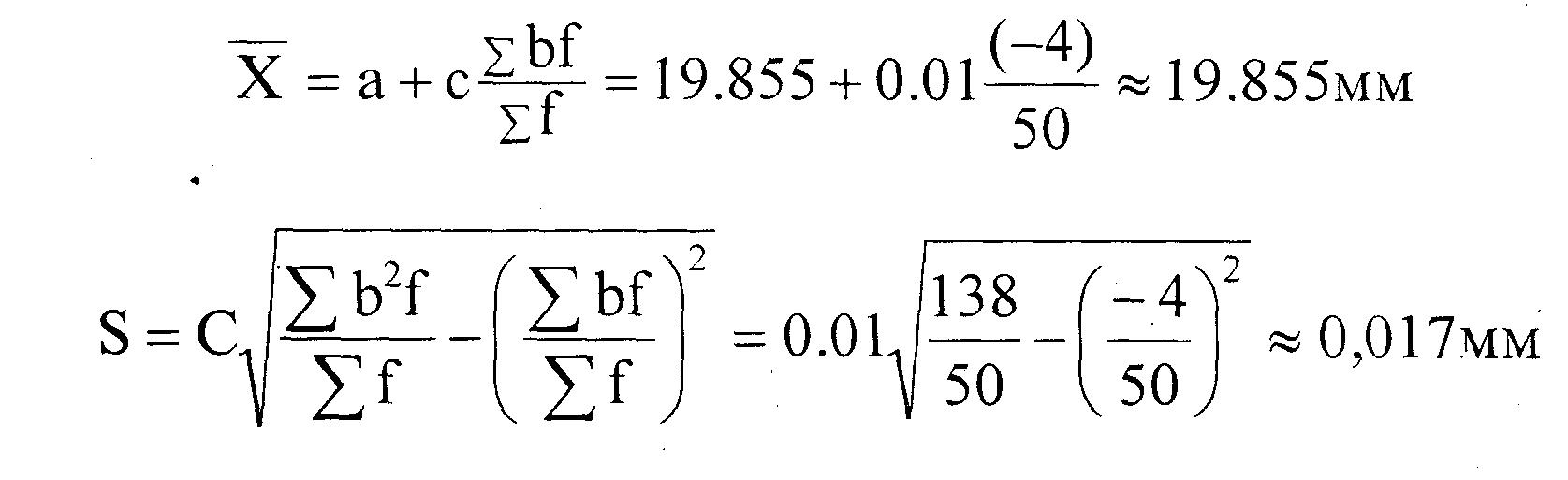
Зробимо перевірку гіпотези випадковості вибірки за методом послідовних різностей. Для цього з кожного наступного значення розміру деталі (табл.1,2 ), починаючи з другого, віднімемо попередній розмір і, таким чином, складемо 49 різностей. Наприклад,

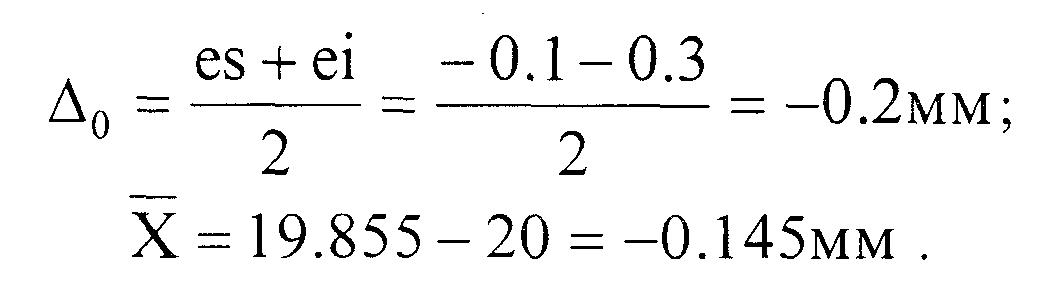
Фактичний зсув центра розсіювання відносно дорівнює

Таблиця 1. - Результати вимірів діаметра роликів.

Но- мер роли-ика	D,мм	Но-мер роли- ка	D,мм	Но-мер роли-ка	D,мм	Но-мер роли-ка	D,мм	Но-мер роли-ка	D,мм
1	19,86	11	19,82	21	19,82	31	19,85	41	19,83
2	19,83	12	19,84	22	19,85	32	19,84	42	19,84
3	19,84	13	19,84	23	19,84	33	19,85	43	19,85
4	19,85	14	19,87	24	19,81	34	19,86	44	19,87
5	19,86	15	19,88	25	19,88	35	19,87	45	19,89
6	19,83	16	19,83	26	19,85	36	19,82	46	19,85
7	19,84	17	19,84	27	19,84	37	19,83	47	19,84
8	19,85	18	19,85	28	19,85	38	19,84	48	19,85
9	19,86	19	19,86	29	19,86	39	19,85	49	19,86
10	19,86	20	19,86	30	19,87	40	19,86	50	19,87

Таблиця 2 - Розподіл розмірів роликів.

Розряди	Середина розряду Xi	f		bf	b2f	Примітка
19,81 - 19,82	19,815	1	-4	-4	16	а = 19,855мм с = 0,01мм
19,82 - 19,83	19,825	3	-3	-9	27
19,83 - 19,84	19,835	5	-2	-10	20
19,84 - 19,85	19,845	11	-1	-11	11
19,85 - 19,86	19,855	12	0	0	0
19,86 - 19,87	19,865	10	1	10	10
19,87 - 19,88	19,875	5	2	10	20
19,88 - 19,89	19,885	2	3	6	18
19,89 - 19,90	19,895	1	4	4	16
		50		-4	138

За даними табл. 2 обчислимо статистичні характеристики отриманого емпіричного розподілу:

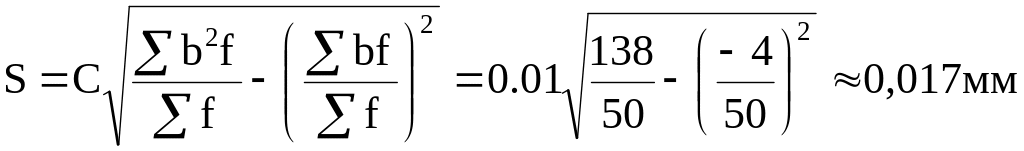
Потім зробимо перевірку гіпотези випадковості вибірки по методу послідовних різностей. Для цього з кожного наступного значення розміру деталі по табл.1, починаючи з другого, віднімемо попередній розмір і, таким чином, складемо 49 різностей. Наприклад,

a₁ = 19.83 - 19.86 = -0.03; a₂ = 19.84 - 19.83 = 0.01 і т.д.

Результати обчислень приведені нижче:

a1

=

-0.03

a11

=

0.02

a21

=

0.03

a31

=

-0.01

a41

=

0.01

a2

=

0.01

a12

=

0.00

a22

=

-0.01

a32

=

0.01

a42

=

0.01

a3

=

0.01

a13

=

0.03

a23

=

-0.03

a33

=

0.01

a43

=

0.02

a4

=

0.01

a14

=

0.01

a24

=

0.07

a34

=

0.01

a44

=

0.02

a5

=

-0.03

a15

=

-0.05

a25

=

-0.03

a35

=

-0.05

a45

=

-0.04

a6

=

0.01

a16

=

0.01

a26

=

-0.01

a36

=

0.01

a46

=

-0.01

a7

=

0.01

a17

=

0.01

a27

=

0.01

a37

=

0.01

a47

=

0.01

a8

=

0.01

a18

=

0.01

a28

=

0.01

a38

=

0.01

a48

=

0.01

a9

=

0.00

a19

=

0.00

a29

=

0.01

a39

=

0.01

a49

=

0.01

a10

=

-0.04

a20

=

-0.04

a30

=

-0.02

a40

=

-0.03

Ці різниці необхідно звести в квадрат і підсумовувати для обчислення величини C ² :

Для зручності обчислення зробимо угруповання абсолютних значень і підрахуємо іх частоти:

a_{ί ……………0 0.01 0.02 0.03 0.04 0.05 0.07}

f _{ί ……………3 29 4 7 3 2 1}

Величина критерію τ буде дорівнює

Критична область τ при ймовірності α=0.95 дорівнює

Значення τ визначається зі співвідношення q/100=0.5- Ф(t_q ), відкіля допусти-

мий зсув центра розсіювання (допуск на настроювання) дорівнює Ф(t_q )=0.5-q/100.

Знаючи Ф(t_q ), по таблиці 1 додатку можна визначити t_q. Наприклад, n = 50 при q = 5%, Ф(t_q ) =0.5 – 5/100 =0.45. По таблиці 1 додатку цьому значенню функції відповідає t_q = 1.65.

Тому що τ > τ_q, гіпотеза випадковості вибірки підтверджується, тобто в період відбору проби не було зсуву центра розсіювання погрішностей обробки.

Тепер зробимо перевірку гіпотези нормальності розподілу сукупності, з якого була узята вибірка. Для цього приймемо , і складемо допоміжну табл.3 для обчислення критерію λ.

Таблиця 3. - Допоміжні дані для обчислення λ

				f	N’x	Nx
19.815	2.36	0.0246	0.72	1	0.72	1	0.28
19.825	1.77	0.0833	2.45	3	3.17	4	0.83
19.835	1.18	0.1989	5.82	5	8.99	9	0.01
19.845	0.59	0.3352	9.85	11	18.84	20	1.16
19.855	0.00	0.3988	11.75	12	30.59	32	1.41
19.865	0.59	0.3352	9.85	10	40.44	42	1.58
19.875	1.18	0.1989	5.82	5	46.26	47	0.74
19.885	1.77	0.0833	2.45	2	48.70	49	0.30
19.895	2.36	0.0246	0.72	1	49.73	50	0.57

У таблиці величина t обчислена за формулою:

Значення Z_t узяті з таблиці 4 додатку.

Величина є постійної для всіх значень Z_t і дорівнює:

Критерій λ буде дорівнювати:

Цьому значенню λ (див.табл. 12 у додатку ) відповідає Р(λ) = 1, отже, гіпотеза нормальності розподілу підтверджується.

Сумарна погрішність буде дорівнює

Для обчислення визначимо σ:

Значення Z₂ узято з таблиці 19 додатку:

Постійні погрішності:

Отже, мм

Тому що T = 0.2мм і Δ > Т, процес не забезпечує необхідну точність.

Основною причиною цього явища служить неправильне настроювання верстата. За рахунок піднастроювання можна знизити постійну погрішність Δ_п. Координата середини полю допуску дорівнює:

;

.

Фактичний зсув центра розсіювання відносно Δ₀ дорівнює

.

Допустимий зсув центра розсіювання дорівнює

Тому що Е_ф>Е_д , те можливий відсоток браку

На мал. 2 графічно показане фактичне розсіювання розмірів у полі допуску.

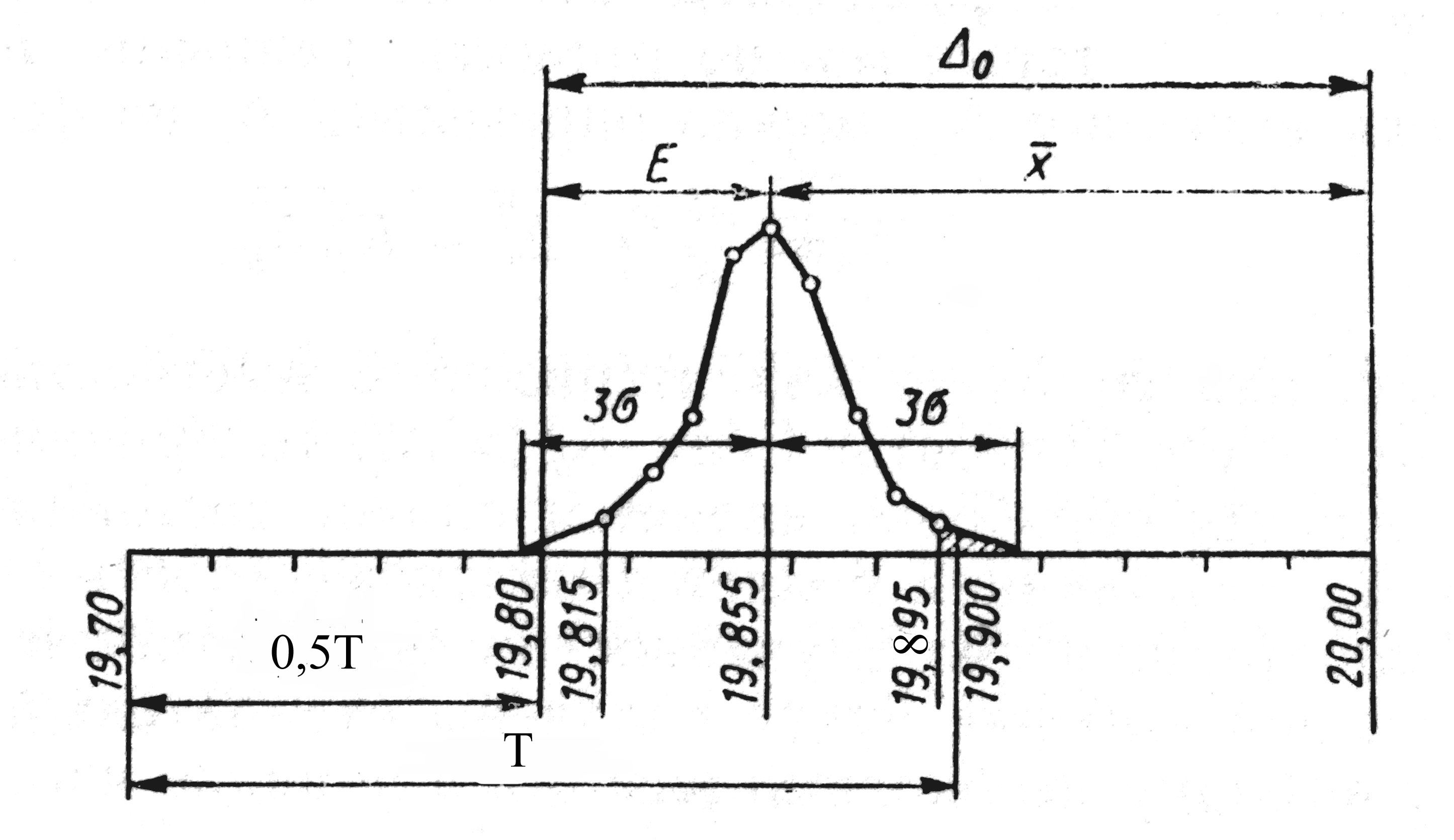
Мал.2 Крива розподілу розмірів роликів

Щоб уникнути появи шлюбу необхідно змінити настроювання так, щоб чи, прийнявши допуск на настроювання Т_н=0,037мм, тобто поклавши Δ_п=Т_н=0,037 мм, необхідно прагнути одержати при настроюванні

чи необхідно, щоб